人教版数学九年级上册 23.2中心对称同步测试试题(一)Word版含答案
文档属性
| 名称 | 人教版数学九年级上册 23.2中心对称同步测试试题(一)Word版含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 303.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览



文档简介
中心对称同步测试试题(一)
一.选择题
1.下列图标中,是中心对称图形的是( )
A.
B.
C.
D.
2.下列关于平行四边形的说法正确的是( )
①平行四边形既是轴对称图形也是中心对称图形;②平行四边行的对边相等,对角互补;③平行四边形的对角线互相平分;④平行四边形具有不稳定性;
A.①②③④
B.①③④
C.③④
D.①②③
3.下列是世界一些国家的国旗图案,其中是中心对称图形的是( )
A.
B.
C.
D.
4.以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q的坐标为( )
A.
C.
5.下列四个图形中,是中心对称图形的是( )
A.
B.
C.
D.
6.如图,已知△ABC和△A'B'C'关于点O成中心对称,则下列结论错误的是( )
A.∠ABC=∠A'B'C'
B.∠AOB=∠A'OB'
C.AB=A'B'
D.OA=OB'
7.如图,等边△OAB的边OB在x轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A'的坐标是( )
A.(﹣1,)
B.(,﹣1)
C.(﹣,1)
D.(﹣2,1)
8.点(﹣5,7)关于原点对称的点为( )
A.
C.
9.如图,点O是?ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是( )
A.
B.
C.
D.
10.如图,已知点A(2,1),B(0,2),将线段AB绕点M逆时针旋转到A1B1,点A与A1是对应点,则点M的坐标是( )
A.
C.
二.填空题
11.如图,直角坐标系中,已知点A(﹣3,0),B(0,4),将△AOB连续作旋转变换,依次得到三角形①,②,③,④,…则第19个三角形中顶点A的坐标是
.
12.平面直角坐标系中,点A的坐标为(,1),以原点O为中心,将点A逆时针旋转150o得到点A′,则点A′的坐标为
.
13.如图,两个“心”形有一个公共点O,且点C,O,E在同一条直线上,OC=OE=OD,下列说法中:
①这两个“心”形关于点O成中心对称;
②点C,E是以点O为对称中心的一对对称点;
③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB;
④若把这两个“心”形看作一个整体,则它又是一个中心对称图形.
正确的有
.(只填你认为正确的说法的序号)
14.在平面直角坐标系中,△OAB的位置如图所示,将△OAB绕点O顺时针旋转90°得△OA1B1;再将△OA1B1绕点O顺时针旋转90°得△OA2B2;再将△OA2B2绕点O顺时针旋转90°得△OA3B3;……依此类推,第2020次旋转得到△OA2020B2020,则项点A的对应点A2020的坐标是
.
15.在平面直角坐标系中,正方形5n的顶点坐标分别为A(1,1),B(1,﹣1),C(﹣1,﹣1),D(﹣1,1),y轴上有一点P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,……,按此操作下去,则P2020的坐标为
.
三.解答题
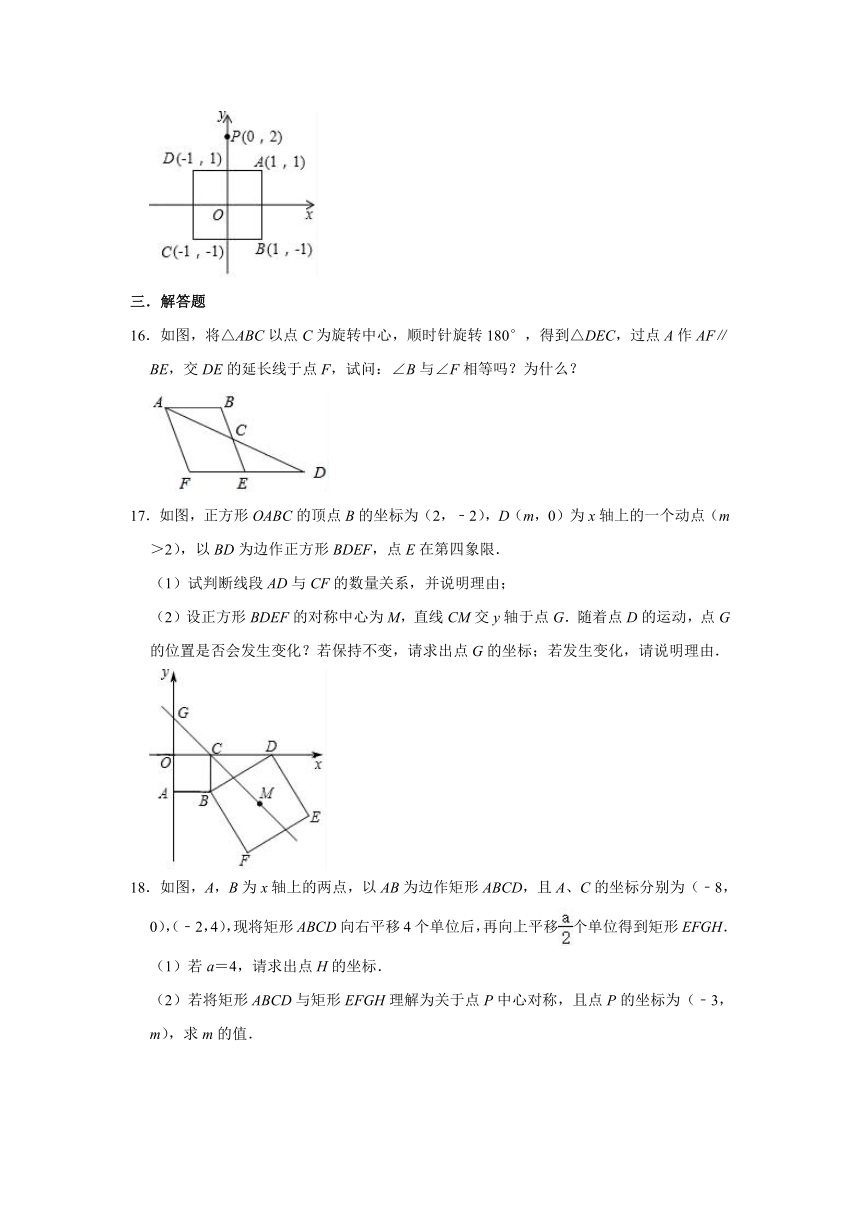
16.如图,将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,过点A作AF∥BE,交DE的延长线于点F,试问:∠B与∠F相等吗?为什么?
17.如图,正方形OABC的顶点B的坐标为(2,﹣2),D(m,0)为x轴上的一个动点(m>2),以BD为边作正方形BDEF,点E在第四象限.
(1)试判断线段AD与CF的数量关系,并说明理由;
(2)设正方形BDEF的对称中心为M,直线CM交y轴于点G.随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.
18.如图,A,B为x轴上的两点,以AB为边作矩形ABCD,且A、C的坐标分别为(﹣8,0),(﹣2,4),现将矩形ABCD向右平移4个单位后,再向上平移个单位得到矩形EFGH.
(1)若a=4,请求出点H的坐标.
(2)若将矩形ABCD与矩形EFGH理解为关于点P中心对称,且点P的坐标为(﹣3,m),求m的值.
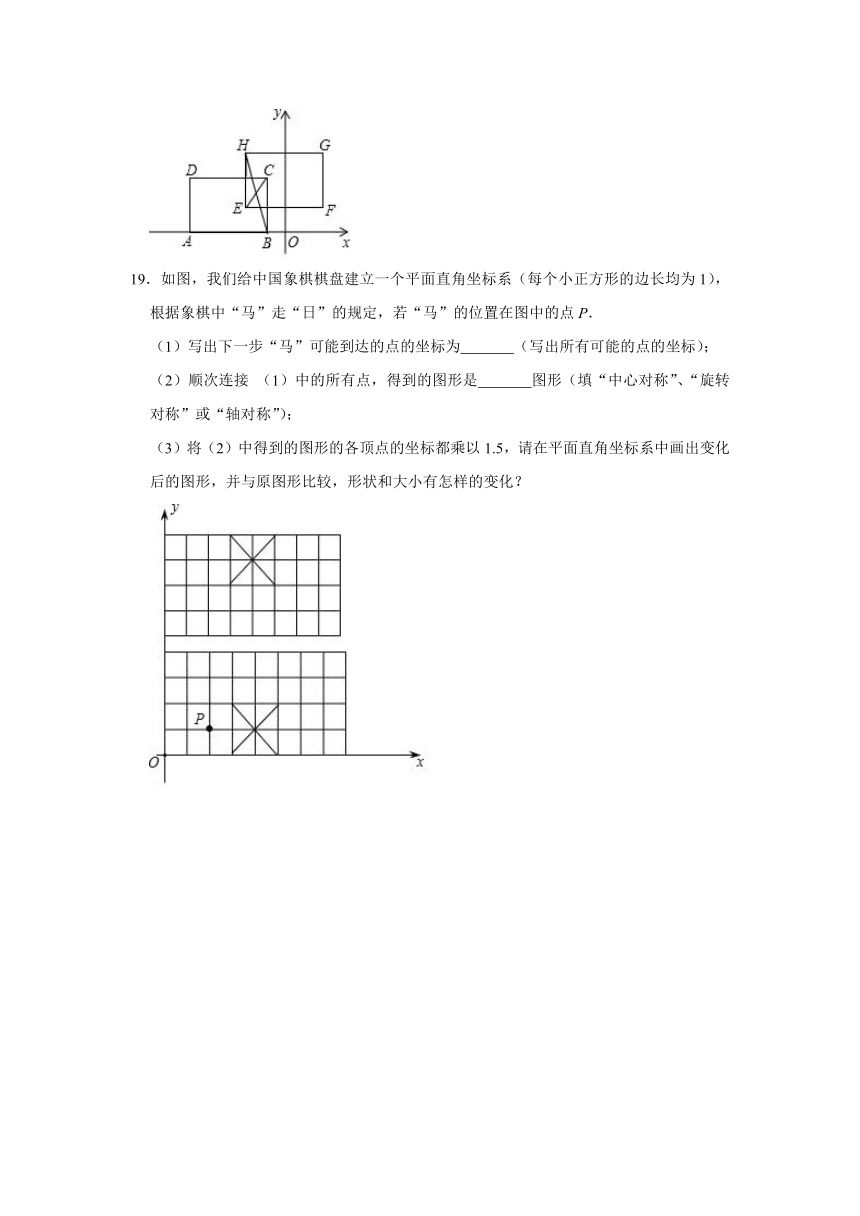
19.如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标为
(写出所有可能的点的坐标);
(2)顺次连接
(1)中的所有点,得到的图形是
图形(填“中心对称”、“旋转对称”或“轴对称”);
(3)将(2)中得到的图形的各顶点的坐标都乘以1.5,请在平面直角坐标系中画出变化后的图形,并与原图形比较,形状和大小有怎样的变化?
参考答案与试题解析
一.选择题
1.【解答】解:A、不属于中心对称图形;
B、属于中心对称图形;
C、不属于中心对称图形;
D、不属于中心对称图形;
故选:B.
2.【解答】解:①平行四边形不是轴对称图形,是中心对称图形,故原说法错误;
②平行四边行的对边相等,对角相等,故原说法错误;
③平行四边形的对角线互相平分,说法正确;
④平行四边形具有不稳定性,说法正确.
故选:C.
3.【解答】解:A.不是中心对称图形,故本选项不合题意;
B.不是中心对称图形,故本选项不合题意;
C.是中心对称图形,故本选项符合题意.
D.不是中心对称图形,故本选项不合题意;
故选:C.
4.【解答】解:如图所示,建立平面直角坐标系,点Q的坐标为(﹣5,4).
故选:C.
5.【解答】解:A、不是中心对称图形,故此选项不合题意;
B、不是中心对称图形,故此选项不合题意;
C、是中心对称图形,故此选项符合题意;
D、不是中心对称图形,故此选项不合题意;
故选:C.
6.【解答】解:∵△ABC和△A′B′C′关于点O成中心对称,
∴△ABC≌△A′B′C′,
∴AB=A′B′,OA=OA′,∠ABC=∠A′B′C′,
可得∠AOC=∠A′OC′,
故A,B,C正确,只有D选项错误.
故选:D.
7.【解答】解:如图,过点A作AE⊥OB于E,过点A′作A′H⊥x轴于H.
∵B(2,0),△AOB是等边三角形,
∴OA=OB=AB=2,
∵AE⊥OB,
∴OE=EB=1,
∴AE==,
∵A′H⊥OH,
∴∠A′HO=∠AEO=∠AOA′=90°,
∴∠A′OH+∠AOE=90°,∠AOE+∠OAE=90°,
∴∠A′OH=∠OAE,
∴△A′OH≌△OAE(AAS),
∴A′H=OE=1,OH=AE=,
∴A′(﹣,1),
故选:C.
8.【解答】解:点(﹣5,7)关于原点对称的点为(5,﹣7).
故选:B.
9.【解答】解:如图,连接OA,OB,OC.设平行四边形的面积为4s.
∵点O是平行四边形ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD=s,
∵EF=AB,GH=BC,
∴S1=s,S2=s,
∴==,
故选:B.
10.【解答】解:如图,点M的坐标是(1,﹣1),
故选:B.
二.填空题
11.【解答】解:∵A(﹣4,0),B(0,3),
∴OA=4,OB=3,
∴AB==5,
∵△AOB连续作三次旋转变换回到原来的状态,
而19=3×6+1,
∴第19个三角形的状态与第1个一样,
∴第19个三角形中顶点A的横坐标为6×12=72,纵坐标是4,
即第19个三角形中顶点A的坐标是(72,4).
故答案为(72,4).
12.【解答】解:如图,过点A作AE⊥x轴于E.
∵A(,1),
∴OE=,AE=1,
∴tan∠AOE==,
∴∠AOE=30°,
∴OA=OA′=2OE=2,
∵∠AOA′=150°,
∴点A′在x轴上,
∴A′(﹣2,0),
故答案为(﹣2,0).
13.【解答】解:①这两个“心”形关于点O成中心对称;说法正确;
②点C,E是以点O为对称中心的一对对称点;说法正确;
③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB;说法正确;
④若把这两个“心”形看作一个整体,则它又是一个中心对称图形.说法正确.
所以正确的有①②③④.
故答案为:①②③④.
14.【解答】解:将△OAB绕点O顺时针旋转90°得△OA1B1;此时,点A1的坐标为(2,﹣1);
再将△OA1B1绕点O顺时针旋转90°得△OA2B2;此时,点A2的坐标为(﹣1,2);
再将△OA2B2绕点O顺时针旋转90°得△OA3B3;此时,点A3的坐标为(﹣2,1);
再将△OA3B3绕点O顺时针旋转90°得△OA4B4;此时,点A4的坐标为(1,2);
∴每旋转4次一个循环,
∵2020÷4=505,
∴第2020次旋转得到△OA2020B2020,则顶点A的对应点A2020的坐标与点A4的坐标相同,为(1,2);
故答案为:(1,2).
15.【解答】解:由题意P1(2,0),P2(0,﹣2),P3(﹣2,0),P4(0,2),P5(2,0),…P5与P1重合,从P5开始出现循环,
2020÷4=505,
∴P2020与P4重合,
∴P2020(0,2).
故答案为(0,2).
三.解答题
16.【解答】解:∠B与∠F相等,理由如下:
∵将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,
∴∠B=∠DEC,
∵AF∥BE,
∴∠F=∠DEC,
∴∠B=∠F.
17.【解答】解:(1)结论:AD=CF.
理由:连接AD,CF.
∵四边形ABCO和四边形BDEF都是正方形,
∴AB=BC,BD=BF,∠ABC=∠FBD=90°,
∴∠ABD=∠FBD,
∴△ABD≌△CBF(SAS),
∴AD=CF.
(2)结论:点G的位置不发生变化.
理由:过点F作FH⊥CB交CB的延长线于点H.
∵∠BCD=∠DBF=∠H=90°,
∴∠CBD+∠FBH=90°,∠FBH+∠BFH=90°,
∴∠CBD=∠BFH,
∵BD=BF,
∴△BCD≌△FHB(AAS),
∴CD=BH=m﹣2,BC=FH=2,
∴F(4,﹣m),
又D(m,0),
∴M(2+,﹣),
作MN⊥x轴,在△CMN中,MN=,CN=,
∴△AMN是等腰直角三角形,
∴△OCG也是等腰直角三角形,
∴OG=OC=2,
∴G(0,2).
18.【解答】解:(1)∵点A(﹣8,0)向右平移4个单位后,再向上平移个单位得到点E,
∴点E的坐标为(﹣4,2),
∵点C(﹣2,4)向右平移4个单位后,再向上平移个单位得到点G,
∴点G的坐标为(2,6),
∴H点的坐标为(﹣4,6);
(2)连接AG、DF它们的交点为点P,如图,
由题意有A(﹣8,0),G(2,4+),
∴AG的中点P点坐标为(﹣3,2+),
∵P的坐标为(﹣3,m),
∴m=2+.
19.【解答】解:(1)下一步“马”可能到达的点的坐标:(0,0),(0,2),(1,3),(3,3),(4,2),(4,0)
一.选择题
1.下列图标中,是中心对称图形的是( )
A.
B.
C.
D.
2.下列关于平行四边形的说法正确的是( )
①平行四边形既是轴对称图形也是中心对称图形;②平行四边行的对边相等,对角互补;③平行四边形的对角线互相平分;④平行四边形具有不稳定性;
A.①②③④
B.①③④
C.③④
D.①②③
3.下列是世界一些国家的国旗图案,其中是中心对称图形的是( )
A.
B.
C.
D.
4.以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q的坐标为( )
A.
C.
5.下列四个图形中,是中心对称图形的是( )
A.
B.
C.
D.
6.如图,已知△ABC和△A'B'C'关于点O成中心对称,则下列结论错误的是( )
A.∠ABC=∠A'B'C'
B.∠AOB=∠A'OB'
C.AB=A'B'
D.OA=OB'
7.如图,等边△OAB的边OB在x轴上,点B坐标为(2,0),以点O为旋转中心,把△OAB逆时针旋转90°,则旋转后点A的对应点A'的坐标是( )
A.(﹣1,)
B.(,﹣1)
C.(﹣,1)
D.(﹣2,1)
8.点(﹣5,7)关于原点对称的点为( )
A.
C.
9.如图,点O是?ABCD的对称中心,AD>AB,E、F是AB边上的点,且EF=AB;G、H是BC边上的点,且GH=BC,若S1,S2分别表示△EOF和△GOH的面积,则S1与S2之间的等量关系是( )
A.
B.
C.
D.
10.如图,已知点A(2,1),B(0,2),将线段AB绕点M逆时针旋转到A1B1,点A与A1是对应点,则点M的坐标是( )
A.
C.
二.填空题
11.如图,直角坐标系中,已知点A(﹣3,0),B(0,4),将△AOB连续作旋转变换,依次得到三角形①,②,③,④,…则第19个三角形中顶点A的坐标是
.
12.平面直角坐标系中,点A的坐标为(,1),以原点O为中心,将点A逆时针旋转150o得到点A′,则点A′的坐标为
.
13.如图,两个“心”形有一个公共点O,且点C,O,E在同一条直线上,OC=OE=OD,下列说法中:
①这两个“心”形关于点O成中心对称;
②点C,E是以点O为对称中心的一对对称点;
③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB;
④若把这两个“心”形看作一个整体,则它又是一个中心对称图形.
正确的有
.(只填你认为正确的说法的序号)
14.在平面直角坐标系中,△OAB的位置如图所示,将△OAB绕点O顺时针旋转90°得△OA1B1;再将△OA1B1绕点O顺时针旋转90°得△OA2B2;再将△OA2B2绕点O顺时针旋转90°得△OA3B3;……依此类推,第2020次旋转得到△OA2020B2020,则项点A的对应点A2020的坐标是
.
15.在平面直角坐标系中,正方形5n的顶点坐标分别为A(1,1),B(1,﹣1),C(﹣1,﹣1),D(﹣1,1),y轴上有一点P(0,2).作点P关于点A的对称点P1,作点P1关于点B的对称点P2,作点P2关于点C的对称点P3,作点P3关于点D的对称点P4,作点P4关于点A的对称点P5,作点P5关于点B的对称点P6,……,按此操作下去,则P2020的坐标为
.
三.解答题
16.如图,将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,过点A作AF∥BE,交DE的延长线于点F,试问:∠B与∠F相等吗?为什么?
17.如图,正方形OABC的顶点B的坐标为(2,﹣2),D(m,0)为x轴上的一个动点(m>2),以BD为边作正方形BDEF,点E在第四象限.
(1)试判断线段AD与CF的数量关系,并说明理由;
(2)设正方形BDEF的对称中心为M,直线CM交y轴于点G.随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.
18.如图,A,B为x轴上的两点,以AB为边作矩形ABCD,且A、C的坐标分别为(﹣8,0),(﹣2,4),现将矩形ABCD向右平移4个单位后,再向上平移个单位得到矩形EFGH.
(1)若a=4,请求出点H的坐标.
(2)若将矩形ABCD与矩形EFGH理解为关于点P中心对称,且点P的坐标为(﹣3,m),求m的值.
19.如图,我们给中国象棋棋盘建立一个平面直角坐标系(每个小正方形的边长均为1),根据象棋中“马”走“日”的规定,若“马”的位置在图中的点P.
(1)写出下一步“马”可能到达的点的坐标为
(写出所有可能的点的坐标);
(2)顺次连接
(1)中的所有点,得到的图形是
图形(填“中心对称”、“旋转对称”或“轴对称”);
(3)将(2)中得到的图形的各顶点的坐标都乘以1.5,请在平面直角坐标系中画出变化后的图形,并与原图形比较,形状和大小有怎样的变化?
参考答案与试题解析
一.选择题
1.【解答】解:A、不属于中心对称图形;
B、属于中心对称图形;
C、不属于中心对称图形;
D、不属于中心对称图形;
故选:B.
2.【解答】解:①平行四边形不是轴对称图形,是中心对称图形,故原说法错误;
②平行四边行的对边相等,对角相等,故原说法错误;
③平行四边形的对角线互相平分,说法正确;
④平行四边形具有不稳定性,说法正确.
故选:C.
3.【解答】解:A.不是中心对称图形,故本选项不合题意;
B.不是中心对称图形,故本选项不合题意;
C.是中心对称图形,故本选项符合题意.
D.不是中心对称图形,故本选项不合题意;
故选:C.
4.【解答】解:如图所示,建立平面直角坐标系,点Q的坐标为(﹣5,4).
故选:C.
5.【解答】解:A、不是中心对称图形,故此选项不合题意;
B、不是中心对称图形,故此选项不合题意;
C、是中心对称图形,故此选项符合题意;
D、不是中心对称图形,故此选项不合题意;
故选:C.
6.【解答】解:∵△ABC和△A′B′C′关于点O成中心对称,
∴△ABC≌△A′B′C′,
∴AB=A′B′,OA=OA′,∠ABC=∠A′B′C′,
可得∠AOC=∠A′OC′,
故A,B,C正确,只有D选项错误.
故选:D.
7.【解答】解:如图,过点A作AE⊥OB于E,过点A′作A′H⊥x轴于H.
∵B(2,0),△AOB是等边三角形,
∴OA=OB=AB=2,
∵AE⊥OB,
∴OE=EB=1,
∴AE==,
∵A′H⊥OH,
∴∠A′HO=∠AEO=∠AOA′=90°,
∴∠A′OH+∠AOE=90°,∠AOE+∠OAE=90°,
∴∠A′OH=∠OAE,
∴△A′OH≌△OAE(AAS),
∴A′H=OE=1,OH=AE=,
∴A′(﹣,1),
故选:C.
8.【解答】解:点(﹣5,7)关于原点对称的点为(5,﹣7).
故选:B.
9.【解答】解:如图,连接OA,OB,OC.设平行四边形的面积为4s.
∵点O是平行四边形ABCD的对称中心,
∴S△AOB=S△BOC=S平行四边形ABCD=s,
∵EF=AB,GH=BC,
∴S1=s,S2=s,
∴==,
故选:B.
10.【解答】解:如图,点M的坐标是(1,﹣1),
故选:B.
二.填空题
11.【解答】解:∵A(﹣4,0),B(0,3),
∴OA=4,OB=3,
∴AB==5,
∵△AOB连续作三次旋转变换回到原来的状态,
而19=3×6+1,
∴第19个三角形的状态与第1个一样,
∴第19个三角形中顶点A的横坐标为6×12=72,纵坐标是4,
即第19个三角形中顶点A的坐标是(72,4).
故答案为(72,4).
12.【解答】解:如图,过点A作AE⊥x轴于E.
∵A(,1),
∴OE=,AE=1,
∴tan∠AOE==,
∴∠AOE=30°,
∴OA=OA′=2OE=2,
∵∠AOA′=150°,
∴点A′在x轴上,
∴A′(﹣2,0),
故答案为(﹣2,0).
13.【解答】解:①这两个“心”形关于点O成中心对称;说法正确;
②点C,E是以点O为对称中心的一对对称点;说法正确;
③这两个“心”形成轴对称,对称轴是过点O且与直线AB垂直的直线和直线AB;说法正确;
④若把这两个“心”形看作一个整体,则它又是一个中心对称图形.说法正确.
所以正确的有①②③④.
故答案为:①②③④.
14.【解答】解:将△OAB绕点O顺时针旋转90°得△OA1B1;此时,点A1的坐标为(2,﹣1);
再将△OA1B1绕点O顺时针旋转90°得△OA2B2;此时,点A2的坐标为(﹣1,2);
再将△OA2B2绕点O顺时针旋转90°得△OA3B3;此时,点A3的坐标为(﹣2,1);
再将△OA3B3绕点O顺时针旋转90°得△OA4B4;此时,点A4的坐标为(1,2);
∴每旋转4次一个循环,
∵2020÷4=505,
∴第2020次旋转得到△OA2020B2020,则顶点A的对应点A2020的坐标与点A4的坐标相同,为(1,2);
故答案为:(1,2).
15.【解答】解:由题意P1(2,0),P2(0,﹣2),P3(﹣2,0),P4(0,2),P5(2,0),…P5与P1重合,从P5开始出现循环,
2020÷4=505,
∴P2020与P4重合,
∴P2020(0,2).
故答案为(0,2).
三.解答题
16.【解答】解:∠B与∠F相等,理由如下:
∵将△ABC以点C为旋转中心,顺时针旋转180°,得到△DEC,
∴∠B=∠DEC,
∵AF∥BE,
∴∠F=∠DEC,
∴∠B=∠F.
17.【解答】解:(1)结论:AD=CF.
理由:连接AD,CF.
∵四边形ABCO和四边形BDEF都是正方形,
∴AB=BC,BD=BF,∠ABC=∠FBD=90°,
∴∠ABD=∠FBD,
∴△ABD≌△CBF(SAS),
∴AD=CF.
(2)结论:点G的位置不发生变化.
理由:过点F作FH⊥CB交CB的延长线于点H.
∵∠BCD=∠DBF=∠H=90°,
∴∠CBD+∠FBH=90°,∠FBH+∠BFH=90°,
∴∠CBD=∠BFH,
∵BD=BF,
∴△BCD≌△FHB(AAS),
∴CD=BH=m﹣2,BC=FH=2,
∴F(4,﹣m),
又D(m,0),
∴M(2+,﹣),
作MN⊥x轴,在△CMN中,MN=,CN=,
∴△AMN是等腰直角三角形,
∴△OCG也是等腰直角三角形,
∴OG=OC=2,
∴G(0,2).
18.【解答】解:(1)∵点A(﹣8,0)向右平移4个单位后,再向上平移个单位得到点E,
∴点E的坐标为(﹣4,2),
∵点C(﹣2,4)向右平移4个单位后,再向上平移个单位得到点G,
∴点G的坐标为(2,6),
∴H点的坐标为(﹣4,6);
(2)连接AG、DF它们的交点为点P,如图,
由题意有A(﹣8,0),G(2,4+),
∴AG的中点P点坐标为(﹣3,2+),
∵P的坐标为(﹣3,m),
∴m=2+.
19.【解答】解:(1)下一步“马”可能到达的点的坐标:(0,0),(0,2),(1,3),(3,3),(4,2),(4,0)
同课章节目录
