人教版数学九年级上册23.3课时学习 图案设计同步测试试题(一)Word版含答案
文档属性
| 名称 | 人教版数学九年级上册23.3课时学习 图案设计同步测试试题(一)Word版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览



文档简介
课时学习
图案设计同步测试试题(一)
一.选择题
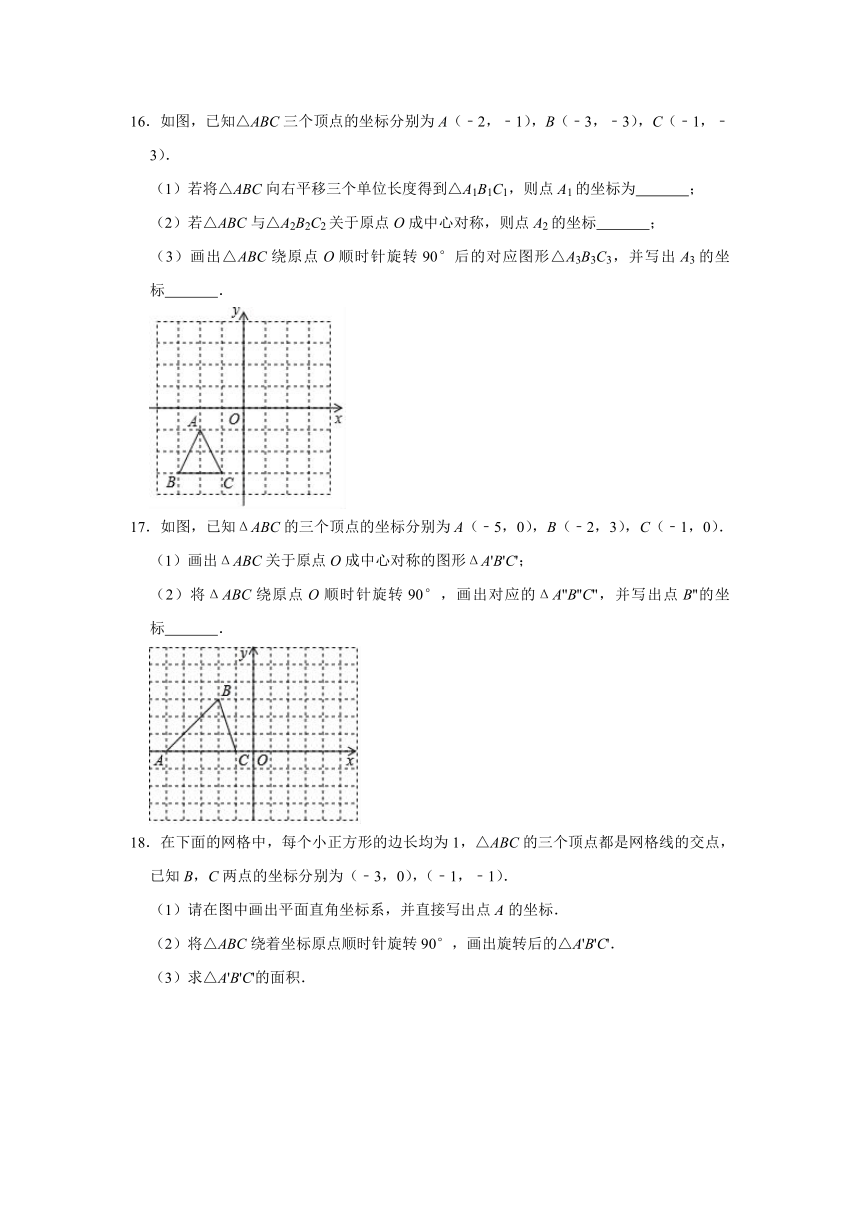
1.如图所示,北京2022年冬奥会会徽是以汉字“冬”为灵感设计的.下列四个选项中,由会徽经过平移而得到的是( )
A.
B.
C.
D.
2.下列图案中,含有旋转变换的有( )
A.4个
B.3个
C.2个
D.1个
3.在下列说法中,(1)角的对称轴是它的角平分线所在直线;(2)图形的平移、旋转、轴对称变换不改变图形的形状和大小;(3)三角形的三条高线一定在三角形内;(4)多边形的外角和是360°.则正确的有( )
A.4个
B.3个
C.2个
D.1个
4.将如图所示的图案平移后可以得到下图中的( )
A.
B.
C.
D.
5.如图,在4×4的网格纸中,△ABC的三个顶点都在格点上,现要在这张网格纸的四个格点M,N,P,Q中找一点作为旋转中心.将△ABC绕着这个中心进行旋转,旋转前后的两个三角形成中心对称,且旋转后的三角形的三个顶点都在这张4×4的网格纸的格点上,那么满足条件的旋转中心有( )
A.点M,点N
B.点M,点Q
C.点N,点P
D.点P,点Q
6.如图,平面内某正方形内有一长为10宽为5的矩形,它可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,则该正方形边长的最小整数n为( )
A.10
B.11
C.12
D.13
7.在下面四个图形中,不能通过平移其中一个四边形得到的是( )
A.
B.
C.
D.
8.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距的另一个格点的运动称为一次跳马变换.例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处,现有17×17的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是( )
A.11
B.12
C.13
D.14
9.如图,四边形ABCD是轴对称图形,对角线BD所在的直线是它的对称轴,∠A=∠C=90°,AB≠AD,若把这个轴对称图形沿对角线BD剪开成两个三角形后,再把这两个三角形的一边完全重合在一起,重新拼成一个中心对称图形,则拼法共有( )
A.0种
B.1种
C.2种
D.3种
10.如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )
A.折叠后∠ABE
和∠CBD
一定相等
B.△EBD
是等腰三角形,EB=ED
C.折叠后得到的整个图形是轴对称图形
D.△EBA
和△EDC
一定是全等三角形
二.填空题
11.如图,在4×4的正方形网格中,已有4个小方格涂成了灰色,现在要从其余白色小方格中选出一个也涂成灰色,使整个灰色部分的图形构成轴对称图形,这样的白色小方格
个.
12.如图,在等边三角形网格中,已有两个小等边三角形被涂黑,若再将图中其余小等边三角形涂黑一个,使涂色部分构成一个轴对称图形,则有种不同
的涂法.
13.如图,在△OAB中,∠1=∠2.将△OAB绕点O顺时针旋转180°,点A的对应点记为C,点B的对应点记为D,顺次连接BC,CD,DA得到四边形ABCD.
(1)补全图形;
(2)所得四边形ABCD为
(从①矩形;②菱形;③正方形中选择,只填写序号即可),判断此结论的依据是
.
14.在平面直角坐标系中,点P(x,y)经过某种变换后得到点P′(﹣y+1,x+2),我们把点P′(﹣y+1,x+2)叫做点P(x,y)的终结点.已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1,P2,P3,P4,…,Pn.若点P1的坐标为(2,0),则点P2020的坐标为
.
15.如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均在格点上.
(1)边AC的长等于
.
(2)以点C为旋转中心,把△ABC顺时针旋转,得到△A'B'C',使点B的对应点B'恰好落在边AC上,请在如图所示的网格中,用无刻度的直尺,作出旋转后的图形,并简要说明作图的方法(不要求证明).
三.解答题
16.如图,已知△ABC三个顶点的坐标分别为A(﹣2,﹣1),B(﹣3,﹣3),C(﹣1,﹣3).
(1)若将△ABC向右平移三个单位长度得到△A1B1C1,则点A1的坐标为
;
(2)若△ABC与△A2B2C2关于原点O成中心对称,则点A2的坐标
;
(3)画出△ABC绕原点O顺时针旋转90°后的对应图形△A3B3C3,并写出A3的坐标
.
17.如图,已知ΔABC的三个顶点的坐标分别为A(﹣5,0),B(﹣2,3),C(﹣1,0).
(1)画出ΔABC关于原点O成中心对称的图形ΔA'B'C';
(2)将ΔABC绕原点O顺时针旋转90°,画出对应的ΔA''B''C'',并写出点B''的坐标
.
18.在下面的网格中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(﹣3,0),(﹣1,﹣1).
(1)请在图中画出平面直角坐标系,并直接写出点A的坐标.
(2)将△ABC绕着坐标原点顺时针旋转90°,画出旋转后的△A'B'C'.
(3)求△A'B'C'的面积.
19.图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形边长为1,点A、B、C、D、E、F均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中以线段AB为边画个中心对称四边形ABGH,使其面积为9;
(2)在图②中以线段CD为边画一个轴对称四边形CDMN,使其面积为10;
(3)在图③中以线段EF为边画一个四边形EFPQ,使其满足仅有一对对角都为直角.
参考答案与试题解析
一.选择题
1.【解答】解:根据“平移”的定义可知,由题图经过平移得到的图形是:
.
故选:C.
2.【解答】解:根据旋转的含义可知:选项中给出的4个图都可以通过旋转得到,
故选:A.
3.【解答】解:角的对称轴是它的角平分线所在直线,所以(1)的说法正确;
图形的平移、旋转、轴对称变换不改变图形的形状和大小,所以(2)的说法正确;
锐角三角形的三条高线一定在三角形内,所以(3)的说法错误;
多边形的外角和是360°,所以(4)的说法正确.
故选:B.
4.【解答】解:观察各选项图形可知,B选项的图案可以通过原图形平移得到.
故选:B.
5.【解答】解:观察图象可知,点P.点N满足条件.
故选:C.
6.【解答】解:∵矩形长为10宽为5,
∴矩形的对角线长为:==5,
∵矩形在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,
∴该正方形的边长不小于5,
∵11<5<12,
∴该正方形边长的最小正数n为12.
故选:C.
7.【解答】解:选项A,B,C是可以通过平移其中一个四边形得到的,属于平移变换,选项D是通过旋转其中一个四边形得到的,是旋转变换.
故选:D.
8.【解答】解:根据题意可知:
如图所示:有17×17的正方形网格图形,根据“马走日”的变化方式,
按M﹣A﹣D﹣F的方向连续变换4次,
然后再同样的方式变换,连续变换12次到顶点N.
即经过4×3=12(次),
可从该正方形的顶点M经过跳马变换到达与其相对的顶点N,
所以最少需要跳马变换的次数是12次.
故选:B.
9.【解答】解:如图所示:3种拼法都是中心对称图形.
故选:D.
10.【解答】解:∵四边形ABCD为矩形,
∴∠A=∠C,AB=CD,AD∥BF,
在△EBA
和△EDC
中
,
∴△AEB≌△CED(AAS)(故D选项正确,不合题意)
∴BE=DE,△EBD是等腰三角形(故B选项正确,不合题意),
无法得到∠ABE=∠CBD(故A选项不正确,符合题意)
∴过E作BD边的中垂线,即是图形的对称轴.(故C选项正确,不合题意)
故选:A.
二.填空题
11.【解答】解:如图所示:当将1,2,3处涂灰色可以使整个灰色部分的图形构成轴对称图形,故共3个.
故答案为:3.
12.【解答】解:如图所示:当将1,2,3涂成黑色可以构成一个轴对称图形,
故有种不同3的涂法.
故答案为:3.
13.【解答】解:(1)如图,四边形ABCD即为所求.
(2)结论:四边形ABCD是矩形.
理由:∵∠1=∠2,
∴OA=OB,
由旋转的性质知OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵AC=2OA,BD=2OB,OA=OB,
∴AC=BD,
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形).
故答案为:①,对角线相等的平行四边形是矩形,
14.【解答】解:根据题意得点P1的坐标为(2,0),则点P2的坐标为(1,4),点P3的坐标为(﹣3,3),点P4的坐标为(﹣2,﹣1),点P5的坐标为(2,0),…,
而2020=4×505,
所以点P2020的坐标与点P4的坐标相同,为(﹣2,﹣1).
故答案为:(﹣2,﹣1).
15.【解答】解:(1)根据网格可知:
AB=4,BC=3,
∴AC==5,
故答案为:5;
(2)取格点E,F,M,N,作直线EF,直线MN,
MN与EF交于点A′,
EF与AC交于点B′,
连接CA′.
△A'B'C即为所求.
三.解答题
16.【解答】解:(1)如图,△A1B1C1,点A1的坐标为(1,﹣1);
(2)如图,△A2B2C2为所作,点A2的坐标为(2,1);
(3)如图,△A3B3C3为所作,点A3的坐标为(﹣1,2).
图案设计同步测试试题(一)
一.选择题
1.如图所示,北京2022年冬奥会会徽是以汉字“冬”为灵感设计的.下列四个选项中,由会徽经过平移而得到的是( )
A.
B.
C.
D.
2.下列图案中,含有旋转变换的有( )
A.4个
B.3个
C.2个
D.1个
3.在下列说法中,(1)角的对称轴是它的角平分线所在直线;(2)图形的平移、旋转、轴对称变换不改变图形的形状和大小;(3)三角形的三条高线一定在三角形内;(4)多边形的外角和是360°.则正确的有( )
A.4个
B.3个
C.2个
D.1个
4.将如图所示的图案平移后可以得到下图中的( )
A.
B.
C.
D.
5.如图,在4×4的网格纸中,△ABC的三个顶点都在格点上,现要在这张网格纸的四个格点M,N,P,Q中找一点作为旋转中心.将△ABC绕着这个中心进行旋转,旋转前后的两个三角形成中心对称,且旋转后的三角形的三个顶点都在这张4×4的网格纸的格点上,那么满足条件的旋转中心有( )
A.点M,点N
B.点M,点Q
C.点N,点P
D.点P,点Q
6.如图,平面内某正方形内有一长为10宽为5的矩形,它可以在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,则该正方形边长的最小整数n为( )
A.10
B.11
C.12
D.13
7.在下面四个图形中,不能通过平移其中一个四边形得到的是( )
A.
B.
C.
D.
8.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距的另一个格点的运动称为一次跳马变换.例如,在4×4的正方形网格图形中(如图1),从点A经过一次跳马变换可以到达点B,C,D,E等处,现有17×17的正方形网格图形(如图2),则从该正方形的顶点M经过跳马变换到达与其相对的顶点N,最少需要跳马变换的次数是( )
A.11
B.12
C.13
D.14
9.如图,四边形ABCD是轴对称图形,对角线BD所在的直线是它的对称轴,∠A=∠C=90°,AB≠AD,若把这个轴对称图形沿对角线BD剪开成两个三角形后,再把这两个三角形的一边完全重合在一起,重新拼成一个中心对称图形,则拼法共有( )
A.0种
B.1种
C.2种
D.3种
10.如图,把矩形纸片ABCD沿对角线折叠,设重叠部分为△EBD,那么下列说法错误的是( )
A.折叠后∠ABE
和∠CBD
一定相等
B.△EBD
是等腰三角形,EB=ED
C.折叠后得到的整个图形是轴对称图形
D.△EBA
和△EDC
一定是全等三角形
二.填空题
11.如图,在4×4的正方形网格中,已有4个小方格涂成了灰色,现在要从其余白色小方格中选出一个也涂成灰色,使整个灰色部分的图形构成轴对称图形,这样的白色小方格
个.
12.如图,在等边三角形网格中,已有两个小等边三角形被涂黑,若再将图中其余小等边三角形涂黑一个,使涂色部分构成一个轴对称图形,则有种不同
的涂法.
13.如图,在△OAB中,∠1=∠2.将△OAB绕点O顺时针旋转180°,点A的对应点记为C,点B的对应点记为D,顺次连接BC,CD,DA得到四边形ABCD.
(1)补全图形;
(2)所得四边形ABCD为
(从①矩形;②菱形;③正方形中选择,只填写序号即可),判断此结论的依据是
.
14.在平面直角坐标系中,点P(x,y)经过某种变换后得到点P′(﹣y+1,x+2),我们把点P′(﹣y+1,x+2)叫做点P(x,y)的终结点.已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1,P2,P3,P4,…,Pn.若点P1的坐标为(2,0),则点P2020的坐标为
.
15.如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均在格点上.
(1)边AC的长等于
.
(2)以点C为旋转中心,把△ABC顺时针旋转,得到△A'B'C',使点B的对应点B'恰好落在边AC上,请在如图所示的网格中,用无刻度的直尺,作出旋转后的图形,并简要说明作图的方法(不要求证明).
三.解答题
16.如图,已知△ABC三个顶点的坐标分别为A(﹣2,﹣1),B(﹣3,﹣3),C(﹣1,﹣3).
(1)若将△ABC向右平移三个单位长度得到△A1B1C1,则点A1的坐标为
;
(2)若△ABC与△A2B2C2关于原点O成中心对称,则点A2的坐标
;
(3)画出△ABC绕原点O顺时针旋转90°后的对应图形△A3B3C3,并写出A3的坐标
.
17.如图,已知ΔABC的三个顶点的坐标分别为A(﹣5,0),B(﹣2,3),C(﹣1,0).
(1)画出ΔABC关于原点O成中心对称的图形ΔA'B'C';
(2)将ΔABC绕原点O顺时针旋转90°,画出对应的ΔA''B''C'',并写出点B''的坐标
.
18.在下面的网格中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(﹣3,0),(﹣1,﹣1).
(1)请在图中画出平面直角坐标系,并直接写出点A的坐标.
(2)将△ABC绕着坐标原点顺时针旋转90°,画出旋转后的△A'B'C'.
(3)求△A'B'C'的面积.
19.图①、图②、图③均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形边长为1,点A、B、C、D、E、F均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
(1)在图①中以线段AB为边画个中心对称四边形ABGH,使其面积为9;
(2)在图②中以线段CD为边画一个轴对称四边形CDMN,使其面积为10;
(3)在图③中以线段EF为边画一个四边形EFPQ,使其满足仅有一对对角都为直角.
参考答案与试题解析
一.选择题
1.【解答】解:根据“平移”的定义可知,由题图经过平移得到的图形是:
.
故选:C.
2.【解答】解:根据旋转的含义可知:选项中给出的4个图都可以通过旋转得到,
故选:A.
3.【解答】解:角的对称轴是它的角平分线所在直线,所以(1)的说法正确;
图形的平移、旋转、轴对称变换不改变图形的形状和大小,所以(2)的说法正确;
锐角三角形的三条高线一定在三角形内,所以(3)的说法错误;
多边形的外角和是360°,所以(4)的说法正确.
故选:B.
4.【解答】解:观察各选项图形可知,B选项的图案可以通过原图形平移得到.
故选:B.
5.【解答】解:观察图象可知,点P.点N满足条件.
故选:C.
6.【解答】解:∵矩形长为10宽为5,
∴矩形的对角线长为:==5,
∵矩形在该正方形的内部及边界通过平移或旋转的方式,自由地从横放变换到竖放,
∴该正方形的边长不小于5,
∵11<5<12,
∴该正方形边长的最小正数n为12.
故选:C.
7.【解答】解:选项A,B,C是可以通过平移其中一个四边形得到的,属于平移变换,选项D是通过旋转其中一个四边形得到的,是旋转变换.
故选:D.
8.【解答】解:根据题意可知:
如图所示:有17×17的正方形网格图形,根据“马走日”的变化方式,
按M﹣A﹣D﹣F的方向连续变换4次,
然后再同样的方式变换,连续变换12次到顶点N.
即经过4×3=12(次),
可从该正方形的顶点M经过跳马变换到达与其相对的顶点N,
所以最少需要跳马变换的次数是12次.
故选:B.
9.【解答】解:如图所示:3种拼法都是中心对称图形.
故选:D.
10.【解答】解:∵四边形ABCD为矩形,
∴∠A=∠C,AB=CD,AD∥BF,
在△EBA
和△EDC
中
,
∴△AEB≌△CED(AAS)(故D选项正确,不合题意)
∴BE=DE,△EBD是等腰三角形(故B选项正确,不合题意),
无法得到∠ABE=∠CBD(故A选项不正确,符合题意)
∴过E作BD边的中垂线,即是图形的对称轴.(故C选项正确,不合题意)
故选:A.
二.填空题
11.【解答】解:如图所示:当将1,2,3处涂灰色可以使整个灰色部分的图形构成轴对称图形,故共3个.
故答案为:3.
12.【解答】解:如图所示:当将1,2,3涂成黑色可以构成一个轴对称图形,
故有种不同3的涂法.
故答案为:3.
13.【解答】解:(1)如图,四边形ABCD即为所求.
(2)结论:四边形ABCD是矩形.
理由:∵∠1=∠2,
∴OA=OB,
由旋转的性质知OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵AC=2OA,BD=2OB,OA=OB,
∴AC=BD,
∴四边形ABCD是矩形(对角线相等的平行四边形是矩形).
故答案为:①,对角线相等的平行四边形是矩形,
14.【解答】解:根据题意得点P1的坐标为(2,0),则点P2的坐标为(1,4),点P3的坐标为(﹣3,3),点P4的坐标为(﹣2,﹣1),点P5的坐标为(2,0),…,
而2020=4×505,
所以点P2020的坐标与点P4的坐标相同,为(﹣2,﹣1).
故答案为:(﹣2,﹣1).
15.【解答】解:(1)根据网格可知:
AB=4,BC=3,
∴AC==5,
故答案为:5;
(2)取格点E,F,M,N,作直线EF,直线MN,
MN与EF交于点A′,
EF与AC交于点B′,
连接CA′.
△A'B'C即为所求.
三.解答题
16.【解答】解:(1)如图,△A1B1C1,点A1的坐标为(1,﹣1);
(2)如图,△A2B2C2为所作,点A2的坐标为(2,1);
(3)如图,△A3B3C3为所作,点A3的坐标为(﹣1,2).
同课章节目录
