北师大版七年级数学上册第四单元《基本平面图形》单元练习题(Word版 含答案)
文档属性
| 名称 | 北师大版七年级数学上册第四单元《基本平面图形》单元练习题(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 335.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-02 23:40:59 | ||
图片预览


文档简介
北师大版七年级数学上册第四单元《基本平面图形》单元练习题(含答案)
一、单选题
1.下面四个图形中,是多边形的是( )
A. B. C. D.
2.多边形的一个顶点处的所有对角线把多边形分成了11个三角形,则经过这一点的对角线的条数是(?? )
A.8 B.9 C.10 D.11
3.已知线段AB=8cm,在直线AB上画BC,使BC=2cm,则线段AC的长度是( )
A.6cm B.10cm C.6cm或10cm D.4cm或16cm
4.已知在同一平面内但不在同一条直线上的三点、、,画直线,画射线,连接.按照上述语句,画图正确的是( )
A.B. C. D.
5.植树时,为了使同一行树坑在一条直线上,只需定出两个树坑的位置,其中的数学道理是( )
A.两点之间线段最短
B.两点之间直线最短
C.两点确定一条射线
D.两点确定一条直线
6.如图,由A测B,方向是:
A.南偏东32 B.南偏东58 C.北偏西32 D.北偏西58
7.下列说法中正确的是( )
A.两点之间的所有连线中,线段最短
B.射线就是直线
C.两条射线组成的图形叫做角
D.小于平角的角可分为锐角和钝角两类
8.已知∠AOB=30°,∠BOC=45°,则∠AOC等于( )
A.15° B.75° C.15°或75° D.不能确定
9.下列说法中,正确的有( )个
①笔尖在纸上快速滑动写出一个又一个字,这说明点动成线;②要整齐地栽一行树,只要确定两端的树坑位置,就能确定这一行树坑所在的直线,这是运用数学知识两点确定一条直线;③把一个直角三角形以直角边为轴旋转一周得到的几何体是圆柱;④ 射线AB与射线BA是同一条射线;⑤两条射线组成的图形叫角
A.1个 B.2个 C.3个 D.4
10.如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=50°,则∠1的度数是
A.70° B.65°
C.60° D.50°
11.下列四个说法中,正确的有( )个
(1)-24=(-2)4;(2)-|-1|=-(-1)3 (3)若a+1与b-1互为相反数,则2a+2b=0;(4)若线段AB=BC,则点B是线段AC的中点。
A.1 B.2 C.3 D.4
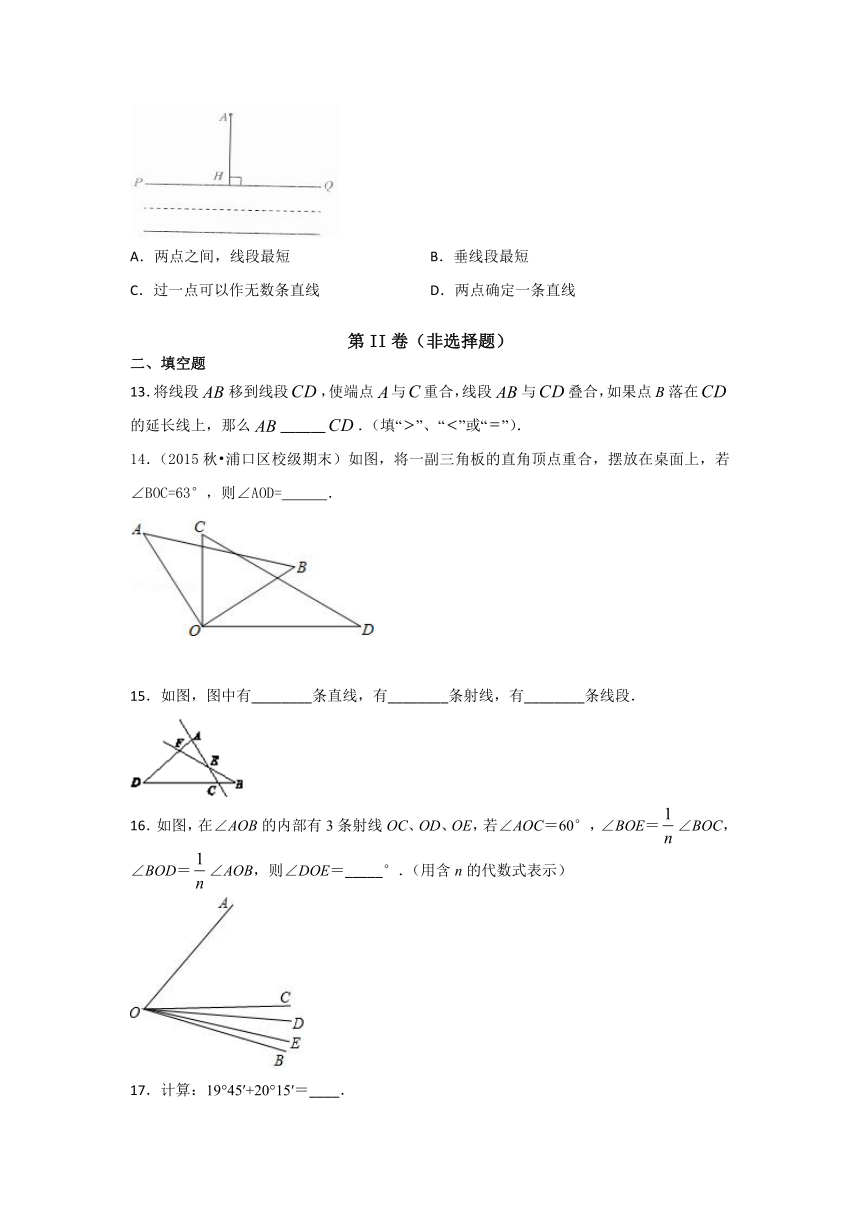
12.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是( )
A.两点之间,线段最短 B.垂线段最短
C.过一点可以作无数条直线 D.两点确定一条直线
第II卷(非选择题)
二、填空题
13.将线段移到线段,使端点与重合,线段与叠合,如果点落在的延长线上,那么______.(填“”、“”或“”).
14.(2015秋?浦口区校级期末)如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC=63°,则∠AOD= .
15.如图,图中有________条直线,有________条射线,有________条线段.
16.如图,在∠AOB的内部有3条射线OC、OD、OE,若∠AOC=60°,∠BOE=∠BOC,∠BOD=∠AOB,则∠DOE=_____°.(用含n的代数式表示)
17.计算:19°45′+20°15′=____.
18.82°32′5″+_____=180°.
19.若一个角的补角的余角是,则这个角的度数为__________.
20.如图,已知直线和相交于点,是直角,平分,,则的大小为__________.
三、解答题
21.如图,O为直线AB上一点,∠BOC=36°.
(1)若OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数:
(2)若∠AOD=∠AOC,∠DOE=60°,如图(b)所示,求∠AOE的度数:
(3)若∠AOD=∠AOC,∠DOE=(n≥2,且n为正整数),如图(c)所示,请用n含的代数式表示∠AOE的度数__________(直接写出结果).?
22.如图,已知线段AB=10cm,点C、D是线段AB上两点,且AC=BD=8cm,M、N分别是线段AC、AD的中点,求线段MN的长度.
23.电子跳蚤游戏盘为.,,,如果电子跳蚤开始时在边上点,.第一步跳蚤跳到边上点,且;第二步跳蚤从跳到边上点,且;第三步跳蚤从跳到边上点,且……跳蚤按上述规则跳下去,第次落到,请计算与之间的距离.
24.如图, 是直线上的一点,是直角,平分.若.求的度数.
25.如图,以直线 AB 上一点 O 为端点作射线 OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点 O 处.(注:∠DOE=90°)
(1)如图①,若直角三角板 DOE 的一边 OD 放在射线 OB 上,则∠COE= °;
(2)如图②,将直角三角板 DOE 绕点 O 逆时针方向转动到某个位置,若 OC 恰好平分∠BOE,求∠COD 的度数;
(3)如图③,将直角三角板 DOE 绕点 O 转动,如果 OD 始终在∠BOC 的内部, 试猜想∠BOD 和∠COE 有怎样的数量关系?并说明理由.
26.如图,线段AC=7cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使CN:NB=2:3,求MC,MN的长.
27.如图,四边形ABCD是正方形,对角线AC、BD相交于点O.求证:点A、B、C、D在以O为圆心的圆上.
28.已知线段AB=5cm,回答下列问题:是否存在一点C,使它到A、B两点的距离之和等于4?
29.已知:如图1,点M是线段AB上一定点,AB=12cm,C、D两点分别从M、B出发以1cm/s、2cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)
(1)若AM=4cm,当点C、D运动了2s,此时AC= ,DM= ;(直接填空)
(2)当点C、D运动了2s,求AC+MD的值.
(3)若点C、D运动时,总有MD=2AC,则AM= (填空)
(4)在(3)的条件下,N是直线AB上一点,且AN﹣BN=MN,求的值
参考答案
1.D2.C3.C4.D5.D6.B7.A8.C9.B10.B11.A12.B
13.
14.117°
15.1 9 12
16..
17.40°.
18.97°27′55″
19.118.
20.
21.(1)18°;(2)12°;(3).
22.3cm.
23.a
24.
25.(1)20;(2)20 ?;(3)∠COE﹣∠BOD=20°.
26.(1)CM=3.5cm;(2)MN=9.5m
28.不存在
29.(1)2,4;(2)6 cm;(3)4;(4)或1.
一、单选题
1.下面四个图形中,是多边形的是( )
A. B. C. D.
2.多边形的一个顶点处的所有对角线把多边形分成了11个三角形,则经过这一点的对角线的条数是(?? )
A.8 B.9 C.10 D.11
3.已知线段AB=8cm,在直线AB上画BC,使BC=2cm,则线段AC的长度是( )
A.6cm B.10cm C.6cm或10cm D.4cm或16cm
4.已知在同一平面内但不在同一条直线上的三点、、,画直线,画射线,连接.按照上述语句,画图正确的是( )
A.B. C. D.
5.植树时,为了使同一行树坑在一条直线上,只需定出两个树坑的位置,其中的数学道理是( )
A.两点之间线段最短
B.两点之间直线最短
C.两点确定一条射线
D.两点确定一条直线
6.如图,由A测B,方向是:
A.南偏东32 B.南偏东58 C.北偏西32 D.北偏西58
7.下列说法中正确的是( )
A.两点之间的所有连线中,线段最短
B.射线就是直线
C.两条射线组成的图形叫做角
D.小于平角的角可分为锐角和钝角两类
8.已知∠AOB=30°,∠BOC=45°,则∠AOC等于( )
A.15° B.75° C.15°或75° D.不能确定
9.下列说法中,正确的有( )个
①笔尖在纸上快速滑动写出一个又一个字,这说明点动成线;②要整齐地栽一行树,只要确定两端的树坑位置,就能确定这一行树坑所在的直线,这是运用数学知识两点确定一条直线;③把一个直角三角形以直角边为轴旋转一周得到的几何体是圆柱;④ 射线AB与射线BA是同一条射线;⑤两条射线组成的图形叫角
A.1个 B.2个 C.3个 D.4
10.如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=50°,则∠1的度数是
A.70° B.65°
C.60° D.50°
11.下列四个说法中,正确的有( )个
(1)-24=(-2)4;(2)-|-1|=-(-1)3 (3)若a+1与b-1互为相反数,则2a+2b=0;(4)若线段AB=BC,则点B是线段AC的中点。
A.1 B.2 C.3 D.4
12.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是( )
A.两点之间,线段最短 B.垂线段最短
C.过一点可以作无数条直线 D.两点确定一条直线
第II卷(非选择题)
二、填空题
13.将线段移到线段,使端点与重合,线段与叠合,如果点落在的延长线上,那么______.(填“”、“”或“”).
14.(2015秋?浦口区校级期末)如图,将一副三角板的直角顶点重合,摆放在桌面上,若∠BOC=63°,则∠AOD= .
15.如图,图中有________条直线,有________条射线,有________条线段.
16.如图,在∠AOB的内部有3条射线OC、OD、OE,若∠AOC=60°,∠BOE=∠BOC,∠BOD=∠AOB,则∠DOE=_____°.(用含n的代数式表示)
17.计算:19°45′+20°15′=____.
18.82°32′5″+_____=180°.
19.若一个角的补角的余角是,则这个角的度数为__________.
20.如图,已知直线和相交于点,是直角,平分,,则的大小为__________.
三、解答题
21.如图,O为直线AB上一点,∠BOC=36°.
(1)若OD平分∠AOC,∠DOE=90°,如图(a)所示,求∠AOE的度数:
(2)若∠AOD=∠AOC,∠DOE=60°,如图(b)所示,求∠AOE的度数:
(3)若∠AOD=∠AOC,∠DOE=(n≥2,且n为正整数),如图(c)所示,请用n含的代数式表示∠AOE的度数__________(直接写出结果).?
22.如图,已知线段AB=10cm,点C、D是线段AB上两点,且AC=BD=8cm,M、N分别是线段AC、AD的中点,求线段MN的长度.
23.电子跳蚤游戏盘为.,,,如果电子跳蚤开始时在边上点,.第一步跳蚤跳到边上点,且;第二步跳蚤从跳到边上点,且;第三步跳蚤从跳到边上点,且……跳蚤按上述规则跳下去,第次落到,请计算与之间的距离.
24.如图, 是直线上的一点,是直角,平分.若.求的度数.
25.如图,以直线 AB 上一点 O 为端点作射线 OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点 O 处.(注:∠DOE=90°)
(1)如图①,若直角三角板 DOE 的一边 OD 放在射线 OB 上,则∠COE= °;
(2)如图②,将直角三角板 DOE 绕点 O 逆时针方向转动到某个位置,若 OC 恰好平分∠BOE,求∠COD 的度数;
(3)如图③,将直角三角板 DOE 绕点 O 转动,如果 OD 始终在∠BOC 的内部, 试猜想∠BOD 和∠COE 有怎样的数量关系?并说明理由.
26.如图,线段AC=7cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使CN:NB=2:3,求MC,MN的长.
27.如图,四边形ABCD是正方形,对角线AC、BD相交于点O.求证:点A、B、C、D在以O为圆心的圆上.
28.已知线段AB=5cm,回答下列问题:是否存在一点C,使它到A、B两点的距离之和等于4?
29.已知:如图1,点M是线段AB上一定点,AB=12cm,C、D两点分别从M、B出发以1cm/s、2cm/s的速度沿直线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)
(1)若AM=4cm,当点C、D运动了2s,此时AC= ,DM= ;(直接填空)
(2)当点C、D运动了2s,求AC+MD的值.
(3)若点C、D运动时,总有MD=2AC,则AM= (填空)
(4)在(3)的条件下,N是直线AB上一点,且AN﹣BN=MN,求的值
参考答案
1.D2.C3.C4.D5.D6.B7.A8.C9.B10.B11.A12.B
13.
14.117°
15.1 9 12
16..
17.40°.
18.97°27′55″
19.118.
20.
21.(1)18°;(2)12°;(3).
22.3cm.
23.a
24.
25.(1)20;(2)20 ?;(3)∠COE﹣∠BOD=20°.
26.(1)CM=3.5cm;(2)MN=9.5m
28.不存在
29.(1)2,4;(2)6 cm;(3)4;(4)或1.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
