1.5 加速度 粤教版—【新教材】粤教版(2019)高一物理必修一 课件(共28张PPT)
文档属性
| 名称 | 1.5 加速度 粤教版—【新教材】粤教版(2019)高一物理必修一 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
1.5
加速度
第一章
运动的描述
法拉利F2003
-GA赛车,
369km/h
“飓风2000”战斗机,
2450km/h
舒马赫
1、赛车为什么能在第1项短距离(600米)
的比赛中先拔头筹?
思考
2、仅仅用位移和速度
能否满足我们描述物
体运动的需求?
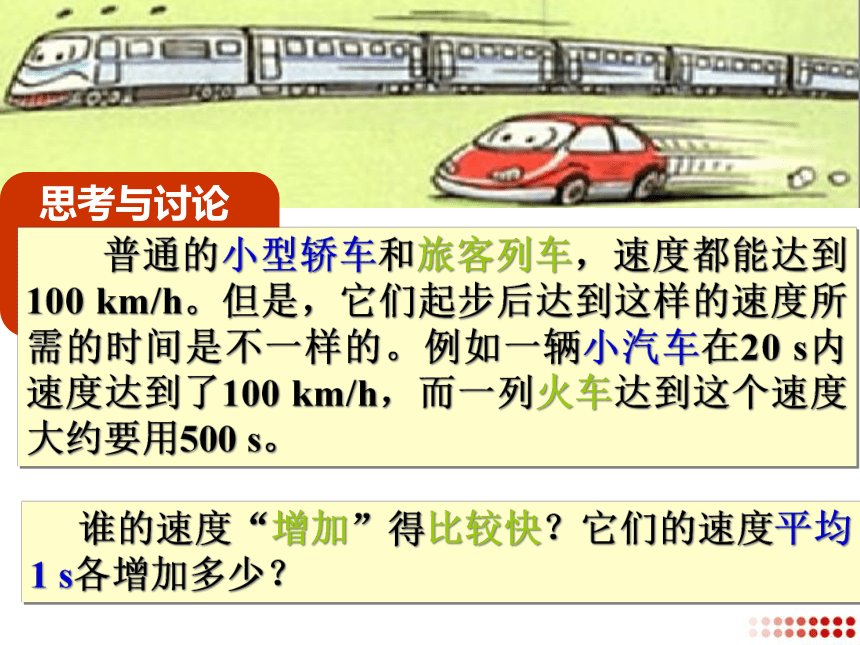
思考与讨论
普通的小型轿车和旅客列车,速度都能达到100
km/h。但是,它们起步后达到这样的速度所需的时间是不一样的。例如一辆小汽车在20
s内速度达到了100
km/h,而一列火车达到这个速度大约要用500
s。
谁的速度“增加”得比较快?它们的速度平均1
s各增加多少?
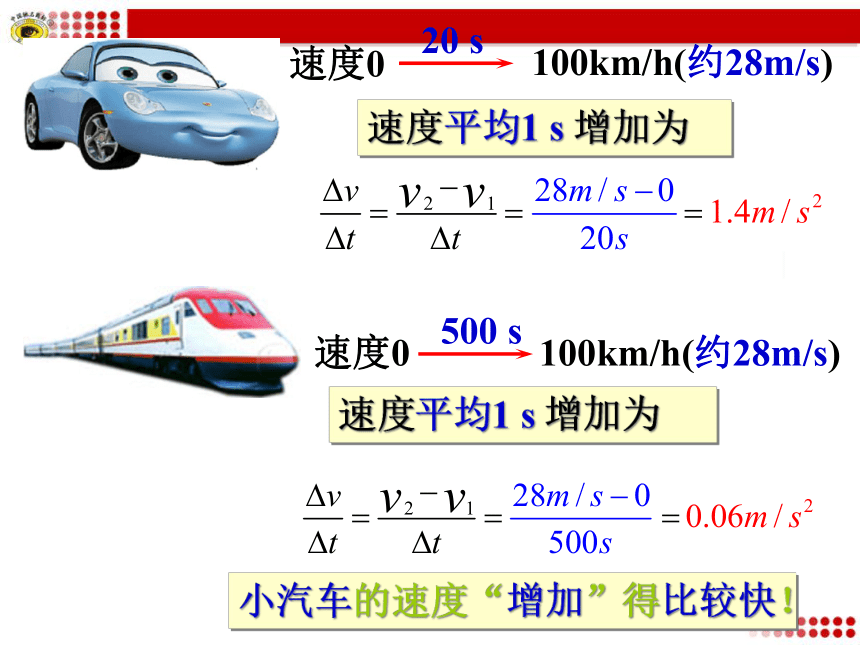
小汽车的速度“增加”得比较快!
20
s
速度0
100km/h(约28m/s)
速度平均1
s
增加为
500
s
速度0
100km/h(约28m/s)
速度平均1
s
增加为
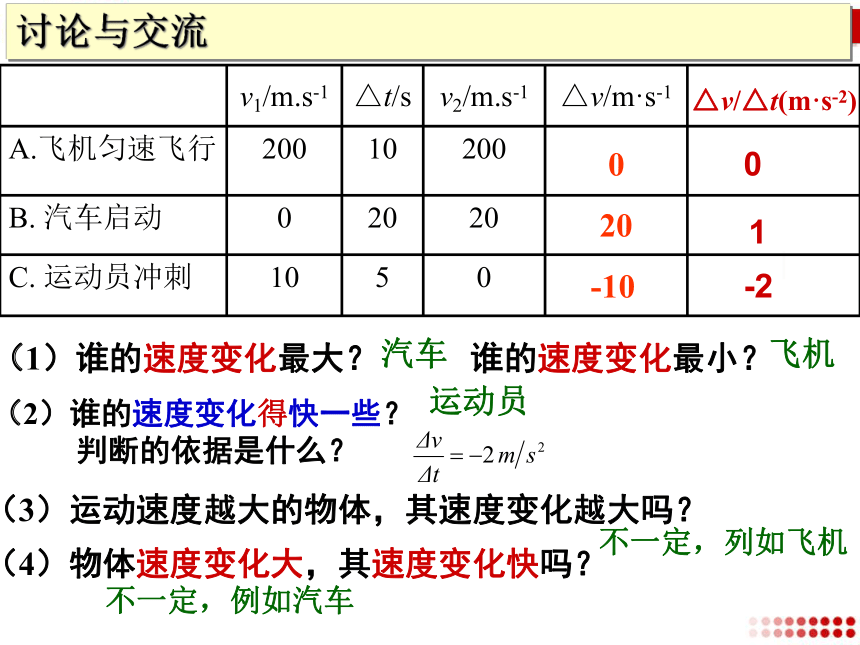
v1/m.s-1
△t/s
v2/m.s-1
△v/m·s-1
A.飞机匀速飞行
200
10
200
B.
汽车启动
0
20
20
C.
运动员冲刺
10
5
0
0
-10
20
(1)谁的速度变化最大?
谁的速度变化最小?
(2)谁的速度变化得快一些?
判断的依据是什么?
讨论与交流
(4)物体速度变化大,其速度变化快吗?
△v/△t(m·s-2)
0
1
-2
(3)运动速度越大的物体,其速度变化越大吗?
汽车
飞机
运动员
不一定,列如飞机
不一定,例如汽车
加速度
⒈
定义:
v0----初速度
vt----末速度
⒉
定义式:
a
----加速度
⒊单位:m/s2
(读:米每二次方秒或米每平方秒)
5、物理意义:描述物体速度变化的“快慢”
速度的变化量跟发生这一变化所用时间的比值。
符号
a
4、矢量性:大小:等于单位时间内速度的变化量。
方向:与速度变化量△v的方向相同
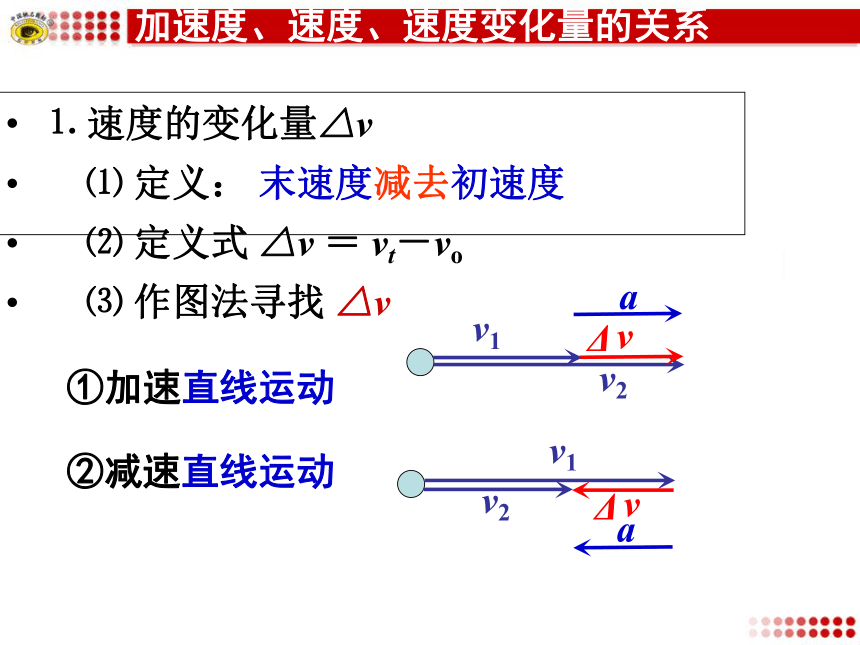
加速度、速度、速度变化量的关系
⒈
速度的变化量△v
⑴
定义:
末速度减去初速度
⑵
定义式
△v
=
vt-vo
⑶
作图法寻找
△v
Δ
v
v1
v2
Δ
v
v1
v2
①加速直线运动
②减速直线运动
a
a
⒉
加速度
(a
=
△v/△t
)的方向
在变速直线运动中,若以初速度v0方向为正方向,
①
加速直线运动,a
___0,a的方向
;
②
减速直线运动,a
___0,
a的方向
。
结论:加速度方向和速度变化量的方向相同,与速度方向无关。
>
与v0方向相同
<
与v0方向相反
例题:某高层建筑物内有一台正在向上运行的电梯,乘客按下楼层键后,电梯的速度在1.5s内由2.4m/s均匀减小到零。求该电梯的加速度。
解:取竖直向上(初速度方向)为正方向。
电梯的加速度大小为
,方向竖直向下。
【注意】
1、在运算中必须规定正方向,通常以初速方向为正方向。则与正方向同向的物理量取为正,与正方向相反的物理量取为负。
2、速度变化量Δv=v-v0的运算一定是末速v
减去初速v0。
3、要注意分析加速度的方向及计算结果中的正、负符号的物理意义。
图像中的加速度表示
E
F
b1
根据加速度的定义式:
加速度等于直线b1的斜率
b2
直线b1比b2更陡些,直线b1的斜率比直线b2的斜率更大,所以直线b1所对应物体的加速度大。
思考
“速度大”、“速度变化大”、“速度变化得快”描述的意思相同吗?
三者之间没有必然联系!
1)速度大,加速度也一定大吗?
2)速度变化量大,加速度也一定大吗?
不一定,例如:匀速直线运动
【思考与讨论】
3)速度变化快的物体,加速度一定大吗?
一
定
还与所用时间有关
5)物体的速度为零时,加速度一定为零吗?
不一定,
竖直上抛运动到达最高点
速度为零,加速度不为零,加速度等
于重力加速度
4)加速度为零时,速度也一定为零吗?
不一定,例如:匀速直线运动
a与V0关系
总之,只要a与V0方向相同,不论a是变大还是变小或是不变,V一定增大;
若a与V0方向相同,
表示是加速运动
当a不变时,表示物体速度______增加
当a增大时,表示物体速度减小得越来越____
当a不变时,表示物体速度_______减小
若a与V0方向相反,
表示是减速运动
当a减小时,表示物体速度减小得越来越____
总之,只要a与V0方向相反,不论a是变大还是变小或是不变,V一定减小;
当a增大时,表示物体速度增加得越来越____
当a减小时,表示物体速度增加得越来越____
快
慢
均匀
慢
快
均匀
速度与加速度的比较
定义
物理意义
速度
平均速度
瞬时速度
加速度
平均加速度
瞬时加速度
在匀速直线运动中瞬时速度保持不变,且平均速度与瞬时速度相等
瞬时加速度保持不变的直线运动称为匀变速直线运动,在该运动中,平均加速度与瞬时加速度相等。
描述一段时间或一段位移内物体运动的快慢
描述某一时刻或某一位置物体运动的快慢
描述一段时间或一段位移内速度变化的快慢
描述某一时刻或某一位置速度变化的快慢
如果物体沿直线运动且其速度均匀变化(增加或减少),该物体的运动就是匀变速直线运动,此时加速度不随时间改变。(加速度大小、方向都不变)
加速度越大,物体的速度改变得越快
匀变速直线运动
匀加速直线运动
匀减速直线运动
D
⒈
下列说法正确的是
(
)
A.
物体速度改变量大,其加速度一定大
B.
物体有加速度时,速度就增大
C.
物体的加速度大,速度一定大
D.
物体的速度变化快,加速度一定大
课堂练习
⒉
关于加速度的含义,下列说法正确的是:( )
A.
加速度表示速度的增加
B.
加速度表示速度变化
C.
加速度表示速度变化快慢
D.
加速度表示速度变化的大小
C
⒊
下列说法正确的是:( )
A.
加速度增大,速度一定增大
B.
速度变化越大,加速度越大
C.
物体有加速度,速度就增大
D.
物体的速度很大,加速度可能为零
D
4.
关于速度、速度改变量、加速度,正确的说法是:( )
A、物体运动的速度改变量很大,它的加速度一定很大
B、速度很大的物体,其加速度可以很小,可以为零
C、某时刻物体的速度为零,其加速度不可能为零
D、加速度很大时,运动物体的速度一定很大
B
考:
5.
某物体做匀加速直线运动,已知加速度为2
m/s2
那么在任意1s
内(
)
A、物体的末速度一定等于初速度的两倍
B、物体的末速度一定比初速度大2
m/s
C、物体的末速度一定比前1s内的末速度
大2
m/s
D、物体的末速度一定比前1s内的初速度
大2m/s
BC
6、
足球以8m/s的速度飞来,运动员以12m/s的速率反向踢回,踢球时间为0.2s,设球飞来方向为正方向,则足球在这段时间内的加速度为多少?
解:设球飞来的方向为正方向
方向与足球原来运动方向相反
所需时间
课本例题:某高层建筑物内一部正在向上运行的电梯,在1.5s内速度由2.4m/s均匀减少到0,求电梯的加速度?
解:电梯的运动是匀变速直线运动,选取竖直向上为正方向,根据加速度的定义可得
电梯的加速度大小为1.6m/s2,方向竖直向下
课后思考题:1、加速度(a)
例如,一辆摩托车以36km/h行驶,突然与一硬墙发生碰撞,碰撞时间1毫秒(即摩托车车速减至零所经时间),试判断该摩托车车手有生命危险吗?请说明理由。
死亡加速度:西方交通管理部门为了交通安全,特制定了死亡加速度5000m/s2这一数值,以醒世人。意思是如果行车加速度超过此值,将有生命危险。
计算下列过程的加速度:
(1)一辆汽车从车站出发做直线运动,经10
s速度达到108
km/h;
【解析】 规定以初速度方向为正方向,则
(1)汽车初速度为v0=0,
汽车末速度为vt=108
km/h=30
m/s,
所需时间t=10
s.由加速度定义得:
方向与初速度方向相同.
(2)在高速公路上汽车做直线运动,经3
min速度从54
km/h提高到144
km/h;
(2)汽车初速度为
方向与初速度方向相同.
汽车末速度为
所需时间
由加速度定义得
1.5
加速度
第一章
运动的描述
法拉利F2003
-GA赛车,
369km/h
“飓风2000”战斗机,
2450km/h
舒马赫
1、赛车为什么能在第1项短距离(600米)
的比赛中先拔头筹?
思考
2、仅仅用位移和速度
能否满足我们描述物
体运动的需求?
思考与讨论
普通的小型轿车和旅客列车,速度都能达到100
km/h。但是,它们起步后达到这样的速度所需的时间是不一样的。例如一辆小汽车在20
s内速度达到了100
km/h,而一列火车达到这个速度大约要用500
s。
谁的速度“增加”得比较快?它们的速度平均1
s各增加多少?
小汽车的速度“增加”得比较快!
20
s
速度0
100km/h(约28m/s)
速度平均1
s
增加为
500
s
速度0
100km/h(约28m/s)
速度平均1
s
增加为
v1/m.s-1
△t/s
v2/m.s-1
△v/m·s-1
A.飞机匀速飞行
200
10
200
B.
汽车启动
0
20
20
C.
运动员冲刺
10
5
0
0
-10
20
(1)谁的速度变化最大?
谁的速度变化最小?
(2)谁的速度变化得快一些?
判断的依据是什么?
讨论与交流
(4)物体速度变化大,其速度变化快吗?
△v/△t(m·s-2)
0
1
-2
(3)运动速度越大的物体,其速度变化越大吗?
汽车
飞机
运动员
不一定,列如飞机
不一定,例如汽车
加速度
⒈
定义:
v0----初速度
vt----末速度
⒉
定义式:
a
----加速度
⒊单位:m/s2
(读:米每二次方秒或米每平方秒)
5、物理意义:描述物体速度变化的“快慢”
速度的变化量跟发生这一变化所用时间的比值。
符号
a
4、矢量性:大小:等于单位时间内速度的变化量。
方向:与速度变化量△v的方向相同
加速度、速度、速度变化量的关系
⒈
速度的变化量△v
⑴
定义:
末速度减去初速度
⑵
定义式
△v
=
vt-vo
⑶
作图法寻找
△v
Δ
v
v1
v2
Δ
v
v1
v2
①加速直线运动
②减速直线运动
a
a
⒉
加速度
(a
=
△v/△t
)的方向
在变速直线运动中,若以初速度v0方向为正方向,
①
加速直线运动,a
___0,a的方向
;
②
减速直线运动,a
___0,
a的方向
。
结论:加速度方向和速度变化量的方向相同,与速度方向无关。
>
与v0方向相同
<
与v0方向相反
例题:某高层建筑物内有一台正在向上运行的电梯,乘客按下楼层键后,电梯的速度在1.5s内由2.4m/s均匀减小到零。求该电梯的加速度。
解:取竖直向上(初速度方向)为正方向。
电梯的加速度大小为
,方向竖直向下。
【注意】
1、在运算中必须规定正方向,通常以初速方向为正方向。则与正方向同向的物理量取为正,与正方向相反的物理量取为负。
2、速度变化量Δv=v-v0的运算一定是末速v
减去初速v0。
3、要注意分析加速度的方向及计算结果中的正、负符号的物理意义。
图像中的加速度表示
E
F
b1
根据加速度的定义式:
加速度等于直线b1的斜率
b2
直线b1比b2更陡些,直线b1的斜率比直线b2的斜率更大,所以直线b1所对应物体的加速度大。
思考
“速度大”、“速度变化大”、“速度变化得快”描述的意思相同吗?
三者之间没有必然联系!
1)速度大,加速度也一定大吗?
2)速度变化量大,加速度也一定大吗?
不一定,例如:匀速直线运动
【思考与讨论】
3)速度变化快的物体,加速度一定大吗?
一
定
还与所用时间有关
5)物体的速度为零时,加速度一定为零吗?
不一定,
竖直上抛运动到达最高点
速度为零,加速度不为零,加速度等
于重力加速度
4)加速度为零时,速度也一定为零吗?
不一定,例如:匀速直线运动
a与V0关系
总之,只要a与V0方向相同,不论a是变大还是变小或是不变,V一定增大;
若a与V0方向相同,
表示是加速运动
当a不变时,表示物体速度______增加
当a增大时,表示物体速度减小得越来越____
当a不变时,表示物体速度_______减小
若a与V0方向相反,
表示是减速运动
当a减小时,表示物体速度减小得越来越____
总之,只要a与V0方向相反,不论a是变大还是变小或是不变,V一定减小;
当a增大时,表示物体速度增加得越来越____
当a减小时,表示物体速度增加得越来越____
快
慢
均匀
慢
快
均匀
速度与加速度的比较
定义
物理意义
速度
平均速度
瞬时速度
加速度
平均加速度
瞬时加速度
在匀速直线运动中瞬时速度保持不变,且平均速度与瞬时速度相等
瞬时加速度保持不变的直线运动称为匀变速直线运动,在该运动中,平均加速度与瞬时加速度相等。
描述一段时间或一段位移内物体运动的快慢
描述某一时刻或某一位置物体运动的快慢
描述一段时间或一段位移内速度变化的快慢
描述某一时刻或某一位置速度变化的快慢
如果物体沿直线运动且其速度均匀变化(增加或减少),该物体的运动就是匀变速直线运动,此时加速度不随时间改变。(加速度大小、方向都不变)
加速度越大,物体的速度改变得越快
匀变速直线运动
匀加速直线运动
匀减速直线运动
D
⒈
下列说法正确的是
(
)
A.
物体速度改变量大,其加速度一定大
B.
物体有加速度时,速度就增大
C.
物体的加速度大,速度一定大
D.
物体的速度变化快,加速度一定大
课堂练习
⒉
关于加速度的含义,下列说法正确的是:( )
A.
加速度表示速度的增加
B.
加速度表示速度变化
C.
加速度表示速度变化快慢
D.
加速度表示速度变化的大小
C
⒊
下列说法正确的是:( )
A.
加速度增大,速度一定增大
B.
速度变化越大,加速度越大
C.
物体有加速度,速度就增大
D.
物体的速度很大,加速度可能为零
D
4.
关于速度、速度改变量、加速度,正确的说法是:( )
A、物体运动的速度改变量很大,它的加速度一定很大
B、速度很大的物体,其加速度可以很小,可以为零
C、某时刻物体的速度为零,其加速度不可能为零
D、加速度很大时,运动物体的速度一定很大
B
考:
5.
某物体做匀加速直线运动,已知加速度为2
m/s2
那么在任意1s
内(
)
A、物体的末速度一定等于初速度的两倍
B、物体的末速度一定比初速度大2
m/s
C、物体的末速度一定比前1s内的末速度
大2
m/s
D、物体的末速度一定比前1s内的初速度
大2m/s
BC
6、
足球以8m/s的速度飞来,运动员以12m/s的速率反向踢回,踢球时间为0.2s,设球飞来方向为正方向,则足球在这段时间内的加速度为多少?
解:设球飞来的方向为正方向
方向与足球原来运动方向相反
所需时间
课本例题:某高层建筑物内一部正在向上运行的电梯,在1.5s内速度由2.4m/s均匀减少到0,求电梯的加速度?
解:电梯的运动是匀变速直线运动,选取竖直向上为正方向,根据加速度的定义可得
电梯的加速度大小为1.6m/s2,方向竖直向下
课后思考题:1、加速度(a)
例如,一辆摩托车以36km/h行驶,突然与一硬墙发生碰撞,碰撞时间1毫秒(即摩托车车速减至零所经时间),试判断该摩托车车手有生命危险吗?请说明理由。
死亡加速度:西方交通管理部门为了交通安全,特制定了死亡加速度5000m/s2这一数值,以醒世人。意思是如果行车加速度超过此值,将有生命危险。
计算下列过程的加速度:
(1)一辆汽车从车站出发做直线运动,经10
s速度达到108
km/h;
【解析】 规定以初速度方向为正方向,则
(1)汽车初速度为v0=0,
汽车末速度为vt=108
km/h=30
m/s,
所需时间t=10
s.由加速度定义得:
方向与初速度方向相同.
(2)在高速公路上汽车做直线运动,经3
min速度从54
km/h提高到144
km/h;
(2)汽车初速度为
方向与初速度方向相同.
汽车末速度为
所需时间
由加速度定义得
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
