五年级【数学(北京版)】平均数(第二课时)-课件(39张PPT)
文档属性
| 名称 | 五年级【数学(北京版)】平均数(第二课时)-课件(39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 39.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览









文档简介
平均数(第二课时)
五年级 数学
学习准备
计算器
我会计算比较复杂数据的平均数了。
平均数可以刻画一组数据的整体水平。
哪里还会用到平均数呢?
还可以怎样分析数据呢?
阳光小学五年级举办男子立定跳远比赛,每个班推荐1名队员参赛。五(1)班的王阳和陆强报名参赛。应该推荐谁去呢?
任务一:解决问题
任务一:解决问题
可以让两位同学到操场上比一比,看看谁跳的远,跳得远的同学去。
只跳一次还不行,可以多跳几次,看看谁的成绩整体比较好。
体育课上老师会给我们测试跳远,可以找到体育老师,把之前两位同学的成绩找出来比较一下。
{5940675A-B579-460E-94D1-54222C63F5DA}
测试1
测试2
测试3
测试4
测试5
测试6
王阳
1.97
2.04
2.10
1.99
1.70
2.01
陆强
1.76
2.04
1.82
2.13
2.10
1.65
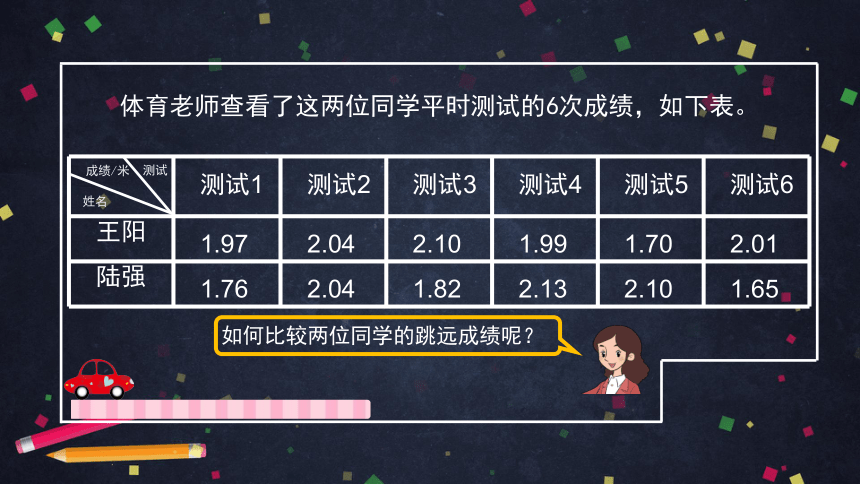
体育老师查看了这两位同学平时测试的6次成绩,如下表。
如何比较两位同学的跳远成绩呢?
测试
成绩/米
姓名
王阳:1.70 1.97 1.99 2.01 2.04 2.10
陆强:1.65 1.76 1.82 2.04 2.10 2.13
将两个人6次测试成绩从低到高排序,逐一比较。
王阳:1.70 1.97 1.99 2.01 2.04 2.10
陆强:1.65 1.76 1.82 2.04 2.10 2.13
比较两个人的最好成绩。
陆强的最好成绩高于王阳。
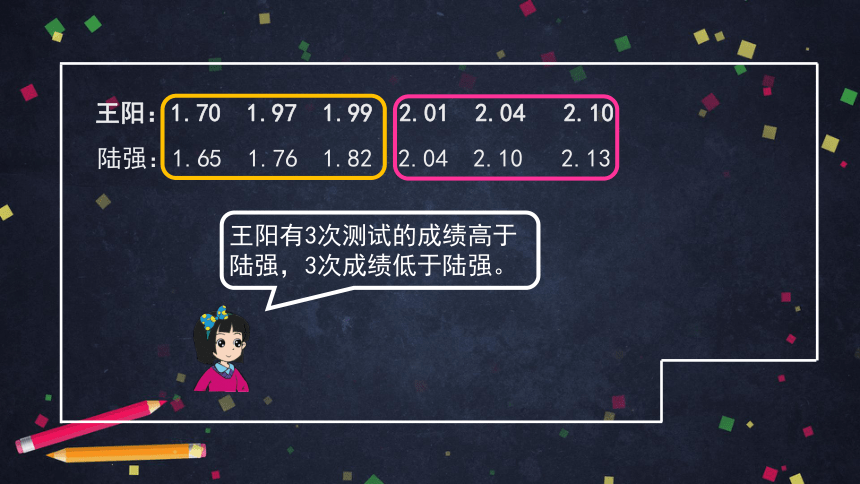
王阳:1.70 1.97 1.99 2.01 2.04 2.10
陆强:1.65 1.76 1.82 2.04 2.10 2.13
王阳有3次测试的成绩高于陆强,3次成绩低于陆强。
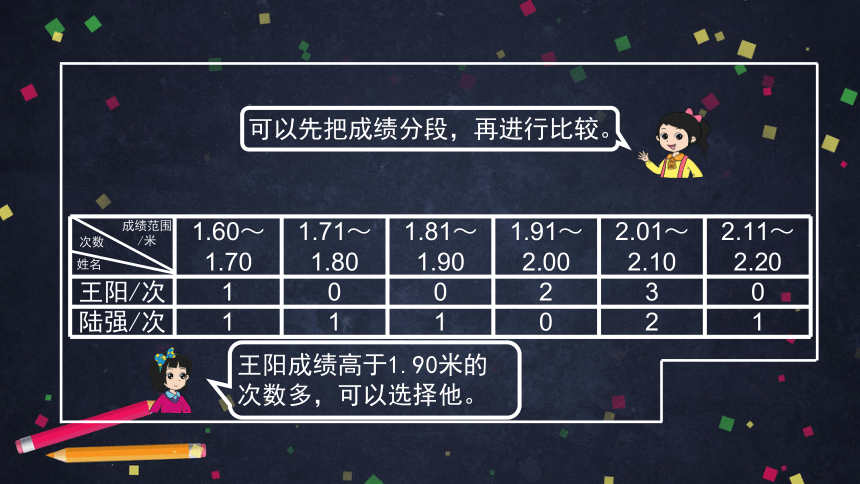
可以先把成绩分段,再进行比较。
{5940675A-B579-460E-94D1-54222C63F5DA}
1.60~1.70
1.71~1.80
1.81~1.90
1.91~2.00
2.01~2.10
2.11~2.20
王阳/次
1
0
0
2
3
0
陆强/次
1
1
1
0
2
1
成绩范围
/米
次数
姓名
王阳成绩高于1.90米的次数多,可以选择他。
可以比较两位同学6次测试的平均成绩。
王阳:1.70 1.97 1.99 2.01 2.04 2.10
陆强:1.65 1.76 1.82 2.04 2.10 2.13
王阳:
(1.70+1.97+1.99+2.01+2.04+2.10)÷6≈1.97(米)
陆强:
(1.65+1.76+1.82+2.04+2.10+2.13)÷6≈ 1.92(米)
1.97米>1.92米
王阳的整体水平略高于陆强的整体水平。
到底该推荐谁参赛呢?
我觉得可以派陆强参赛,
他的最好成绩高于王阳。
可以派王阳参赛,他的平均成绩高于陆强。
遇到问题要先收集数据,通过
分析数据,做出合理的判断。
对于同一组数据,可以有不同
的分析方法。要根据具体的情
况选择合适的方法分析数据。
平均数能刻画一组数据的整体水平。
西郊小学五年级要举办书香班级的评比,现在需要了解每个班现有的小图书馆的存书数量,每个班的存书数量如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}班级
人数
存书/本
五(1)班
30
360
五(2)班
28
420
五(3)班
32
576
五(4)班
30
480
如何比较4个班的存书情况?
可以比较4个班存书的总本数。
360<420<480<576
五(1)班的存书数量最少,
五(3)班的存书数量最多。
比较4个班平均每个同学存书的本数。
360÷30=12(本)
420÷28=15(本)
576÷32=18(本)
480÷30=16(本)
12<15<16<18
五(1)班人均存书最少,五(3)班人均存书最多。
比较4个班人均存书数量和整个年级人均存书
数量。需要先求出全年级人均存书数量:
(12+15+18+16)÷4=61÷4=15.25(本)
(360+420+576+480)÷(30+28+32+30)
=1836÷120
=15.30(本)
第二种方法正确。要求的是全年级的人均存书数量,要用全年级的总数量除以全年级的总人数,得到的才是全年级的人均存书数量,也就是要把所有的存书在全年级内匀一匀,让每个人的数量都相等。
哪种计算方法正确呢?
比较班级人均存书本数和年级人均存书本数,你有什么发现?
{5940675A-B579-460E-94D1-54222C63F5DA}班级
人数
存书/本
人均存书/本
合计
120
1836
15.30
五(1)班
30
360
12
五(2)班
28
420
15
五(3)班
32
576
18
五(4)班
30
480
16
年级人均存书数量在五(1)班人均存书
数量和五(3)班人均存书数量之间。
五(1)班、五(2)班的人均存书数
量低于年级人均存书数量,五(3)
班、五(4)班的人均存书数量高
于年级人均存书数量。
任务二:巩固应用
平均数有着广泛的应用。
日平均气温的变化标志着季节的变化。在气象学中,可以用日平均气温计算入春日、入夏日、入秋日、入冬日。入秋日:连续5日的日平均气温低于22℃,第一天即为入秋日。
如何计算日平均气温呢?
资料
{2D5ABB26-0587-4C30-8999-92F81FD0307C}2时
4时
6时
8时
10时
12时
14时
16时
18时
20时
22时
24时
16
14
14
18
22
24
26
26
22
18
17
16
下面是北京市入秋以来某日的气温情况。(单位:℃)
请你计算北京市这一天的日平均气温。
{2D5ABB26-0587-4C30-8999-92F81FD0307C}2时
4时
6时
8时
10时
12时
14时
16时
18时
20时
22时
24时
16
14
14
18
22
24
26
26
22
18
17
16
下面是北京市入秋以来某日的气温情况。(单位:℃)
(16+18+26+18)÷4
=78÷4
=19.5( ℃ )
答:北京市这一天的日平均气温为19.5 ℃。
{2D5ABB26-0587-4C30-8999-92F81FD0307C}2时
4时
6时
8时
10时
12时
14时
16时
18时
20时
22时
24时
16
14
14
18
22
24
26
26
22
18
17
16
生活中,哪里还有平均数?
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
(1)计算每个班的平均分,排出名次。(结果保留一位小数)
评委
成绩/分
班级
四(1)班:
(92+97+99+97+95)÷5=96.0(分)
四(2)班:
(82+98+98+100+94)÷5=94.4(分)
四(3)班
(89+97+99+98+92)÷5=95.0(分)
96.0>95.0>94.4
四(1)班第1名,四(3)班第2名,四(2)班第3名。
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
(2)如果去掉一个最高分,去掉一个最低分,再计算平均分。(结果保留一位小数)
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
四(1)班:
(97+97+95)÷3≈96.3(分)
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
四(2)班:
(98+98+94)÷3≈96.7(分)
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
四(3)班
(97+98+92)÷3≈95.7(分)
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
96.7>96.3>95.7
四(2)班第1名,四(1)班第2名,
四(3)班第3名。
四(2)班有一个数据是82分,把平均分拉低了,每个数据都会影响平均分。
两种计算方法,得到的平均分不一样。
平均数在生活中有着广泛的应用。
你的问题得到解决了吗?
选择合适的方法分析数据,根据数据做出判断。
对于同一组数据可以有多种分析方法。
1.数学书第80页第4题。
课后作业
2.数学书第103页第9题。
课后作业
3.继续寻找生活中与平均数有关的实例。
再 见
五年级 数学
学习准备
计算器
我会计算比较复杂数据的平均数了。
平均数可以刻画一组数据的整体水平。
哪里还会用到平均数呢?
还可以怎样分析数据呢?
阳光小学五年级举办男子立定跳远比赛,每个班推荐1名队员参赛。五(1)班的王阳和陆强报名参赛。应该推荐谁去呢?
任务一:解决问题
任务一:解决问题
可以让两位同学到操场上比一比,看看谁跳的远,跳得远的同学去。
只跳一次还不行,可以多跳几次,看看谁的成绩整体比较好。
体育课上老师会给我们测试跳远,可以找到体育老师,把之前两位同学的成绩找出来比较一下。
{5940675A-B579-460E-94D1-54222C63F5DA}
测试1
测试2
测试3
测试4
测试5
测试6
王阳
1.97
2.04
2.10
1.99
1.70
2.01
陆强
1.76
2.04
1.82
2.13
2.10
1.65
体育老师查看了这两位同学平时测试的6次成绩,如下表。
如何比较两位同学的跳远成绩呢?
测试
成绩/米
姓名
王阳:1.70 1.97 1.99 2.01 2.04 2.10
陆强:1.65 1.76 1.82 2.04 2.10 2.13
将两个人6次测试成绩从低到高排序,逐一比较。
王阳:1.70 1.97 1.99 2.01 2.04 2.10
陆强:1.65 1.76 1.82 2.04 2.10 2.13
比较两个人的最好成绩。
陆强的最好成绩高于王阳。
王阳:1.70 1.97 1.99 2.01 2.04 2.10
陆强:1.65 1.76 1.82 2.04 2.10 2.13
王阳有3次测试的成绩高于陆强,3次成绩低于陆强。
可以先把成绩分段,再进行比较。
{5940675A-B579-460E-94D1-54222C63F5DA}
1.60~1.70
1.71~1.80
1.81~1.90
1.91~2.00
2.01~2.10
2.11~2.20
王阳/次
1
0
0
2
3
0
陆强/次
1
1
1
0
2
1
成绩范围
/米
次数
姓名
王阳成绩高于1.90米的次数多,可以选择他。
可以比较两位同学6次测试的平均成绩。
王阳:1.70 1.97 1.99 2.01 2.04 2.10
陆强:1.65 1.76 1.82 2.04 2.10 2.13
王阳:
(1.70+1.97+1.99+2.01+2.04+2.10)÷6≈1.97(米)
陆强:
(1.65+1.76+1.82+2.04+2.10+2.13)÷6≈ 1.92(米)
1.97米>1.92米
王阳的整体水平略高于陆强的整体水平。
到底该推荐谁参赛呢?
我觉得可以派陆强参赛,
他的最好成绩高于王阳。
可以派王阳参赛,他的平均成绩高于陆强。
遇到问题要先收集数据,通过
分析数据,做出合理的判断。
对于同一组数据,可以有不同
的分析方法。要根据具体的情
况选择合适的方法分析数据。
平均数能刻画一组数据的整体水平。
西郊小学五年级要举办书香班级的评比,现在需要了解每个班现有的小图书馆的存书数量,每个班的存书数量如下表:
{5940675A-B579-460E-94D1-54222C63F5DA}班级
人数
存书/本
五(1)班
30
360
五(2)班
28
420
五(3)班
32
576
五(4)班
30
480
如何比较4个班的存书情况?
可以比较4个班存书的总本数。
360<420<480<576
五(1)班的存书数量最少,
五(3)班的存书数量最多。
比较4个班平均每个同学存书的本数。
360÷30=12(本)
420÷28=15(本)
576÷32=18(本)
480÷30=16(本)
12<15<16<18
五(1)班人均存书最少,五(3)班人均存书最多。
比较4个班人均存书数量和整个年级人均存书
数量。需要先求出全年级人均存书数量:
(12+15+18+16)÷4=61÷4=15.25(本)
(360+420+576+480)÷(30+28+32+30)
=1836÷120
=15.30(本)
第二种方法正确。要求的是全年级的人均存书数量,要用全年级的总数量除以全年级的总人数,得到的才是全年级的人均存书数量,也就是要把所有的存书在全年级内匀一匀,让每个人的数量都相等。
哪种计算方法正确呢?
比较班级人均存书本数和年级人均存书本数,你有什么发现?
{5940675A-B579-460E-94D1-54222C63F5DA}班级
人数
存书/本
人均存书/本
合计
120
1836
15.30
五(1)班
30
360
12
五(2)班
28
420
15
五(3)班
32
576
18
五(4)班
30
480
16
年级人均存书数量在五(1)班人均存书
数量和五(3)班人均存书数量之间。
五(1)班、五(2)班的人均存书数
量低于年级人均存书数量,五(3)
班、五(4)班的人均存书数量高
于年级人均存书数量。
任务二:巩固应用
平均数有着广泛的应用。
日平均气温的变化标志着季节的变化。在气象学中,可以用日平均气温计算入春日、入夏日、入秋日、入冬日。入秋日:连续5日的日平均气温低于22℃,第一天即为入秋日。
如何计算日平均气温呢?
资料
{2D5ABB26-0587-4C30-8999-92F81FD0307C}2时
4时
6时
8时
10时
12时
14时
16时
18时
20时
22时
24时
16
14
14
18
22
24
26
26
22
18
17
16
下面是北京市入秋以来某日的气温情况。(单位:℃)
请你计算北京市这一天的日平均气温。
{2D5ABB26-0587-4C30-8999-92F81FD0307C}2时
4时
6时
8时
10时
12时
14时
16时
18时
20时
22时
24时
16
14
14
18
22
24
26
26
22
18
17
16
下面是北京市入秋以来某日的气温情况。(单位:℃)
(16+18+26+18)÷4
=78÷4
=19.5( ℃ )
答:北京市这一天的日平均气温为19.5 ℃。
{2D5ABB26-0587-4C30-8999-92F81FD0307C}2时
4时
6时
8时
10时
12时
14时
16时
18时
20时
22时
24时
16
14
14
18
22
24
26
26
22
18
17
16
生活中,哪里还有平均数?
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
(1)计算每个班的平均分,排出名次。(结果保留一位小数)
评委
成绩/分
班级
四(1)班:
(92+97+99+97+95)÷5=96.0(分)
四(2)班:
(82+98+98+100+94)÷5=94.4(分)
四(3)班
(89+97+99+98+92)÷5=95.0(分)
96.0>95.0>94.4
四(1)班第1名,四(3)班第2名,四(2)班第3名。
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
(2)如果去掉一个最高分,去掉一个最低分,再计算平均分。(结果保留一位小数)
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
四(1)班:
(97+97+95)÷3≈96.3(分)
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
四(2)班:
(98+98+94)÷3≈96.7(分)
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
四(3)班
(97+98+92)÷3≈95.7(分)
光明小学举办运动会,入场式上要对班级队列进行打分,四年级3个班的评委打分如下:
{5940675A-B579-460E-94D1-54222C63F5DA}?
评委1
评委2
评委3
评委4
评委5
四(1)
92
97
99
97
95
四(2)
82
98
98
100
94
四(3)
89
97
99
98
92
96.7>96.3>95.7
四(2)班第1名,四(1)班第2名,
四(3)班第3名。
四(2)班有一个数据是82分,把平均分拉低了,每个数据都会影响平均分。
两种计算方法,得到的平均分不一样。
平均数在生活中有着广泛的应用。
你的问题得到解决了吗?
选择合适的方法分析数据,根据数据做出判断。
对于同一组数据可以有多种分析方法。
1.数学书第80页第4题。
课后作业
2.数学书第103页第9题。
课后作业
3.继续寻找生活中与平均数有关的实例。
再 见
