青岛(六三)版数学四上 6.快捷的物流运输--解决问题 课件(共16张PPT)
文档属性
| 名称 | 青岛(六三)版数学四上 6.快捷的物流运输--解决问题 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 14:14:29 | ||
图片预览



文档简介
青岛版四年级上册(六·三制)第六单元快捷的物流运输——解决问题
相遇问题
*
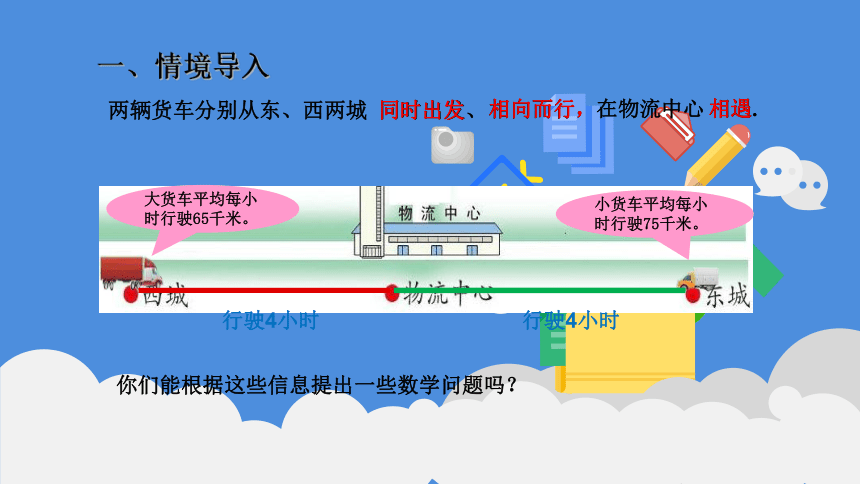
一、情境导入
同时出发、
相向而行,
相遇.
两辆货车分别从东、西两城
在物流中心
同时出发
相向而行,
相遇.
大货车平均每小时行驶65千米。
从图中你能获得哪些数学信息?
小货车平均每小时行驶75千米。
同时出发、
相向而行,
相遇.
两辆货车分别从东、西两城
在物流中心
同时出发
相向而行,
相遇.
大货车平均每小时行驶65千米。
小货车平均每小时行驶75千米。
行驶4小时
行驶4小时
你们能根据这些信息提出一些数学问题吗?
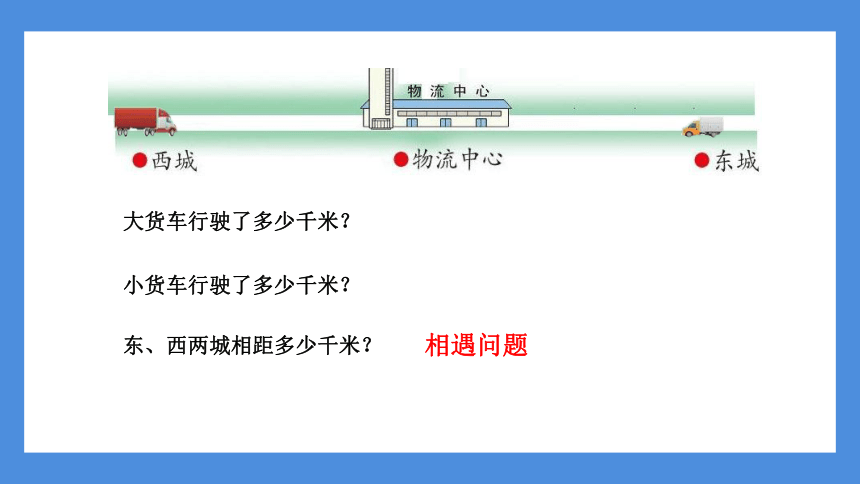
一、情境导入
大货车行驶了多少千米?
小货车行驶了多少千米?
东、西两城相距多少千米?
相遇问题
东、西两城相距多少千米?
同时出发、
相向而行,
相遇.
两辆货车分别从东、西两城
经过4小时在物流中心
同时出发
相向而行,
相遇.
每小时65千米
每小时75千米
?千米
西城
东城
物流中心
大货车平均每小时行驶65千米。
小货车平均每小时行驶75千米。
用自己喜欢的方法把题目中的已知信息和问题整理出来。
4小时相遇
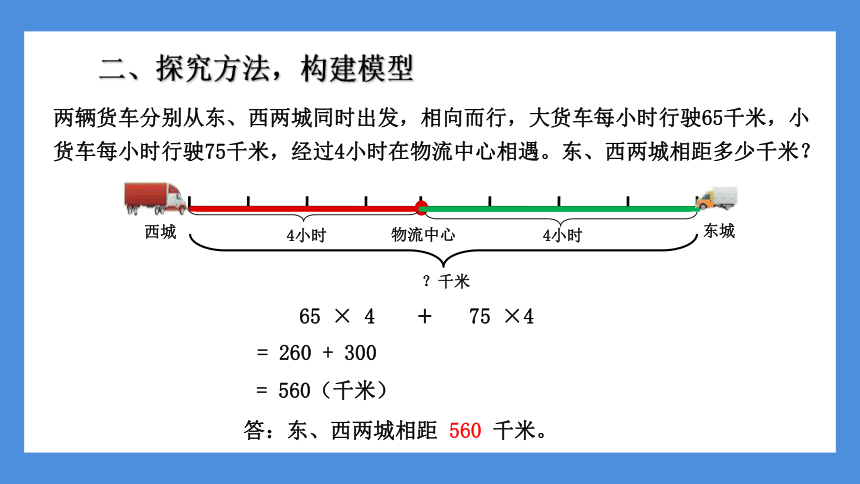
二、探究方法,构建模型
物流中心
4小时
4小时
65 × 4
75 ×4
+
= 260 + 300
答:东、西两城相距 560 千米。
?千米
西城
东城
= 560(千米)
两辆货车分别从东、西两城同时出发,相向而行,大货车每小时行驶65千米,小货车每小时行驶75千米,经过4小时在物流中心相遇。东、西两城相距多少千米?
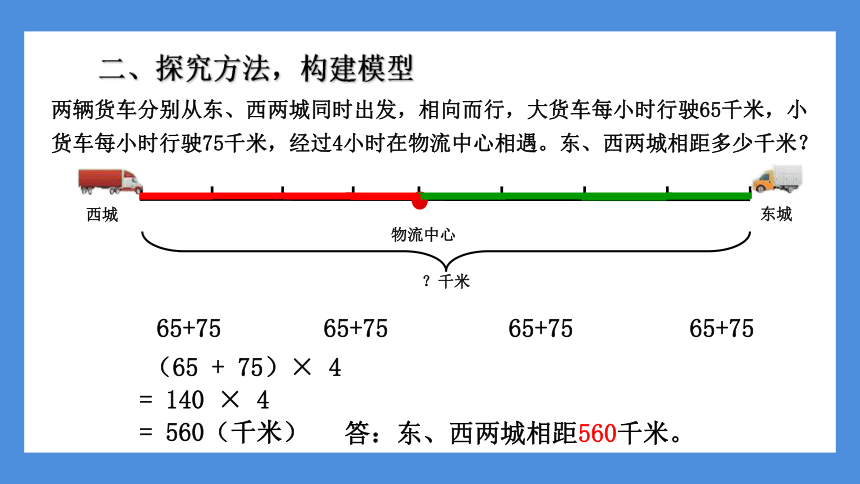
二、探究方法,构建模型
65+75
65+75
65+75
65+75
(65 + 75)× 4
= 140 × 4
= 560(千米)
答:东、西两城相距560千米。
二、探究方法,构建模型
两辆货车分别从东、西两城同时出发,相向而行,大货车每小时行驶65千米,小货车每小时行驶75千米,经过4小时在物流中心相遇。东、西两城相距多少千米?
西城
东城
物流中心
?千米
大货车行驶的路程
+
小货车行驶的路程
= 总路程
速度和
×
时间
= 总路程
回顾上面两种解题思路,想一想,怎样解决相遇问题?
二、探究方法,构建模型
甲
乙
120千米/时
150千米/时
?千米
(150 + 120)×5
= 270 × 5
= 1350(千米)
150 ×5 + 120×5
= 550 + 500
= 1350(千米)
答:东、西两地相距 1350 千米。
1.两列火车分别从东、西两地同时相对开出,甲车每小时行驶150千米,乙车每小时行驶120千米,5小时后相遇。
求东、西两地间的路程。(先画图整理条件和问题,再解答)
三、应用模型,解决问题
5小时相遇
2.
两队分别从两头同时施工,5个月开通。这条隧道长多少米?
(150 + 120)×5
答:这条隧道长 1350米。
= 1350(米)
= 270 × 5
三、应用模型,解决问题
1.两列火车分别从东、西两地同时相对开出,甲车每小时行驶150千米,乙车每小时行驶120千米,5小时后相遇。求东、西两地间的路程。
2.甲乙两队分别从两头同时施工,甲队每月开凿150米,乙队每月开凿120米,5个月开通。这条隧道长多少米?
观察以上两个题的数量关系和列式,你发现了什么?
(150 + 120)×5
(150 + 120)×5
150 ×5 + 120×5
150 ×5 + 120×5
工程问题也能用相遇问题的方法解决。
工程问题的数量关系是:工作效率和×工作时间=工作总量
3.大货车和小货车在物流中心完成了送货和装车打包后两车又同时出发返回到东城和西城,大货车平均每小时行驶65千米,小货车平均每小时行驶75千米。3小时后,两车相距多少千米?
物流中心
3小时
3小时
65 × 3
75 ×3
+
= 195 + 225
答:3小时后,两车相距 420 千米。
西城
东城
= 420(千米)
三、应用模型,解决问题
4.大货车和小货车分别从东、西两城同时出发,相向而行,大货车平均每小时行驶65千米,小货车平均每小时行驶75千米。3小时后两车还相距140千米。东、西两城相距多少千米?(只列式)
物流中心
3小时
3小时
65 × 3 +
75 ×3
= 195 + 140 + 225
答:东、西两城相距 560 千米。
?千米
西城
东城
= 560(千米)
140 +
三、应用模型,解决问题
学会了哪些知识?
获得了哪些方法?
哪个环节最开心?
想一想,两个物体运动,除了上述的情况,还有哪些情况?
五、拓展延伸
谢谢你的观看
相遇问题
*
一、情境导入
同时出发、
相向而行,
相遇.
两辆货车分别从东、西两城
在物流中心
同时出发
相向而行,
相遇.
大货车平均每小时行驶65千米。
从图中你能获得哪些数学信息?
小货车平均每小时行驶75千米。
同时出发、
相向而行,
相遇.
两辆货车分别从东、西两城
在物流中心
同时出发
相向而行,
相遇.
大货车平均每小时行驶65千米。
小货车平均每小时行驶75千米。
行驶4小时
行驶4小时
你们能根据这些信息提出一些数学问题吗?
一、情境导入
大货车行驶了多少千米?
小货车行驶了多少千米?
东、西两城相距多少千米?
相遇问题
东、西两城相距多少千米?
同时出发、
相向而行,
相遇.
两辆货车分别从东、西两城
经过4小时在物流中心
同时出发
相向而行,
相遇.
每小时65千米
每小时75千米
?千米
西城
东城
物流中心
大货车平均每小时行驶65千米。
小货车平均每小时行驶75千米。
用自己喜欢的方法把题目中的已知信息和问题整理出来。
4小时相遇
二、探究方法,构建模型
物流中心
4小时
4小时
65 × 4
75 ×4
+
= 260 + 300
答:东、西两城相距 560 千米。
?千米
西城
东城
= 560(千米)
两辆货车分别从东、西两城同时出发,相向而行,大货车每小时行驶65千米,小货车每小时行驶75千米,经过4小时在物流中心相遇。东、西两城相距多少千米?
二、探究方法,构建模型
65+75
65+75
65+75
65+75
(65 + 75)× 4
= 140 × 4
= 560(千米)
答:东、西两城相距560千米。
二、探究方法,构建模型
两辆货车分别从东、西两城同时出发,相向而行,大货车每小时行驶65千米,小货车每小时行驶75千米,经过4小时在物流中心相遇。东、西两城相距多少千米?
西城
东城
物流中心
?千米
大货车行驶的路程
+
小货车行驶的路程
= 总路程
速度和
×
时间
= 总路程
回顾上面两种解题思路,想一想,怎样解决相遇问题?
二、探究方法,构建模型
甲
乙
120千米/时
150千米/时
?千米
(150 + 120)×5
= 270 × 5
= 1350(千米)
150 ×5 + 120×5
= 550 + 500
= 1350(千米)
答:东、西两地相距 1350 千米。
1.两列火车分别从东、西两地同时相对开出,甲车每小时行驶150千米,乙车每小时行驶120千米,5小时后相遇。
求东、西两地间的路程。(先画图整理条件和问题,再解答)
三、应用模型,解决问题
5小时相遇
2.
两队分别从两头同时施工,5个月开通。这条隧道长多少米?
(150 + 120)×5
答:这条隧道长 1350米。
= 1350(米)
= 270 × 5
三、应用模型,解决问题
1.两列火车分别从东、西两地同时相对开出,甲车每小时行驶150千米,乙车每小时行驶120千米,5小时后相遇。求东、西两地间的路程。
2.甲乙两队分别从两头同时施工,甲队每月开凿150米,乙队每月开凿120米,5个月开通。这条隧道长多少米?
观察以上两个题的数量关系和列式,你发现了什么?
(150 + 120)×5
(150 + 120)×5
150 ×5 + 120×5
150 ×5 + 120×5
工程问题也能用相遇问题的方法解决。
工程问题的数量关系是:工作效率和×工作时间=工作总量
3.大货车和小货车在物流中心完成了送货和装车打包后两车又同时出发返回到东城和西城,大货车平均每小时行驶65千米,小货车平均每小时行驶75千米。3小时后,两车相距多少千米?
物流中心
3小时
3小时
65 × 3
75 ×3
+
= 195 + 225
答:3小时后,两车相距 420 千米。
西城
东城
= 420(千米)
三、应用模型,解决问题
4.大货车和小货车分别从东、西两城同时出发,相向而行,大货车平均每小时行驶65千米,小货车平均每小时行驶75千米。3小时后两车还相距140千米。东、西两城相距多少千米?(只列式)
物流中心
3小时
3小时
65 × 3 +
75 ×3
= 195 + 140 + 225
答:东、西两城相距 560 千米。
?千米
西城
东城
= 560(千米)
140 +
三、应用模型,解决问题
学会了哪些知识?
获得了哪些方法?
哪个环节最开心?
想一想,两个物体运动,除了上述的情况,还有哪些情况?
五、拓展延伸
谢谢你的观看
