华师大版九年级上册24.4解直角三角形课件(共17张ppt)
文档属性
| 名称 | 华师大版九年级上册24.4解直角三角形课件(共17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 745.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 19:33:58 | ||
图片预览


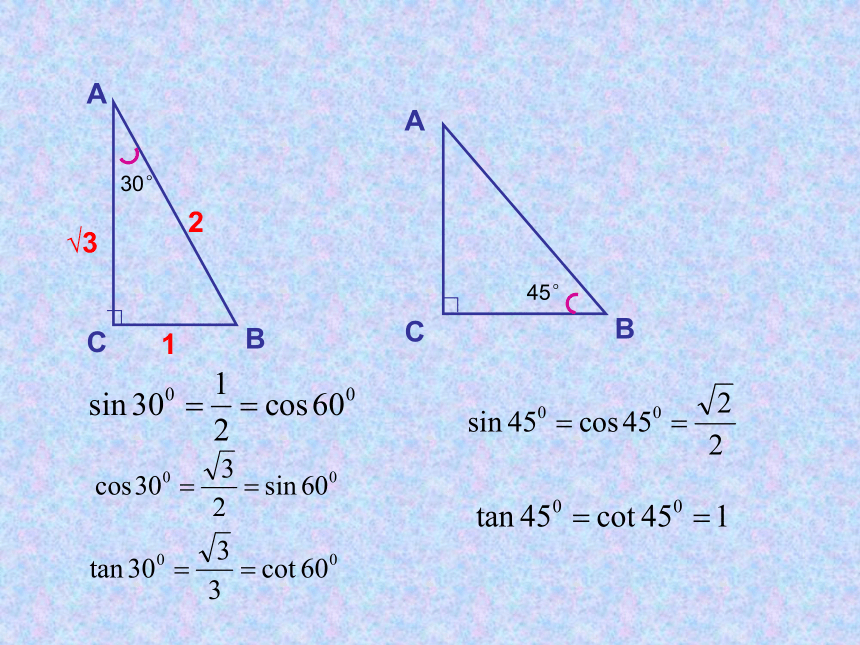

文档简介
(共17张PPT)
24.4
解直角三角形
一、旧知回顾,引入课题
1.直角三角形中,有哪些元素?
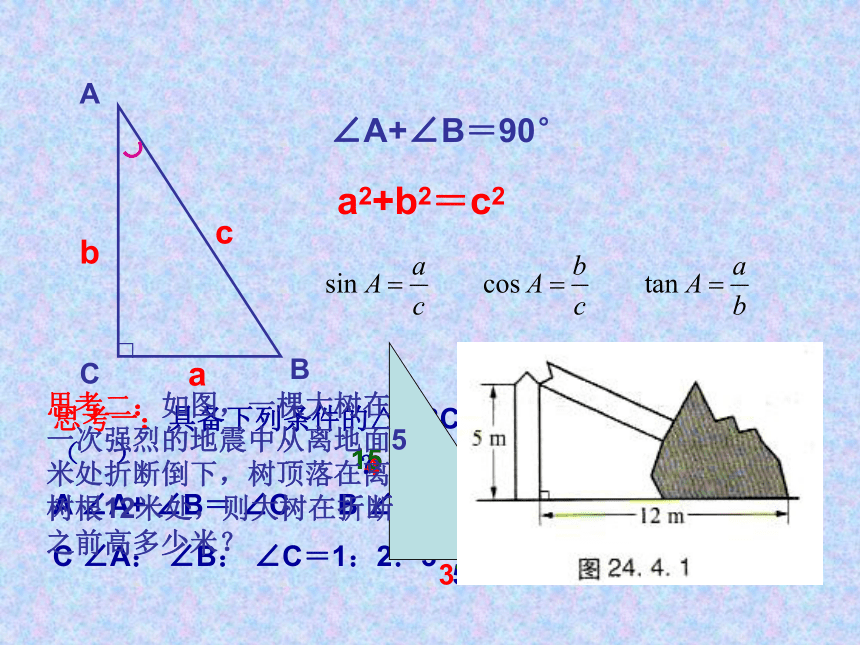
2.直角三角形中的边角关系
A
B
C
∟
∠A+∠B=90°
b
a
c
a2+b2=c2
⌒
思考一:具备下列条件的△ABC,不是直角三角形的是(
)
A
∠A+
∠B=
∠C
B
∠A-
∠B=
∠C
C
∠A:
∠B:
∠C=1:2:3
D
∠A=
∠B=
3∠C
3
4
?
5
13
?
?
15
17
思考二:如图,一棵大树在一次强烈的地震中从离地面5米处折断倒下,树顶落在离树根12米处,则大树在折断之前高多少米?
A
B
C
∟
A
B
C
∟
⌒
⌒
30°
45°
1
2
√3
3.课题引入与解读
(1)解直角三角形
在直角三角形中,由已知元素求未知元素的过程叫做___________
(2)解直角三角形,有哪些类型?
只有两种类型:
①已知两条边,解直角三角形;
②已知一条边和一个锐角,角直角三角形。
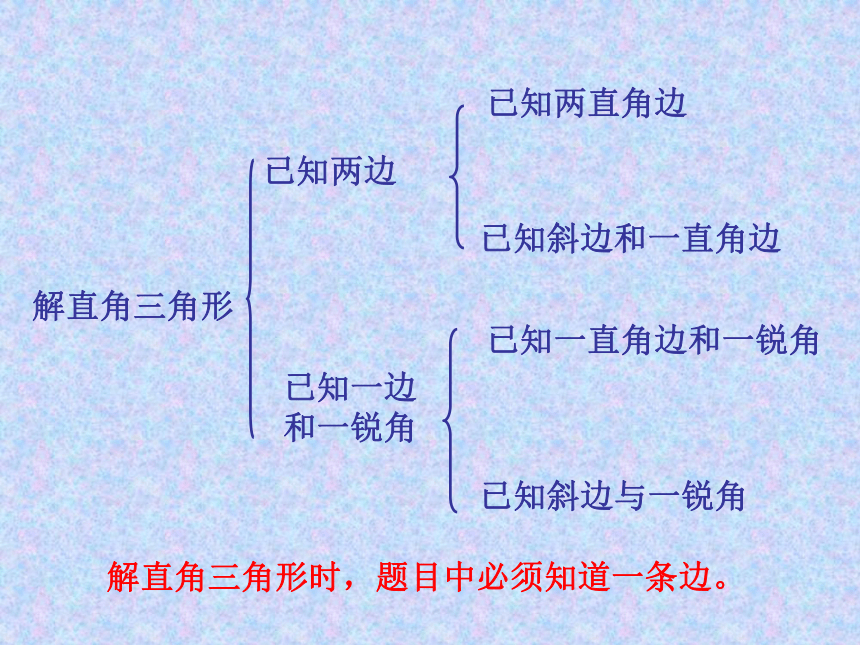
解直角三角形
已知两边
已知一边和一锐角
已知斜边和一直角边
已知两直角边
已知斜边与一锐角
已知一直角边和一锐角
解直角三角形时,题目中必须知道一条边。
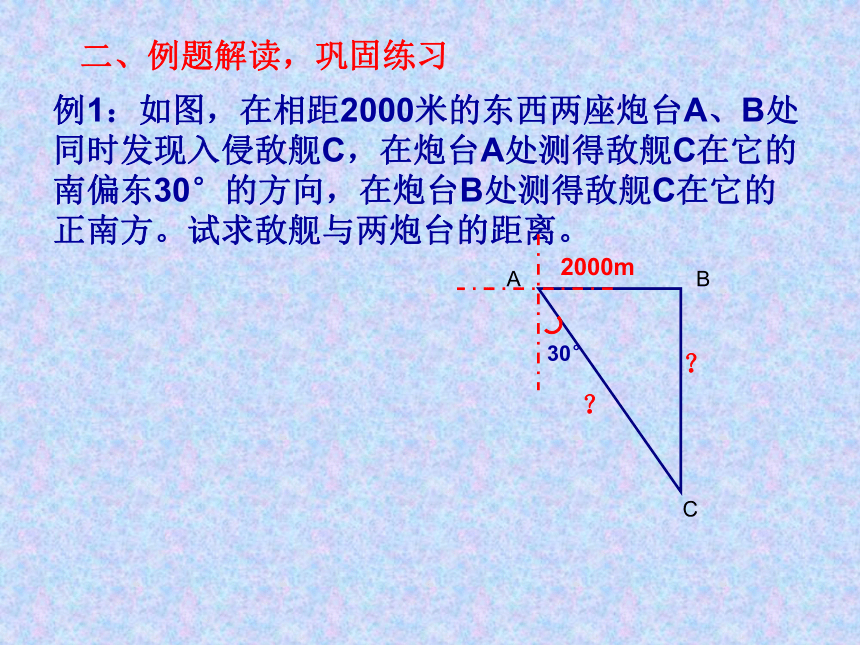
例1:如图,在相距2000米的东西两座炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰C在它的南偏东30°的方向,在炮台B处测得敌舰C在它的正南方。试求敌舰与两炮台的距离。
A
B
C
二、例题解读,巩固练习
⌒
30°
2000m
?
?
思考三:某人从A处出发沿北偏东30°方向走了100米到达B处,再沿北偏西60°方向走了100米到达C处,则他从C处回到A处至少要走______米。
A
B
C
试练:
(1)在电线杆离地面8米处向地面拉一条缆绳,缆绳和地面成60°角,求该缆绳的长及缆绳地面固定点到电线杆底部的距离。
(2)海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船的北偏东30°处,半小时后航行到B处,发现此时灯塔Q与船的距离最短。求灯塔Q到B处的距离。(画出图形后计算,精确到0.1海里)
发现此时灯塔Q在船的北偏东45°
三、拓展延伸,深化知识
1.仰角与俯角
水平线
铅锤线
视线
从下往上看,视线与水平线的夹角——仰角
视线
从上往下看,视线与水平线的夹角——俯角
例3:如图,为了测量旗杆的高度BC,在离旗杆底部10米的A处,用高1.5米的测角仪DA测得旗杆顶端的仰角为60°。求旗杆BC的高。
60°
试练(1)如图,某飞机于空中A处探测到正下方的地面目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角为30°,求A处到控制点B的距离。
2.两座建筑物DA与CB,其地面距离DC为50.4米,从DA的顶点A测得CB顶部B的仰角为30°,测得其底部C的俯角为45°,求这两座建筑物的高。
2.坡度与坡角
B
A
C
D
6m
3m
5m
?m
思考四:根据图中信息,计算梯形ABCD下底AB的长度。
思考五:如图,一堤坝的坡角∠ABC=60°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使坡面的坡角∠ADB=45°,则此时应将坝底向外拓宽多少米(结果保留到0.1米,参考数据根号2取1.414,根号3取1.732)
A
B
C
D
24.4
解直角三角形
一、旧知回顾,引入课题
1.直角三角形中,有哪些元素?
2.直角三角形中的边角关系
A
B
C
∟
∠A+∠B=90°
b
a
c
a2+b2=c2
⌒
思考一:具备下列条件的△ABC,不是直角三角形的是(
)
A
∠A+
∠B=
∠C
B
∠A-
∠B=
∠C
C
∠A:
∠B:
∠C=1:2:3
D
∠A=
∠B=
3∠C
3
4
?
5
13
?
?
15
17
思考二:如图,一棵大树在一次强烈的地震中从离地面5米处折断倒下,树顶落在离树根12米处,则大树在折断之前高多少米?
A
B
C
∟
A
B
C
∟
⌒
⌒
30°
45°
1
2
√3
3.课题引入与解读
(1)解直角三角形
在直角三角形中,由已知元素求未知元素的过程叫做___________
(2)解直角三角形,有哪些类型?
只有两种类型:
①已知两条边,解直角三角形;
②已知一条边和一个锐角,角直角三角形。
解直角三角形
已知两边
已知一边和一锐角
已知斜边和一直角边
已知两直角边
已知斜边与一锐角
已知一直角边和一锐角
解直角三角形时,题目中必须知道一条边。
例1:如图,在相距2000米的东西两座炮台A、B处同时发现入侵敌舰C,在炮台A处测得敌舰C在它的南偏东30°的方向,在炮台B处测得敌舰C在它的正南方。试求敌舰与两炮台的距离。
A
B
C
二、例题解读,巩固练习
⌒
30°
2000m
?
?
思考三:某人从A处出发沿北偏东30°方向走了100米到达B处,再沿北偏西60°方向走了100米到达C处,则他从C处回到A处至少要走______米。
A
B
C
试练:
(1)在电线杆离地面8米处向地面拉一条缆绳,缆绳和地面成60°角,求该缆绳的长及缆绳地面固定点到电线杆底部的距离。
(2)海船以32.6海里/时的速度向正北方向航行,在A处看灯塔Q在海船的北偏东30°处,半小时后航行到B处,发现此时灯塔Q与船的距离最短。求灯塔Q到B处的距离。(画出图形后计算,精确到0.1海里)
发现此时灯塔Q在船的北偏东45°
三、拓展延伸,深化知识
1.仰角与俯角
水平线
铅锤线
视线
从下往上看,视线与水平线的夹角——仰角
视线
从上往下看,视线与水平线的夹角——俯角
例3:如图,为了测量旗杆的高度BC,在离旗杆底部10米的A处,用高1.5米的测角仪DA测得旗杆顶端的仰角为60°。求旗杆BC的高。
60°
试练(1)如图,某飞机于空中A处探测到正下方的地面目标C,此时飞行高度AC=1200米,从飞机上看地面控制点B的俯角为30°,求A处到控制点B的距离。
2.两座建筑物DA与CB,其地面距离DC为50.4米,从DA的顶点A测得CB顶部B的仰角为30°,测得其底部C的俯角为45°,求这两座建筑物的高。
2.坡度与坡角
B
A
C
D
6m
3m
5m
?m
思考四:根据图中信息,计算梯形ABCD下底AB的长度。
思考五:如图,一堤坝的坡角∠ABC=60°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使坡面的坡角∠ADB=45°,则此时应将坝底向外拓宽多少米(结果保留到0.1米,参考数据根号2取1.414,根号3取1.732)
A
B
C
D
