13.1.2 定理与证明-华东师大版八年级数学上册课件(17张)
文档属性
| 名称 | 13.1.2 定理与证明-华东师大版八年级数学上册课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
13.1.2
定理与证明
学习目标
了解基本事实(公理)、定理的概念
(重点)
会用公理、定理进行简单的真命题的证明
(难点)
复习引入
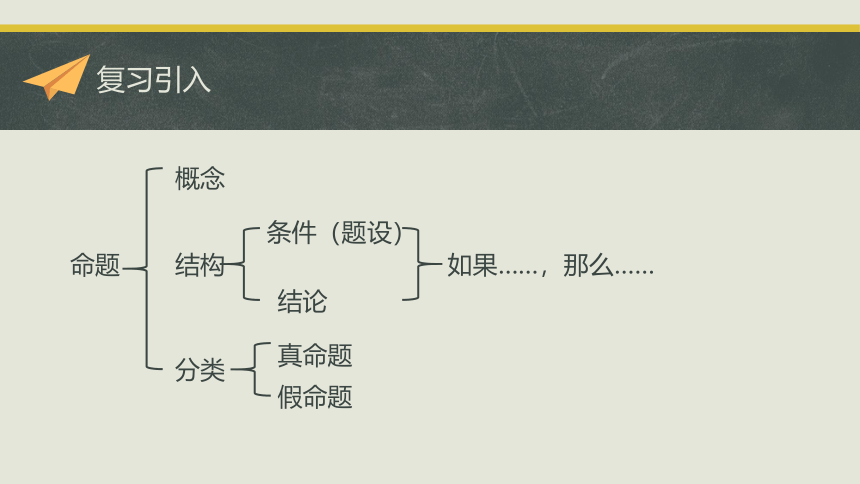
命题
概念
结构
分类
条件(题设)
结论
如果……,那么……
真命题
假命题
新知探究
我们知道下面的命题都是公认的真命题:
两点确定一条直线
;
同一平面内不相交的两条直线互相平行;
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
以上真命题的正确性是人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据,称为公理(基本事实)
新知探究
自主阅读课本,找出定理的概念。
我们学过的定理如:
内错角相等,两直线平行;
过直线外一点有且只有一条直线与该直线平行
你还能再举两个定理的例子吗?
新知探究
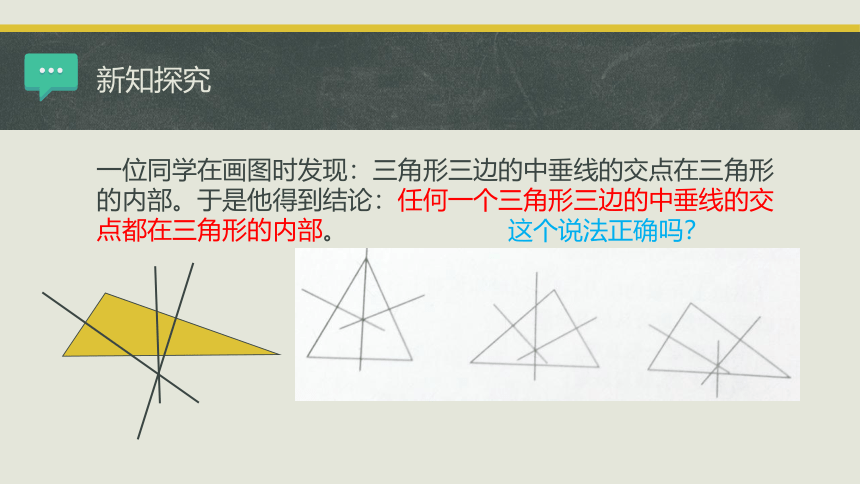
一位同学在画图时发现:三角形三边的中垂线的交点在三角形的内部。于是他得到结论:任何一个三角形三边的中垂线的交点都在三角形的内部。
这个说法正确吗?
新知探究
我们曾经通过计算四边形、五边形、六边形等多边形的内角和,得到一个结论:n边形的内角和等于(n-2)×180°
这个结论正确吗?
正确
新知探究
通过上面几个例子说明:
通过特殊的事例得到的结论可能正确,也可能不正确。
因此:
通过这种方式得到的结论,还需进一步加以证实。
新知探究
自主阅读课本,找出证明的概念。
新知探究
例.
如图,在Rt△ABC中,
已知:∠C=90°
求证:∠A+∠B=90°
A
C
B
新知探究
命题
真命题
假命题
公理
定理
命题、公理和定理的关系
随堂练习
1.把下列命题改写成“如果……,那么……”的形式,指出它的条件和结论,并指出是真命题还是假命题:
(1)同位角相等,两直线平行;
(2)三角形的内角和等于180°;
(3)半径为r的圆的面积为4πr;
(4)四边形的对边平行且相等。
随堂练习
2.判断命题“两条直线被第三条直线所截,同旁内角互补”的真假,如果是假命题,请将其修改为真命题。
假命题。修改为:两条平行直线被第三条直线所截,同旁内角互补。
随堂练习
3.判断命题“小于直角的两个角的和大于直角。”是真命题还是假命题,如果是假命题,请举出反例。
假命题。反例:10°+20°<90°。
课堂小结
命题
真命题
假命题
公理
由实践总结
定理
通过推理证实
举反例
作业布置
同步练习册13.1(二)
数学家名言分享
树老易空,人老易松,科学之道,戒之以空,戒之以松,我愿一辈子从实而终。
——华罗庚
13.1.2
定理与证明
学习目标
了解基本事实(公理)、定理的概念
(重点)
会用公理、定理进行简单的真命题的证明
(难点)
复习引入
命题
概念
结构
分类
条件(题设)
结论
如果……,那么……
真命题
假命题
新知探究
我们知道下面的命题都是公认的真命题:
两点确定一条直线
;
同一平面内不相交的两条直线互相平行;
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行。
以上真命题的正确性是人们在长期实践中总结出来的,并把它们作为判断其他命题真假的原始依据,称为公理(基本事实)
新知探究
自主阅读课本,找出定理的概念。
我们学过的定理如:
内错角相等,两直线平行;
过直线外一点有且只有一条直线与该直线平行
你还能再举两个定理的例子吗?
新知探究
一位同学在画图时发现:三角形三边的中垂线的交点在三角形的内部。于是他得到结论:任何一个三角形三边的中垂线的交点都在三角形的内部。
这个说法正确吗?
新知探究
我们曾经通过计算四边形、五边形、六边形等多边形的内角和,得到一个结论:n边形的内角和等于(n-2)×180°
这个结论正确吗?
正确
新知探究
通过上面几个例子说明:
通过特殊的事例得到的结论可能正确,也可能不正确。
因此:
通过这种方式得到的结论,还需进一步加以证实。
新知探究
自主阅读课本,找出证明的概念。
新知探究
例.
如图,在Rt△ABC中,
已知:∠C=90°
求证:∠A+∠B=90°
A
C
B
新知探究
命题
真命题
假命题
公理
定理
命题、公理和定理的关系
随堂练习
1.把下列命题改写成“如果……,那么……”的形式,指出它的条件和结论,并指出是真命题还是假命题:
(1)同位角相等,两直线平行;
(2)三角形的内角和等于180°;
(3)半径为r的圆的面积为4πr;
(4)四边形的对边平行且相等。
随堂练习
2.判断命题“两条直线被第三条直线所截,同旁内角互补”的真假,如果是假命题,请将其修改为真命题。
假命题。修改为:两条平行直线被第三条直线所截,同旁内角互补。
随堂练习
3.判断命题“小于直角的两个角的和大于直角。”是真命题还是假命题,如果是假命题,请举出反例。
假命题。反例:10°+20°<90°。
课堂小结
命题
真命题
假命题
公理
由实践总结
定理
通过推理证实
举反例
作业布置
同步练习册13.1(二)
数学家名言分享
树老易空,人老易松,科学之道,戒之以空,戒之以松,我愿一辈子从实而终。
——华罗庚
