新疆巴音郭楞蒙古自治州第一中学2020-2021学年初二上学期期中考试数学试卷(word版含答案)
文档属性
| 名称 | 新疆巴音郭楞蒙古自治州第一中学2020-2021学年初二上学期期中考试数学试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 231.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 17:45:00 | ||
图片预览


文档简介
数学
考试时间:100分钟
试卷总分
:100分
一、选择题(每小题3分,满分27分)
题号
1
2
3
4
5
6
7
8
9
选项
1.下列各组线段为边,能组成三角形的是(
)
A.1
cm,
2
cm,4
cm
B.8
cm,6
cm,4
cm
C.12
cm,5
cm,6
cm
D.2
cm,3
cm,6
cm
2.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是(
)
3.
下列说法正确的是(
)
A.全等三角形的对应边相等;
B.面积相等的两个三角形全等;
C.周长相等的两个三角形全等;
D.三对内角分别相等的两个三角形全等;
4.点M(3,2)关于x轴对称的点的坐标为(
)
A.(-3,2)
B.(-3,-2)
C.(3,-2)
D.(2,-3)
5.
如图,在△ABC中,AB=AC,∠A=40°,CD⊥AB于D,
则∠DCB等于(
)
A.70°
B.50°
C.40°
D.20°
6.
等腰三角形的两边长是6cm和3cm,那么它的周长是(
)
A.9cm
B.12
cm
C.12
cm或15
cm
D.15
cm
7.
一个多边形内角和是10800,则这个多边形的边数为
(
)
A.
6
B.
7
C.
8
D.
9
8.
若△ABC≌△DEF,∠A=80°,∠B=40°,那么∠F的度数是(
)
A.80°
B.40°
C.60°
D.120°
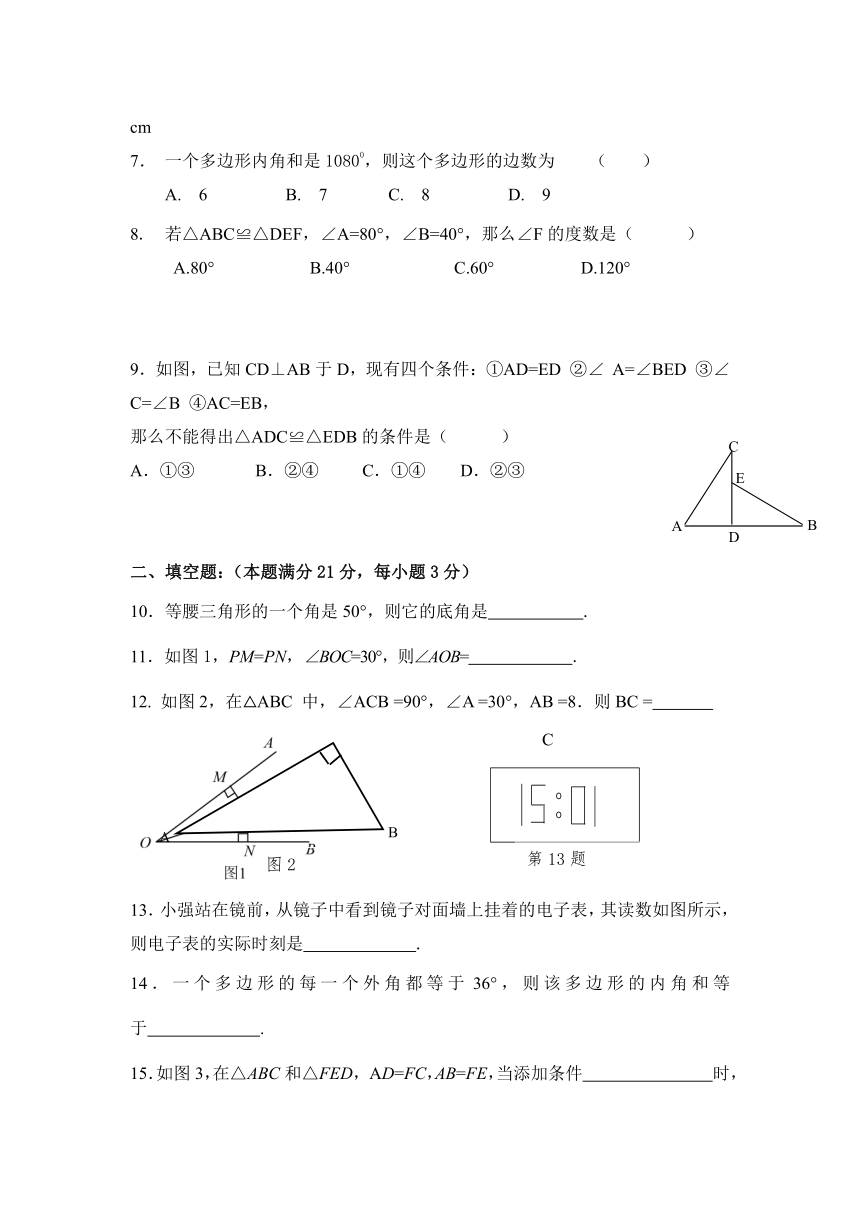
9.如图,已知CD⊥AB于D,现有四个条件:①AD=ED
②∠
A=∠BED
③∠C=∠B
④AC=EB,
那么不能得出△ADC≌△EDB的条件是(
)
A.①③
B.②④
C.①④
D.②③
二、填空题:(本题满分21分,每小题3分)
10.等腰三角形的一个角是50°,则它的底角是
.
11.如图1,PM=PN,∠BOC=30°,则∠AOB=
.
12.
如图2,在△ABC
中,∠ACB
=90°,∠A
=30°,AB
=8.则BC
=
13.小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是
.
14.一个多边形的每一个外角都等于36°,则该多边形的内角和等于
.
15.如图3,在△ABC和△FED,
AD=FC,AB=FE,当添加条件
时,就可得到△ABC
≌△FED.(只需填写一个你认为正确的条件)
16.
如图,在△ABC中,AB=5,AC=3,BC的垂直平分线交AB于D,
交BC于E,
则△ADC的周长等于
.
三、作图题:(共14分)
17.(6分)如图:已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB
两边的距离相等(不写作法,保留作图痕迹).
18.(8分)如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点
A1,B1,C1的坐标:A1
,B1
,C1
;
(3)求△A1B1C1
的面积;
四、解答题:(共13分)
19.(6分)如图,AB∥CD,∠D=65°,∠B=36°,求∠E的度数.
(7分)一个多边形内角和比其外角和的2倍多180°,求这个多边形的边数.
五、证明题:(共25分)
21.(7分)如图,已知AE=CF,AD=CB,AD∥CB,求证:DF∥BE
22.(9分)如图,在△ABC
中,D是BC的中点,DE⊥AB,DF⊥AC,垂足
分别是E、F,且BE=CF.求证:AD平分∠BAC.
23.
(9分)如图,△ABD,△AEC都是等边三角形,求证:BE=DC.
答案
一、选择题:
1-5:BAACD
6-9:DCCD
二、填空题
10.
50°或65°
11.
4
12.
60°
13.
10:21
14.
1440
15.BC=DE或∠BAC=∠DFE
或AB∥EF(答案不唯一)
16.
8
三、作图题
17.(6分)
18.
(10分)
解:(1)
△A1B1C1如图所示
(注:没有虚线)
(2)A1
(3,2);B1
(4,-3);C1
(1,-1)
(3)解:△A1B1C1的面积=3×5-×2×3-×1×5-×2×3=6.5
四:解答题(共13分)
19.(6分).
解:设ED和AB的交点为F
∵AB∥CD,∠D=65°,
∴∠AFE=∠D=65°(两直线平行,同位角相等),
∵∠AFE是△BEF的外角,∠B=36°,
∴∠E=∠AFE?∠B=65°?36°=29°
答:∠E为29°
------------------
(6分)
20.(7分)
解:设这个多边形的边数为n,
根据题意,得(n-2)×180°=2×360°+180°,
解得n=7.
故这个多边形的边数是7.(7分)
五、证明题(共23分)
21.(7分)
证明:∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE
又∵CB∥AD
∴∠A=∠C
在△ADF和△EBC中,
∴△ADF≌△EBC
(SAS).
∴∠DFE=∠BEF.
∴
DF∥BE
22.
(7分)
证明:∵DE⊥AB,DF⊥AC
∴∠BED=∠DFC=90°
∵D是BC的中点
∴BD=CD(中点的性质)
∴在△BDE和△CDF中
∴△BDE≌△CDF(HL)
∴DE=DF(角平分线上的点到角的两边距离相等)
∴AD平分∠BAC.
23.(9分)
证明:在等边△ABD中,有AD=AB,且∠baiDAB=60度
在等边△AEC中,有AC=AE,且∠EAC=60度
所以du∠zhiDAB=∠EAC
通过图可知:
∠DAC=∠DAB+∠BAC
∠BAE=∠EAC+∠BAC
所以∠DAC=∠BAE
于是:在△DAC和△BAE中:
AD=AB,AC=AE,∠DAC=∠BAE
由“边角边”可得出:
△DAC全等于△BAE
于是CD=BE
考试时间:100分钟
试卷总分
:100分
一、选择题(每小题3分,满分27分)
题号
1
2
3
4
5
6
7
8
9
选项
1.下列各组线段为边,能组成三角形的是(
)
A.1
cm,
2
cm,4
cm
B.8
cm,6
cm,4
cm
C.12
cm,5
cm,6
cm
D.2
cm,3
cm,6
cm
2.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是(
)
3.
下列说法正确的是(
)
A.全等三角形的对应边相等;
B.面积相等的两个三角形全等;
C.周长相等的两个三角形全等;
D.三对内角分别相等的两个三角形全等;
4.点M(3,2)关于x轴对称的点的坐标为(
)
A.(-3,2)
B.(-3,-2)
C.(3,-2)
D.(2,-3)
5.
如图,在△ABC中,AB=AC,∠A=40°,CD⊥AB于D,
则∠DCB等于(
)
A.70°
B.50°
C.40°
D.20°
6.
等腰三角形的两边长是6cm和3cm,那么它的周长是(
)
A.9cm
B.12
cm
C.12
cm或15
cm
D.15
cm
7.
一个多边形内角和是10800,则这个多边形的边数为
(
)
A.
6
B.
7
C.
8
D.
9
8.
若△ABC≌△DEF,∠A=80°,∠B=40°,那么∠F的度数是(
)
A.80°
B.40°
C.60°
D.120°
9.如图,已知CD⊥AB于D,现有四个条件:①AD=ED
②∠
A=∠BED
③∠C=∠B
④AC=EB,
那么不能得出△ADC≌△EDB的条件是(
)
A.①③
B.②④
C.①④
D.②③
二、填空题:(本题满分21分,每小题3分)
10.等腰三角形的一个角是50°,则它的底角是
.
11.如图1,PM=PN,∠BOC=30°,则∠AOB=
.
12.
如图2,在△ABC
中,∠ACB
=90°,∠A
=30°,AB
=8.则BC
=
13.小强站在镜前,从镜子中看到镜子对面墙上挂着的电子表,其读数如图所示,则电子表的实际时刻是
.
14.一个多边形的每一个外角都等于36°,则该多边形的内角和等于
.
15.如图3,在△ABC和△FED,
AD=FC,AB=FE,当添加条件
时,就可得到△ABC
≌△FED.(只需填写一个你认为正确的条件)
16.
如图,在△ABC中,AB=5,AC=3,BC的垂直平分线交AB于D,
交BC于E,
则△ADC的周长等于
.
三、作图题:(共14分)
17.(6分)如图:已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB
两边的距离相等(不写作法,保留作图痕迹).
18.(8分)如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).
(1)在图中作出△ABC关于y轴对称的△A1B1C1;
(2)写出点
A1,B1,C1的坐标:A1
,B1
,C1
;
(3)求△A1B1C1
的面积;
四、解答题:(共13分)
19.(6分)如图,AB∥CD,∠D=65°,∠B=36°,求∠E的度数.
(7分)一个多边形内角和比其外角和的2倍多180°,求这个多边形的边数.
五、证明题:(共25分)
21.(7分)如图,已知AE=CF,AD=CB,AD∥CB,求证:DF∥BE
22.(9分)如图,在△ABC
中,D是BC的中点,DE⊥AB,DF⊥AC,垂足
分别是E、F,且BE=CF.求证:AD平分∠BAC.
23.
(9分)如图,△ABD,△AEC都是等边三角形,求证:BE=DC.
答案
一、选择题:
1-5:BAACD
6-9:DCCD
二、填空题
10.
50°或65°
11.
4
12.
60°
13.
10:21
14.
1440
15.BC=DE或∠BAC=∠DFE
或AB∥EF(答案不唯一)
16.
8
三、作图题
17.(6分)
18.
(10分)
解:(1)
△A1B1C1如图所示
(注:没有虚线)
(2)A1
(3,2);B1
(4,-3);C1
(1,-1)
(3)解:△A1B1C1的面积=3×5-×2×3-×1×5-×2×3=6.5
四:解答题(共13分)
19.(6分).
解:设ED和AB的交点为F
∵AB∥CD,∠D=65°,
∴∠AFE=∠D=65°(两直线平行,同位角相等),
∵∠AFE是△BEF的外角,∠B=36°,
∴∠E=∠AFE?∠B=65°?36°=29°
答:∠E为29°
------------------
(6分)
20.(7分)
解:设这个多边形的边数为n,
根据题意,得(n-2)×180°=2×360°+180°,
解得n=7.
故这个多边形的边数是7.(7分)
五、证明题(共23分)
21.(7分)
证明:∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE
又∵CB∥AD
∴∠A=∠C
在△ADF和△EBC中,
∴△ADF≌△EBC
(SAS).
∴∠DFE=∠BEF.
∴
DF∥BE
22.
(7分)
证明:∵DE⊥AB,DF⊥AC
∴∠BED=∠DFC=90°
∵D是BC的中点
∴BD=CD(中点的性质)
∴在△BDE和△CDF中
∴△BDE≌△CDF(HL)
∴DE=DF(角平分线上的点到角的两边距离相等)
∴AD平分∠BAC.
23.(9分)
证明:在等边△ABD中,有AD=AB,且∠baiDAB=60度
在等边△AEC中,有AC=AE,且∠EAC=60度
所以du∠zhiDAB=∠EAC
通过图可知:
∠DAC=∠DAB+∠BAC
∠BAE=∠EAC+∠BAC
所以∠DAC=∠BAE
于是:在△DAC和△BAE中:
AD=AB,AC=AE,∠DAC=∠BAE
由“边角边”可得出:
△DAC全等于△BAE
于是CD=BE
同课章节目录
