人教版八年级数学下册课件:19.3 课题学习 选择方案(25张)
文档属性
| 名称 | 人教版八年级数学下册课件:19.3 课题学习 选择方案(25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 20:25:19 | ||
图片预览





文档简介
(共25张PPT)
第十九章
一次函数
19.3
课题学习
选择方案
知识回顾
1.一次函数y1=4x+5与y2=3x+10的图象如图所示,
当x=_____时,y1=y2,
当x______时,y1>y2
当x______时,y1>5
<5
5
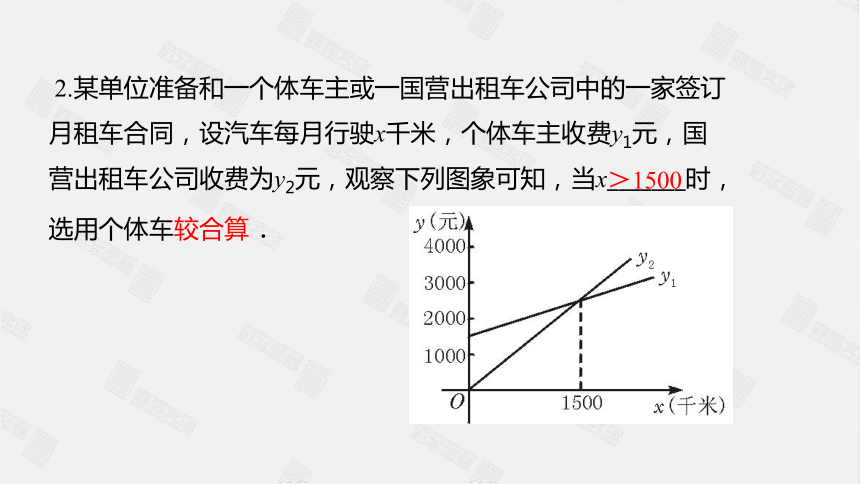
2.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x_______时,选用个体车较合算.
>1500
情景导入
一件事情,有时会有不同的实施方案
A
方案
B
方案
C
方案
D
方案
选择方案时,常用到一次函数选择最优方案
获取新知
问题1
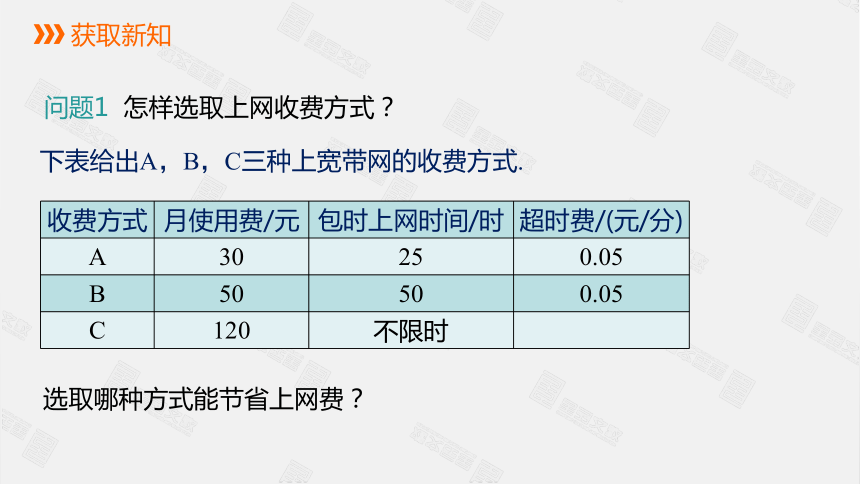
怎样选取上网收费方式?
收费方式
月使用费/元
包时上网时间/时
超时费/(元/分)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
下表给出A,B,C三种上宽带网的收费方式.
选取哪种方式能节省上网费?
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
收费方式
月使用费/元
包时上网时间/时
超时费/(元/分)
A
30
25
0.05
B
50
50
0.05
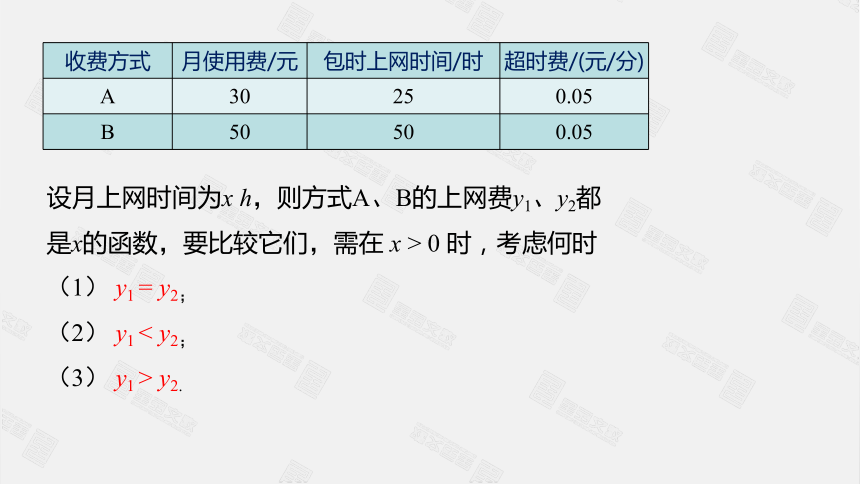
设月上网时间为x
h,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在
x
>
0
时,考虑何时
(1)
y1
=
y2;
(2)
y1
<
y2;
(3)
y1
>
y2.
收费方式
月使用费/元
包时上网时间/时
超时费/(元/分)
A
30
25
0.05
在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
不一定,只有在上网时间超过25小时时才会产生.
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
当x≥0时,y3=120.
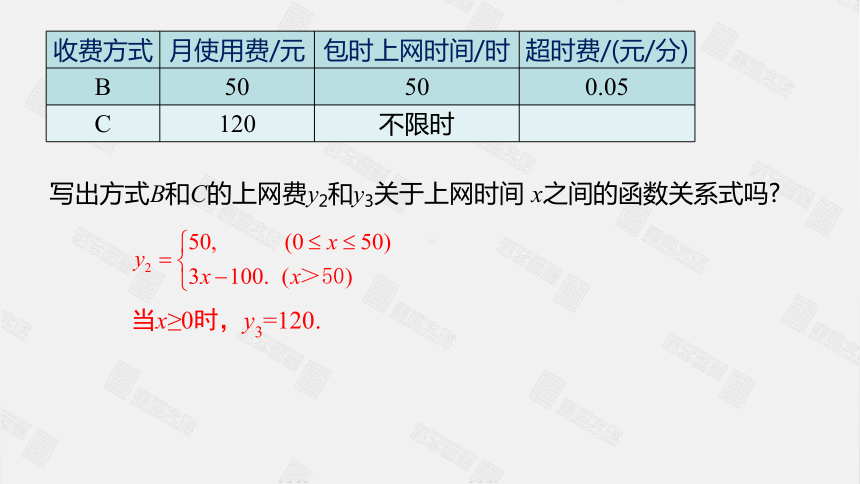
写出方式B和C的上网费y2和y3关于上网时间
x之间的函数关系式吗?
收费方式
月使用费/元
包时上网时间/时
超时费/(元/分)
B
50
50
0.05
C
120
不限时
方式A.
在同一坐标系画出它们的图象:
方式B.
方式C.
当x≥0时,y3=120.
当上网时__________时,选择方式A最省钱.
在同一坐标系画出它们的图象:
此时,A和B方式一样省钱
当上网时__________时,选择方式A最省钱.
当上网时间____________时,选择方式B最省钱.
在同一坐标系画出它们的图象:
此时,B和C方式一样省钱
当上网时__________时,选择方式A最省钱.
当上网时间__________时,选择方式B最省钱.
当上网时间_________时,选择方式C最省钱.
在同一坐标系画出它们的图象:
问题2
怎样租车?
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
分析(1)影响最后的租车费用的因素有哪些?
主要影响因素是甲、乙两种车所租辆数.
(2)汽车所租辆数又与哪些因素有关?
与乘车人数有关.
(3)如何由乘车人数确定租车辆数呢?
①要保证240名师生都有车坐,汽车总数不能小于6
辆;
②要使每辆汽车上至少有1
名教师,汽车总数不能大于6辆.
(4)在汽车总数确定后,租车费用与租车的种类
有关.如果租甲类车x
辆,能求出租车费用吗?
设租用
x
辆甲种客车,则租用乙种客车的辆数为(6-x)辆;
设租车费用为
y,则y
=400x+280(6-x)化简得y
=120x+1
680.
①为使240
名师生有车坐,则
45x+30(6-x)≥240;
②为使租车费用不超过2
300
元,则
400x+280(6-x)≤2
300.
(5)如何确定
y
=120x+1
680中
y
的最小值.
由 ,得
.
据实际意义可取4
或5;
因为
y
随着
x
的增大而增大,所以当
x
=4
时,y
最小,y
的最小值为2
160.
解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
总结归纳
随堂演练
1.某化妆品公司每月付给销售人员的工资有两种方案:
方案一:没有底薪,只拿销售提成;
方案二:底薪加销售提成.
设x(件)是销售商品的数量,y(元)是销售人员的月工资,如图,y1为方案一的函数图象,y2为方案二的函数图象.根据图中信息解答如下问题:
(1)方案一中每件商品的提成是____元;
方案二中每件商品的提成是___元.
(2)点A的坐标为____________.
(3)如果销售人员小丽这个月销售了600件商品,那么她采用方案_____获得的报酬会更多一些.
14
7
(300,5600)
一
2.甲、乙两商场以同样的价格出售同样的商品,但各自推出不同的优惠方案:在甲商场累计购物超过100元后,超过100元的部分按80%收费;在乙商场累计购物超过50元后,超过50元的部分按90%收费.设小红在同一商场累计购物x(x>100)元,她在甲商场购物实际付费y1元,在乙商场购物实际付费y2元.
(1)分别求y1,y2,与x之间的函数解析式;
(2)随着小红累计购物金额的变化,分析她在哪家商场购物更合算.
解:(1)由题意得,y1=100+(x-100)×80%=0.8x+20(x>100),
y2=50+(x-50)×90%=0.9x+5(x>100).
(2)当y1>y2时,0.8x+20>0.9x+5,
解得x<150;
当y1=y2时,0.8x+20=0.9x+5,
解得x=150;
当y1解得x>150.
答:当小红累计购物150元时,在两商场实际付费相同;当累计购物超过150元时,在甲商场购物合算;当累计购物大于100元但小于150元时,在乙商场购物合算.
3..某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个.若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元;
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
解:(1)设直拍球拍每副x元,横拍球拍每副y元,
由题意,得
解得
答:直拍球拍每副220元,横拍球拍每副260元.
(2)设购买直拍球拍m副,则购买横拍球拍(40-m)副.
由题意,得m≤3(40-m),解得m≤30.
设买40副球拍所需的费用为w元,
则w=(220+20)m+(260+20)(40-m)=-40m+11200.
因为-40<0,
所以w随m的增大而减小,
所以当m=30时,w取得最小值,最小值为-40×30+11200=10000(元).
此时40-m=40-30=10.
答:购买直拍球拍30副,横拍球拍10副时,费用最少,为10000元.
课堂小结
解决方案问题步骤:
1.把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).
2.通过解不等式或画函数图象的方式确定自变量的范围.
3.利用一次函数的增减性知识从而选择出最佳方案.
第十九章
一次函数
19.3
课题学习
选择方案
知识回顾
1.一次函数y1=4x+5与y2=3x+10的图象如图所示,
当x=_____时,y1=y2,
当x______时,y1>y2
当x______时,y1
<5
5
2.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x_______时,选用个体车较合算.
>1500
情景导入
一件事情,有时会有不同的实施方案
A
方案
B
方案
C
方案
D
方案
选择方案时,常用到一次函数选择最优方案
获取新知
问题1
怎样选取上网收费方式?
收费方式
月使用费/元
包时上网时间/时
超时费/(元/分)
A
30
25
0.05
B
50
50
0.05
C
120
不限时
下表给出A,B,C三种上宽带网的收费方式.
选取哪种方式能节省上网费?
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
收费方式
月使用费/元
包时上网时间/时
超时费/(元/分)
A
30
25
0.05
B
50
50
0.05
设月上网时间为x
h,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在
x
>
0
时,考虑何时
(1)
y1
=
y2;
(2)
y1
<
y2;
(3)
y1
>
y2.
收费方式
月使用费/元
包时上网时间/时
超时费/(元/分)
A
30
25
0.05
在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
不一定,只有在上网时间超过25小时时才会产生.
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
当x≥0时,y3=120.
写出方式B和C的上网费y2和y3关于上网时间
x之间的函数关系式吗?
收费方式
月使用费/元
包时上网时间/时
超时费/(元/分)
B
50
50
0.05
C
120
不限时
方式A.
在同一坐标系画出它们的图象:
方式B.
方式C.
当x≥0时,y3=120.
当上网时__________时,选择方式A最省钱.
在同一坐标系画出它们的图象:
此时,A和B方式一样省钱
当上网时__________时,选择方式A最省钱.
当上网时间____________时,选择方式B最省钱.
在同一坐标系画出它们的图象:
此时,B和C方式一样省钱
当上网时__________时,选择方式A最省钱.
当上网时间__________时,选择方式B最省钱.
当上网时间_________时,选择方式C最省钱.
在同一坐标系画出它们的图象:
问题2
怎样租车?
某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆汽车上至少有1名教师.现有甲、乙两种大客车,它们的载客量和租金如表所示:
(1)共需租多少辆汽车?
(2)给出最节省费用的租车方案.
甲种客车
乙种客车
载客量(单位:人/辆)
45
30
租金
(单位:元/辆)
400
280
分析(1)影响最后的租车费用的因素有哪些?
主要影响因素是甲、乙两种车所租辆数.
(2)汽车所租辆数又与哪些因素有关?
与乘车人数有关.
(3)如何由乘车人数确定租车辆数呢?
①要保证240名师生都有车坐,汽车总数不能小于6
辆;
②要使每辆汽车上至少有1
名教师,汽车总数不能大于6辆.
(4)在汽车总数确定后,租车费用与租车的种类
有关.如果租甲类车x
辆,能求出租车费用吗?
设租用
x
辆甲种客车,则租用乙种客车的辆数为(6-x)辆;
设租车费用为
y,则y
=400x+280(6-x)化简得y
=120x+1
680.
①为使240
名师生有车坐,则
45x+30(6-x)≥240;
②为使租车费用不超过2
300
元,则
400x+280(6-x)≤2
300.
(5)如何确定
y
=120x+1
680中
y
的最小值.
由 ,得
.
据实际意义可取4
或5;
因为
y
随着
x
的增大而增大,所以当
x
=4
时,y
最小,y
的最小值为2
160.
解决含有多个变量的问题时,可以分析这些变量之间的关系,从中选取一个取值能影响其他变量的值的变量作为自变量,然后根据问题的条件寻求可以反映实际问题的函数,以此作为解决问题的数学模型.
总结归纳
随堂演练
1.某化妆品公司每月付给销售人员的工资有两种方案:
方案一:没有底薪,只拿销售提成;
方案二:底薪加销售提成.
设x(件)是销售商品的数量,y(元)是销售人员的月工资,如图,y1为方案一的函数图象,y2为方案二的函数图象.根据图中信息解答如下问题:
(1)方案一中每件商品的提成是____元;
方案二中每件商品的提成是___元.
(2)点A的坐标为____________.
(3)如果销售人员小丽这个月销售了600件商品,那么她采用方案_____获得的报酬会更多一些.
14
7
(300,5600)
一
2.甲、乙两商场以同样的价格出售同样的商品,但各自推出不同的优惠方案:在甲商场累计购物超过100元后,超过100元的部分按80%收费;在乙商场累计购物超过50元后,超过50元的部分按90%收费.设小红在同一商场累计购物x(x>100)元,她在甲商场购物实际付费y1元,在乙商场购物实际付费y2元.
(1)分别求y1,y2,与x之间的函数解析式;
(2)随着小红累计购物金额的变化,分析她在哪家商场购物更合算.
解:(1)由题意得,y1=100+(x-100)×80%=0.8x+20(x>100),
y2=50+(x-50)×90%=0.9x+5(x>100).
(2)当y1>y2时,0.8x+20>0.9x+5,
解得x<150;
当y1=y2时,0.8x+20=0.9x+5,
解得x=150;
当y1
答:当小红累计购物150元时,在两商场实际付费相同;当累计购物超过150元时,在甲商场购物合算;当累计购物大于100元但小于150元时,在乙商场购物合算.
3..某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个.若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元;
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
解:(1)设直拍球拍每副x元,横拍球拍每副y元,
由题意,得
解得
答:直拍球拍每副220元,横拍球拍每副260元.
(2)设购买直拍球拍m副,则购买横拍球拍(40-m)副.
由题意,得m≤3(40-m),解得m≤30.
设买40副球拍所需的费用为w元,
则w=(220+20)m+(260+20)(40-m)=-40m+11200.
因为-40<0,
所以w随m的增大而减小,
所以当m=30时,w取得最小值,最小值为-40×30+11200=10000(元).
此时40-m=40-30=10.
答:购买直拍球拍30副,横拍球拍10副时,费用最少,为10000元.
课堂小结
解决方案问题步骤:
1.把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).
2.通过解不等式或画函数图象的方式确定自变量的范围.
3.利用一次函数的增减性知识从而选择出最佳方案.
