人教版八年级数学下册20.1.1 平均数课件(第1课时 共23张PPT)
文档属性
| 名称 | 人教版八年级数学下册20.1.1 平均数课件(第1课时 共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 19:51:09 | ||
图片预览







文档简介
(共23张PPT)
第二十章
数据的分析
20.1.1
第1课时
平均数
情景导入
据资料记载,位于意大利的比萨斜塔1918-1958
这41年间,平均每年倾斜1.10毫米;1959-1969这11年
间,平均每年倾斜1.26毫米,
那么1918-1969这52年间,你
知道比萨斜塔平均每年倾斜
约多少毫米吗?(精确到
0.01毫米).
获取新知
知识点一:加权平均数-权表示重要性
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应试者进行了听、说、读、写、的英语水平测试,他们的各项成绩如表所示:
(1)如果公司想招一名综合能力较强的翻译,请计算两名应试者的平均成绩,应该录用谁?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
(1)如果这家公司想招一名综合能力较强的翻译,计算两名应试者的平均成绩.从他们的成绩看,应该录取谁?
乙的平均成绩为
解:
甲的平均成绩为
,
算术平均数
算术平均数
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
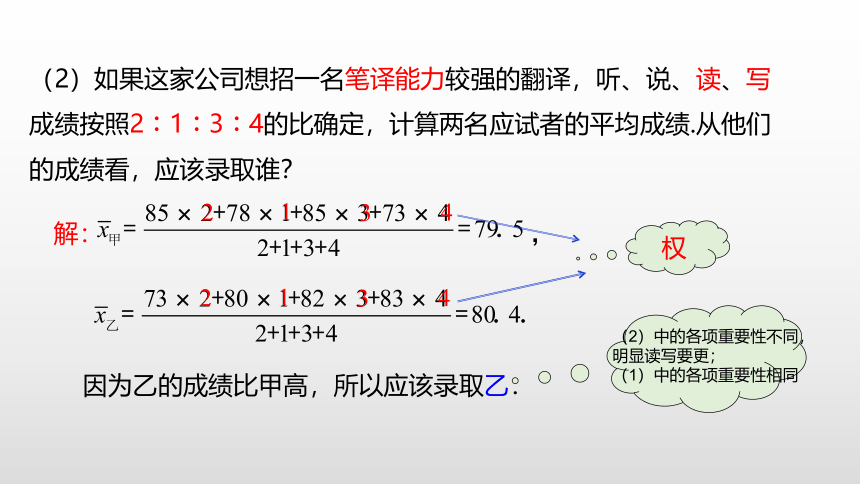
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2︰1︰3︰4的比确定,计算两名应试者的平均成绩.从他们的成绩看,应该录取谁?
解:
,
4
3
1
2
4
3
1
2
权
因为乙的成绩比甲高,所以应该录取乙.
(2)中的各项重要性不同,明显读写要更;
(1)中的各项重要性相同
一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则
叫做这n个数的加权平均数.
思考
如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照
3︰3︰2︰2
的比例确定,那么甲、乙两人谁将被录取?与上述问题中的(1)(2)相比较,你能体会到权的作用吗?
权有重要程度的作用.
甲将被录取.
例题讲解
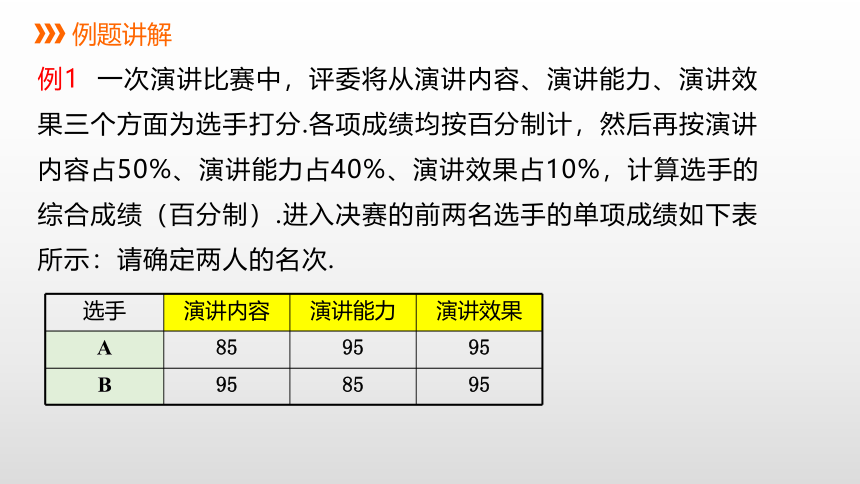
例1
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制计,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:请确定两人的名次.
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
解:选手A的最后得分是
选手B的最后得分是
由上可知选手B获得第一名,选手A获得第二名.
权的常见形式:比值或百分数
获取新知
知识点二:加权平均数-权表示频数
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的加权平均数,
其中f1,f2,…,fk分别叫做x1,x2,…,xk的权.
算术平均数与加权平均数的区别和联系
2.在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数,当各项权相等时,计算平均数就要采用算术平均数.
1.算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等);
这里的权,包含了“重要性”或频次两种
探究
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少?
载客量/人
频数(班次)
1≤x<21
3
21
≤x<41
5
41
≤x<61
20
61
≤x<81
22
81
≤x<101
18
101
≤x<121
15
1.数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
载客量/人
组中值
频数(班次)
1≤x<21
11
3
21
≤x<41
31
5
41
≤x<61
51
20
61
≤x<81
71
22
81
≤x<101
91
18
101
≤x<121
111
15
2.根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
解:这天5路公共汽车平均每班的载客量是
例题讲解
例2
某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数).
解:这个跳水队运动员的平均年龄为:
8
16
24
2
≈14(岁).
答:这个跳水队运动员的平均年龄约为14岁.
随堂演练
1.
7名学生的体重(单位:
kg)分别是40,42,43,45,47,47,58,则这组数据的平均数是( )A.44
B.45
C.46
D.47
C
2.
小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分
C.84.5分
D.86分
D
3.
从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A.
B.
C.
D.
B
4.
睡眠是评价人类健康水平的一项重要指标,充足的睡眠是青少年健康成长的必要条件之一.小强同学通过问卷调查的方式了解到本班三名同学某天的睡眠时间分别为7.8小时,8.6小时,8.8小时,则这三名同学该天的平均睡眠时间是______小时.
8.4
5.
某班40名学生的某次数学测验成绩统计如下表:
成绩(分)
50
60
70
80
90
100
人数(人)
2
x
10
y
4
2
若这个班该次数学测验的平均成绩是69分,则x=____,y=____.
18
4
6.
某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示,综合成绩按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,求被录取教师的综合成绩.
教师
成绩
甲
乙
丙
笔试
80分
82分
78分
面试
76分
74分
78分
解:甲的综合成绩为80×60%+76×40%=78.4(分),
乙的综合成绩为82×60%+74×40%=78.8(分),
丙的综合成绩为78×60%+78×40%=78(分).
因为78<78.4<78.8,
所以被录取的教师为乙,其综合成绩为78.8分.
课堂小结
平均数与加权平均数
加权平均数:
算术平均数:
“重要”型
“频次”型
第二十章
数据的分析
20.1.1
第1课时
平均数
情景导入
据资料记载,位于意大利的比萨斜塔1918-1958
这41年间,平均每年倾斜1.10毫米;1959-1969这11年
间,平均每年倾斜1.26毫米,
那么1918-1969这52年间,你
知道比萨斜塔平均每年倾斜
约多少毫米吗?(精确到
0.01毫米).
获取新知
知识点一:加权平均数-权表示重要性
问题:一家公司打算招聘一名英文翻译,对甲、乙两位应试者进行了听、说、读、写、的英语水平测试,他们的各项成绩如表所示:
(1)如果公司想招一名综合能力较强的翻译,请计算两名应试者的平均成绩,应该录用谁?
应试者
听
说
读
写
甲
85
78
85
73
乙
73
80
82
83
(1)如果这家公司想招一名综合能力较强的翻译,计算两名应试者的平均成绩.从他们的成绩看,应该录取谁?
乙的平均成绩为
解:
甲的平均成绩为
,
算术平均数
算术平均数
显然甲的成绩比乙高,所以从成绩看,应该录取甲.
(2)如果这家公司想招一名笔译能力较强的翻译,听、说、读、写成绩按照2︰1︰3︰4的比确定,计算两名应试者的平均成绩.从他们的成绩看,应该录取谁?
解:
,
4
3
1
2
4
3
1
2
权
因为乙的成绩比甲高,所以应该录取乙.
(2)中的各项重要性不同,明显读写要更;
(1)中的各项重要性相同
一般地,若n个数x1,x2,…,xn的权分别是w1,w2,…,wn,则
叫做这n个数的加权平均数.
思考
如果这家公司想招一名口语能力较强的翻译,听、说、读、写成绩按照
3︰3︰2︰2
的比例确定,那么甲、乙两人谁将被录取?与上述问题中的(1)(2)相比较,你能体会到权的作用吗?
权有重要程度的作用.
甲将被录取.
例题讲解
例1
一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分.各项成绩均按百分制计,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:请确定两人的名次.
选手
演讲内容
演讲能力
演讲效果
A
85
95
95
B
95
85
95
解:选手A的最后得分是
选手B的最后得分是
由上可知选手B获得第一名,选手A获得第二名.
权的常见形式:比值或百分数
获取新知
知识点二:加权平均数-权表示频数
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的加权平均数,
其中f1,f2,…,fk分别叫做x1,x2,…,xk的权.
算术平均数与加权平均数的区别和联系
2.在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数,当各项权相等时,计算平均数就要采用算术平均数.
1.算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等);
这里的权,包含了“重要性”或频次两种
探究
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少?
载客量/人
频数(班次)
1≤x<21
3
21
≤x<41
5
41
≤x<61
20
61
≤x<81
22
81
≤x<101
18
101
≤x<121
15
1.数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
载客量/人
组中值
频数(班次)
1≤x<21
11
3
21
≤x<41
31
5
41
≤x<61
51
20
61
≤x<81
71
22
81
≤x<101
91
18
101
≤x<121
111
15
2.根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
解:这天5路公共汽车平均每班的载客量是
例题讲解
例2
某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数).
解:这个跳水队运动员的平均年龄为:
8
16
24
2
≈14(岁).
答:这个跳水队运动员的平均年龄约为14岁.
随堂演练
1.
7名学生的体重(单位:
kg)分别是40,42,43,45,47,47,58,则这组数据的平均数是( )A.44
B.45
C.46
D.47
C
2.
小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( )
A.255分 B.84分
C.84.5分
D.86分
D
3.
从一组数据中取出a个x1,b个x2,c个x3,组成一个样本,那么这个样本的平均数是( )
A.
B.
C.
D.
B
4.
睡眠是评价人类健康水平的一项重要指标,充足的睡眠是青少年健康成长的必要条件之一.小强同学通过问卷调查的方式了解到本班三名同学某天的睡眠时间分别为7.8小时,8.6小时,8.8小时,则这三名同学该天的平均睡眠时间是______小时.
8.4
5.
某班40名学生的某次数学测验成绩统计如下表:
成绩(分)
50
60
70
80
90
100
人数(人)
2
x
10
y
4
2
若这个班该次数学测验的平均成绩是69分,则x=____,y=____.
18
4
6.
某校拟招聘一名优秀数学教师,现有甲、乙、丙三名教师入围,三名教师笔试、面试成绩如下表所示,综合成绩按照笔试占60%、面试占40%进行计算,学校录取综合成绩得分最高者,求被录取教师的综合成绩.
教师
成绩
甲
乙
丙
笔试
80分
82分
78分
面试
76分
74分
78分
解:甲的综合成绩为80×60%+76×40%=78.4(分),
乙的综合成绩为82×60%+74×40%=78.8(分),
丙的综合成绩为78×60%+78×40%=78(分).
因为78<78.4<78.8,
所以被录取的教师为乙,其综合成绩为78.8分.
课堂小结
平均数与加权平均数
加权平均数:
算术平均数:
“重要”型
“频次”型
