2020年秋人教版九年级数学上册24.4 弧长及扇形的面积同步培优(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级数学上册24.4 弧长及扇形的面积同步培优(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 356.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览




文档简介
人教版九年级数学上册《弧长与扇形面积》同步培优
一、选择题
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为(
)
A.5πcm
B.6πcm
C.9πcm
D.8πcm
如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径作半圆,交AB于点D,则阴影部分的面积是( )
A.π﹣1?
??
B.4﹣π??
??
C.???
???
D.2
如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是(
)
A.EF∥CD
B.△COB是等边三角形
C.CG=DG
D.的长为π
如图,正六边形ABCDEF的边长为2,分别以点A,D为圆心,以AB,DC为半径作扇形ABF,扇形DCE.则图中阴影部分的面积是( )
A.6﹣π??
???
B.6﹣π?
???
C.12﹣π??????
D.12﹣π
如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π????
?????
B.2π???
????
C.2π??
????
D.4π
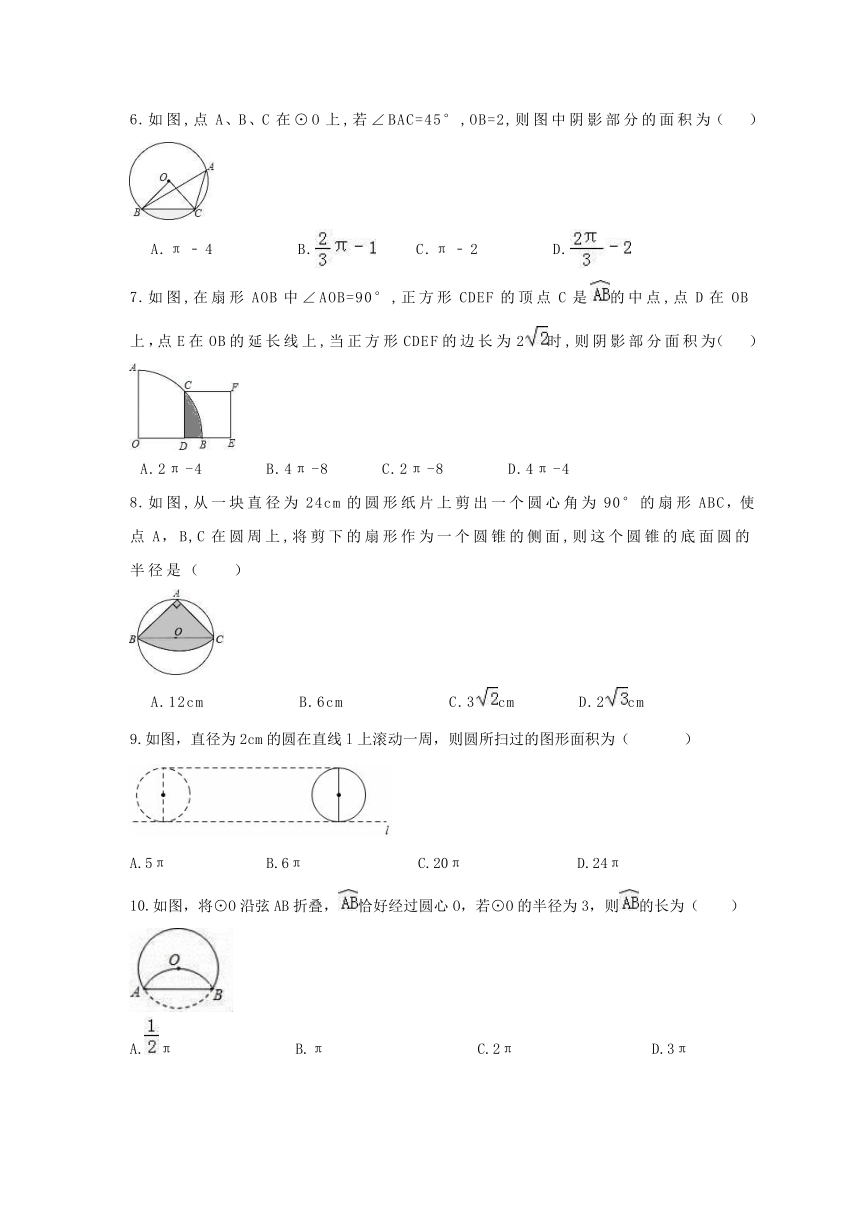
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为(
)
A.π﹣4
B.
C.π﹣2
D.
如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,则阴影部分面积为(
)
A.2π-4
B.4π-8
C.2π-8
D.4π-4
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是(
)
A.12cm
B.6cm
C.3cm
D.2cm
如图,直径为2cm的圆在直线l上滚动一周,则圆所扫过的图形面积为(
)
A.5π???
?
B.6π???
???
C.20π???
???
D.24π
如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为( )
A.π?
??????
B.π????
?????
C.2π????
????
D.3π
如图,在以点O为圆心的半圆中,AB为直径,且AB=4,将该半圆折叠,使点A和点B落在点O处,折痕分别为EC和FD,则图中阴影部分面积为( )
A.4﹣
B.4﹣
C.2﹣
D.2﹣
如图,正方形ABCD的边长为4,将长为4的线段QR的两端放在正方形的相邻的两边上同时滑动.如果Q点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从B点出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为(
)
?
A.16
?
?????
B.????????
C.???
???
D.
二、填空题
扇形的圆心角是80°,半径R=5,则扇形的面积为
一个侧面积为16πcm2的圆锥,其主视图为等腰直角三角形,则这个圆锥高为
cm.
如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为
.
如图,在半径为2
cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为
.
如图,一块等边三角形的木板,边长为1,现将木板沿水平线翻滚,那么B点从开始至结束所走过的路径长度为 .
如图,已知半径为1的⊙O上有三点A、B、C,OC与AB交于点D,∠ADO=85°,∠CAB=20°,则阴影部分的扇形OAC面积是 ??
.
三、解答题
如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
如图,AB为⊙O的直径,C、D是半圆AB的三等分点,过点C作AD延长线的垂线CE,垂足为E.
(1)求证:CE是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
如图,AB为⊙O的直径,BC、AD是⊙O的切线,过O点作EC⊥OD,EC交BC于C,交直线AD于E.
(1)求证:CD是⊙O的切线;
(2)若AE=1,AD=3,求阴影部分的面积.
如图,AB是⊙O的直径,CB,CD分别切⊙O于B,D两点,点E在CD的延长线上,且CE=AE+BC.
(1)求证:AE是⊙O的切线;
(2)若∠C=60°,AB=10,求弧BD的长;
(3)过点D作DF⊥AB于点F,连接BE交DF于点M.求证:DM=MP.
如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求的长(结果保留π).
如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
参考答案
D
答案为:D.
D
B.
B.
C
A
C
A.
C.
D.
C
答案为:50π/9;
答案为:4.
答案为:.
答案为:;
答案为:.
答案为:
.
解:(1)连接OC,∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠BAE,
∴∠OAC=∠CAE,
∴∠OCA=∠CAE,
∴OC∥AE,
∴∠OCD=∠E,
∵AE⊥DE,
∴∠E=90°,
∴∠OCD=90°,
∴OC⊥CD,
∵点C在圆O上,OC为圆O的半径,
∴CD是圆O的切线;
(2)在Rt△AED中,∵∠D=30°,AE=6,
∴AD=2AE=12,
在Rt△OCD中,∵∠D=30°,
∴DO=2OC=DB+OB=DB+OC,
∴DB=OB=OC=AD=4,DO=8,
∴CD===4,
∴S△OCD===8,
∵∠D=30°,∠OCD=90°,
∴∠DOC=60°,
∴S扇形OBC=×π×OC2=,
∵S阴影=S△COD﹣S扇形OBC∴S阴影=8﹣,
∴阴影部分的面积为8﹣.
解:(1)如图所示:△AB′C′即为所求;
(2)∵AB==5,
∴线段AB在变换到AB′的过程中扫过区域的面积为:
=π.
解:
(1)证明:∵点C、D为半圆O的三等分点,
∴,∴∠BOC=∠A,∴OC∥AD,
∵CE⊥AD,∴CE⊥OC,
∴CE为⊙O的切线;
(2)解:连接OD,OC,
∵,∴∠COD=×180°=60°,
∵CD∥AB,
∴S△ACD=S△COD,
∴图中阴影部分的面积=S扇形COD=.
【解答】(1)证明:作OH⊥CD,垂足为H,
∵BC、AD是⊙O的切线,∴∠CBO=∠OAE=90°,
在△BOC和△AOE中,,∴△BOC≌△AOE(ASA),∴OC=OE,
又∵EC⊥OD,∴DE=DC,∴∠ODC=∠ODE,∴OH=OA,∴CD是⊙O的切线;
(2)∵∠E+∠AOE=90°,∠DOA+∠AOE=90°,∴∠E=∠DOA,
又∵∠OAE=∠ODA=90°,∴△AOE∽△ADO,∴=,∴OA2=EA?AD=1×3=3,
∵OA>0,∴OA=,∴tanE==,∴∠DOA=∠E=60°,
∵DA=DH,∠OAD=∠OHD=90°,∴∠DOH=∠DOA=60°,
∴S阴影部分=×3×+×3×﹣=3﹣π.
略
【解答】(1)证明:连接OD,如图所示.
∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.
∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,
∴∠CFD=∠ODF=90°,∴DF⊥AC.
(2)解:∵∠CDF=30°,由(1)得∠ODF=90°,∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.
∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,∴的长===π.
解:(1)PN与⊙O相切.
证明:连接ON,则∠ONA=∠OAN,∵PM=PN,∴∠PNM=∠PMN.
∵∠AMO=∠PMN,∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠OAN=90°.即PN与⊙O相切.
(2)成立.证明:连接ON,则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN.在Rt△AOM中,
∵∠OMA+∠OAM=90°,∴∠PNM+∠ONA=90°.∴∠PNO=180°﹣90°=90°.
即PN与⊙O相切.
(3)解:连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,∴∠PNM=15°,∠OPN=30°,∴∠PON=60°,∠AON=30°.
作NE⊥OD,垂足为点E,则NE=ON?sin60°=1×=.
S阴影=S△AOC+S扇形AON﹣S△CON=OC?OA+CO?NE
=×1×1+π﹣×1×=+π﹣.
一、选择题
如图,AB是⊙O的直径,四边形ABCD内接于⊙O,若BC=CD=DA=4cm,则⊙O的周长为(
)
A.5πcm
B.6πcm
C.9πcm
D.8πcm
如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径作半圆,交AB于点D,则阴影部分的面积是( )
A.π﹣1?
??
B.4﹣π??
??
C.???
???
D.2
如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是(
)
A.EF∥CD
B.△COB是等边三角形
C.CG=DG
D.的长为π
如图,正六边形ABCDEF的边长为2,分别以点A,D为圆心,以AB,DC为半径作扇形ABF,扇形DCE.则图中阴影部分的面积是( )
A.6﹣π??
???
B.6﹣π?
???
C.12﹣π??????
D.12﹣π
如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=4,∠A=45°,则的长度为( )
A.π????
?????
B.2π???
????
C.2π??
????
D.4π
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为(
)
A.π﹣4
B.
C.π﹣2
D.
如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,则阴影部分面积为(
)
A.2π-4
B.4π-8
C.2π-8
D.4π-4
如图,从一块直径为24cm的圆形纸片上剪出一个圆心角为90°的扇形ABC,使点A,B,C在圆周上,将剪下的扇形作为一个圆锥的侧面,则这个圆锥的底面圆的半径是(
)
A.12cm
B.6cm
C.3cm
D.2cm
如图,直径为2cm的圆在直线l上滚动一周,则圆所扫过的图形面积为(
)
A.5π???
?
B.6π???
???
C.20π???
???
D.24π
如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为( )
A.π?
??????
B.π????
?????
C.2π????
????
D.3π
如图,在以点O为圆心的半圆中,AB为直径,且AB=4,将该半圆折叠,使点A和点B落在点O处,折痕分别为EC和FD,则图中阴影部分面积为( )
A.4﹣
B.4﹣
C.2﹣
D.2﹣
如图,正方形ABCD的边长为4,将长为4的线段QR的两端放在正方形的相邻的两边上同时滑动.如果Q点从A点出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从B点出发,沿图中所示方向按B→C→D→A→B滑动到B止,在这个过程中,线段QR的中点M所经过的路线围成的图形的面积为(
)
?
A.16
?
?????
B.????????
C.???
???
D.
二、填空题
扇形的圆心角是80°,半径R=5,则扇形的面积为
一个侧面积为16πcm2的圆锥,其主视图为等腰直角三角形,则这个圆锥高为
cm.
如图,将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置,AB=2,AD=4,则阴影部分的面积为
.
如图,在半径为2
cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为
.
如图,一块等边三角形的木板,边长为1,现将木板沿水平线翻滚,那么B点从开始至结束所走过的路径长度为 .
如图,已知半径为1的⊙O上有三点A、B、C,OC与AB交于点D,∠ADO=85°,∠CAB=20°,则阴影部分的扇形OAC面积是 ??
.
三、解答题
如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB′C′;
(2)计算线段AB在变换到AB′的过程中扫过区域的面积.
如图,AB为⊙O的直径,C、D是半圆AB的三等分点,过点C作AD延长线的垂线CE,垂足为E.
(1)求证:CE是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
如图,AB为⊙O的直径,BC、AD是⊙O的切线,过O点作EC⊥OD,EC交BC于C,交直线AD于E.
(1)求证:CD是⊙O的切线;
(2)若AE=1,AD=3,求阴影部分的面积.
如图,AB是⊙O的直径,CB,CD分别切⊙O于B,D两点,点E在CD的延长线上,且CE=AE+BC.
(1)求证:AE是⊙O的切线;
(2)若∠C=60°,AB=10,求弧BD的长;
(3)过点D作DF⊥AB于点F,连接BE交DF于点M.求证:DM=MP.
如图,在△ABC中,以AB为直径的⊙O分别于BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为5,∠CDF=30°,求的长(结果保留π).
如图,⊙O的半径为1,直线CD经过圆心O,交⊙O于C、D两点,直径AB⊥CD,点M是直线CD上异于点C、O、D的一个动点,AM所在的直线交于⊙O于点N,点P是直线CD上另一点,且PM=PN.
(1)当点M在⊙O内部,如图一,试判断PN与⊙O的关系,并写出证明过程;
(2)当点M在⊙O外部,如图二,其它条件不变时,(1)的结论是否还成立?请说明理由;
(3)当点M在⊙O外部,如图三,∠AMO=15°,求图中阴影部分的面积.
参考答案
D
答案为:D.
D
B.
B.
C
A
C
A.
C.
D.
C
答案为:50π/9;
答案为:4.
答案为:.
答案为:;
答案为:.
答案为:
.
解:(1)连接OC,∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠BAE,
∴∠OAC=∠CAE,
∴∠OCA=∠CAE,
∴OC∥AE,
∴∠OCD=∠E,
∵AE⊥DE,
∴∠E=90°,
∴∠OCD=90°,
∴OC⊥CD,
∵点C在圆O上,OC为圆O的半径,
∴CD是圆O的切线;
(2)在Rt△AED中,∵∠D=30°,AE=6,
∴AD=2AE=12,
在Rt△OCD中,∵∠D=30°,
∴DO=2OC=DB+OB=DB+OC,
∴DB=OB=OC=AD=4,DO=8,
∴CD===4,
∴S△OCD===8,
∵∠D=30°,∠OCD=90°,
∴∠DOC=60°,
∴S扇形OBC=×π×OC2=,
∵S阴影=S△COD﹣S扇形OBC∴S阴影=8﹣,
∴阴影部分的面积为8﹣.
解:(1)如图所示:△AB′C′即为所求;
(2)∵AB==5,
∴线段AB在变换到AB′的过程中扫过区域的面积为:
=π.
解:
(1)证明:∵点C、D为半圆O的三等分点,
∴,∴∠BOC=∠A,∴OC∥AD,
∵CE⊥AD,∴CE⊥OC,
∴CE为⊙O的切线;
(2)解:连接OD,OC,
∵,∴∠COD=×180°=60°,
∵CD∥AB,
∴S△ACD=S△COD,
∴图中阴影部分的面积=S扇形COD=.
【解答】(1)证明:作OH⊥CD,垂足为H,
∵BC、AD是⊙O的切线,∴∠CBO=∠OAE=90°,
在△BOC和△AOE中,,∴△BOC≌△AOE(ASA),∴OC=OE,
又∵EC⊥OD,∴DE=DC,∴∠ODC=∠ODE,∴OH=OA,∴CD是⊙O的切线;
(2)∵∠E+∠AOE=90°,∠DOA+∠AOE=90°,∴∠E=∠DOA,
又∵∠OAE=∠ODA=90°,∴△AOE∽△ADO,∴=,∴OA2=EA?AD=1×3=3,
∵OA>0,∴OA=,∴tanE==,∴∠DOA=∠E=60°,
∵DA=DH,∠OAD=∠OHD=90°,∴∠DOH=∠DOA=60°,
∴S阴影部分=×3×+×3×﹣=3﹣π.
略
【解答】(1)证明:连接OD,如图所示.
∵DF是⊙O的切线,D为切点,∴OD⊥DF,∴∠ODF=90°.
∵BD=CD,OA=OB,∴OD是△ABC的中位线,∴OD∥AC,
∴∠CFD=∠ODF=90°,∴DF⊥AC.
(2)解:∵∠CDF=30°,由(1)得∠ODF=90°,∴∠ODB=180°﹣∠CDF﹣∠ODF=60°.
∵OB=OD,∴△OBD是等边三角形,∴∠BOD=60°,∴的长===π.
解:(1)PN与⊙O相切.
证明:连接ON,则∠ONA=∠OAN,∵PM=PN,∴∠PNM=∠PMN.
∵∠AMO=∠PMN,∴∠PNM=∠AMO.
∴∠PNO=∠PNM+∠ONA=∠AMO+∠OAN=90°.即PN与⊙O相切.
(2)成立.证明:连接ON,则∠ONA=∠OAN,
∵PM=PN,∴∠PNM=∠PMN.在Rt△AOM中,
∵∠OMA+∠OAM=90°,∴∠PNM+∠ONA=90°.∴∠PNO=180°﹣90°=90°.
即PN与⊙O相切.
(3)解:连接ON,由(2)可知∠ONP=90°.
∵∠AMO=15°,PM=PN,∴∠PNM=15°,∠OPN=30°,∴∠PON=60°,∠AON=30°.
作NE⊥OD,垂足为点E,则NE=ON?sin60°=1×=.
S阴影=S△AOC+S扇形AON﹣S△CON=OC?OA+CO?NE
=×1×1+π﹣×1×=+π﹣.
同课章节目录
