华东师大版数学八年级上册-14.1 勾股定理 教案
文档属性
| 名称 | 华东师大版数学八年级上册-14.1 勾股定理 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 877.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 20:16:34 | ||
图片预览

文档简介
14.1
勾股定理
【教学目标】
1.掌握勾股定理的内容;
2.会用勾股定理进行简单计算。
【教学重点】
勾股定理的推导过程
【教学难点】
能对图形性质或数量关系进行猜想及检验。
【教学过程】
一、导入新课:
知识回顾:我们学过直角三角形的哪些性质?
二、自主学习
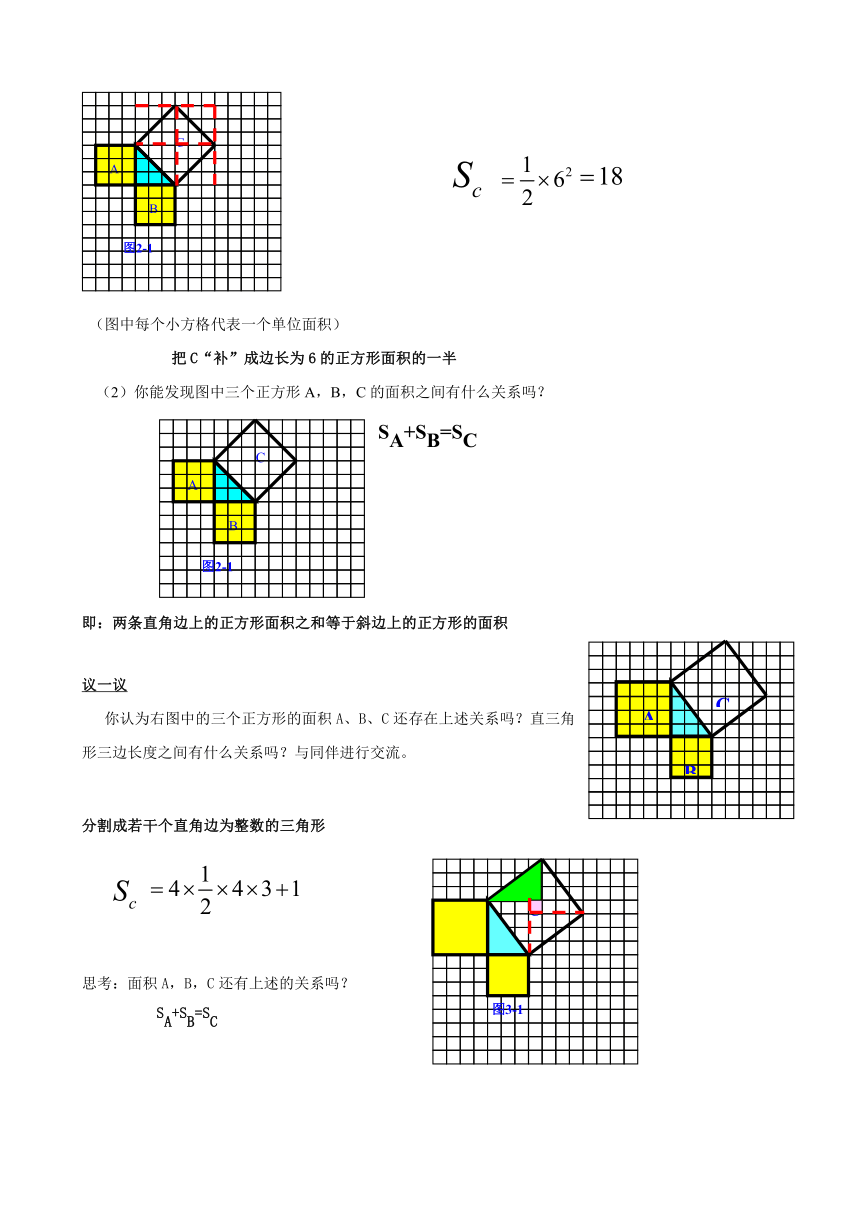
(一)观察左图
正方形A中含有
个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
(图中每个小方格代表一个单位面积)
你是怎样得到上面的结果的?与同伴交流交流。
(图中每个小方格代表一个单位面积)
分“割”成若干个直角边为整数的三角形
(图中每个小方格代表一个单位面积)
把C“补”成边长为6的正方形面积的一半
(2)你能发现图中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
议一议
你认为右图中的三个正方形的面积A、B、C还存在上述关系吗?直三角形三边长度之间有什么关系吗?与同伴进行交流。
分割成若干个直角边为整数的三角形
思考:面积A,B,C还有上述的关系吗?
SA+SB=SC
议一议
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c
之间的关系?
Sa+Sb=Sc
a2+b2=c2
猜想两直角边a、b与斜边c
之间的关系?
勾股定理
直角三角形两直角边的平方和等于斜边的平方.
a2+b2=c2
赵爽弦图
思考:大正方形面积怎么求?
大正方形的面积可以表示为
,又可以表示为
。
所以
结论:
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的。图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就。
图1-1
图1-2
结论变形
直角三角形中,两直角边的平方和等于斜边的平方
c2=a2+b2
a2=c2
-
b2
b2
=c2
-
a2
三、课堂练习
1.求下列直角三角形中未知边的长:
方法小结:
可用勾股定理建立方程。
2.已知Rt△ABC中,∠C=90°。
①若a
=
5,b
=
12,则c=
;
②若c=
10,b
=
8,则a
=
.
③若a=2,c=6,则b=
。
3.若一个直角三角形的三边长分别为3,4,
x,则x=
.
4.如图,一个高3
米,宽4
米的大门,需在相对角的顶点间加一个加固木条,则木条的长为
(
)
A.3
米
B.4
米
C.5米
D.6米
5.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为
(
)
A.50米
B.120米
C.100米
D.130米
附加题:
如图,一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处。折断处离地面的高度是多少?
四、课堂小结:
1、这节课你学到了什么知识?
2、运用“勾股定理”应注意什么问题?
3、你还有什么疑惑或没有弄懂的地方?
五、作业布置:
教材117页1、2题
A
B
C
图2-1
A
B
C
图2-1
A
B
C
图2-1
A
B
C
A
B
C
图3-1
A
B
C
图3-1
42
32
52
A
B
C
a
C
a
b
b
a
b
C
c
5
17
16
x
x
12
8
x
20
3
4
A
B
C
130
120
?
勾股定理
【教学目标】
1.掌握勾股定理的内容;
2.会用勾股定理进行简单计算。
【教学重点】
勾股定理的推导过程
【教学难点】
能对图形性质或数量关系进行猜想及检验。
【教学过程】
一、导入新课:
知识回顾:我们学过直角三角形的哪些性质?
二、自主学习
(一)观察左图
正方形A中含有
个小方格,即A的面积是
个单位面积。
正方形B的面积是
个单位面积。
正方形C的面积是
个单位面积。
(图中每个小方格代表一个单位面积)
你是怎样得到上面的结果的?与同伴交流交流。
(图中每个小方格代表一个单位面积)
分“割”成若干个直角边为整数的三角形
(图中每个小方格代表一个单位面积)
把C“补”成边长为6的正方形面积的一半
(2)你能发现图中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
即:两条直角边上的正方形面积之和等于斜边上的正方形的面积
议一议
你认为右图中的三个正方形的面积A、B、C还存在上述关系吗?直三角形三边长度之间有什么关系吗?与同伴进行交流。
分割成若干个直角边为整数的三角形
思考:面积A,B,C还有上述的关系吗?
SA+SB=SC
议一议
(1)你能用三角形的边长表示正方形的面积吗?
(2)你能发现直角三角形三边长度之间存在什么关系吗?与同伴进行交流。
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c
之间的关系?
Sa+Sb=Sc
a2+b2=c2
猜想两直角边a、b与斜边c
之间的关系?
勾股定理
直角三角形两直角边的平方和等于斜边的平方.
a2+b2=c2
赵爽弦图
思考:大正方形面积怎么求?
大正方形的面积可以表示为
,又可以表示为
。
所以
结论:
读一读
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.图1-1称为“弦图”,最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的。图1-2是在北京召开的2002年国际数学家大会(TCM-2002)的会标,其图案正是“弦图”,它标志着中国古代的数学成就。
图1-1
图1-2
结论变形
直角三角形中,两直角边的平方和等于斜边的平方
c2=a2+b2
a2=c2
-
b2
b2
=c2
-
a2
三、课堂练习
1.求下列直角三角形中未知边的长:
方法小结:
可用勾股定理建立方程。
2.已知Rt△ABC中,∠C=90°。
①若a
=
5,b
=
12,则c=
;
②若c=
10,b
=
8,则a
=
.
③若a=2,c=6,则b=
。
3.若一个直角三角形的三边长分别为3,4,
x,则x=
.
4.如图,一个高3
米,宽4
米的大门,需在相对角的顶点间加一个加固木条,则木条的长为
(
)
A.3
米
B.4
米
C.5米
D.6米
5.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为
(
)
A.50米
B.120米
C.100米
D.130米
附加题:
如图,一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处。折断处离地面的高度是多少?
四、课堂小结:
1、这节课你学到了什么知识?
2、运用“勾股定理”应注意什么问题?
3、你还有什么疑惑或没有弄懂的地方?
五、作业布置:
教材117页1、2题
A
B
C
图2-1
A
B
C
图2-1
A
B
C
图2-1
A
B
C
A
B
C
图3-1
A
B
C
图3-1
42
32
52
A
B
C
a
C
a
b
b
a
b
C
c
5
17
16
x
x
12
8
x
20
3
4
A
B
C
130
120
?
