人教版数学九年级上册 22.1.4二次函数y=ax_+bx+c的图像和性质 教案
文档属性
| 名称 | 人教版数学九年级上册 22.1.4二次函数y=ax_+bx+c的图像和性质 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 59.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 20:18:39 | ||
图片预览

文档简介
二次函数y=ax?+bx+c的图像和性质
教学目标:
知识目标:1、了解二次函数解析式的三种表示方法;
2、抛物线的开口方向、顶点坐标、对称轴以及抛物线与对称轴的交点坐标等;
技能目标:培养学生运用函数知识与几何知识解决数学综合题。
情感目标:1、通过问题情境和探索活动的创设,激发学生的学习兴趣;
2.让学生感受到数学与人类生活的密切联系,体会到学习数学的乐趣。
教学重点:二次函数的图像和性质。
教学难点:二次函数y=
的图像及性质;二次函数的应用。
方法:自主探究、合作交流
教学过程:
一、知识梳理(学生独立练习,分小组批改)
1、二次函数解析式的三种表示方法:
(1)顶点式:
(2)交点式:
(3)一般式:
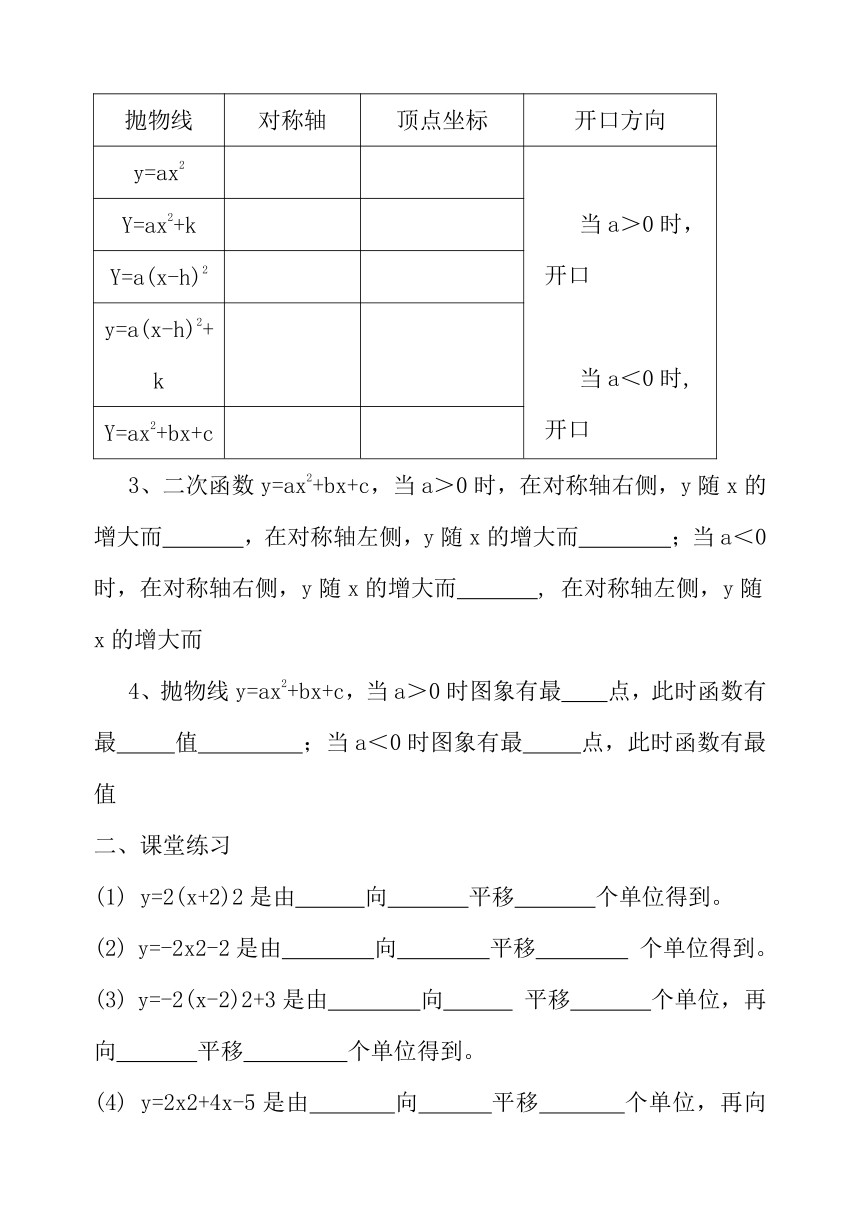
2、填表:
抛物线
对称轴
顶点坐标
开口方向
y=ax2
当a>0时,开口
当a<0时,开口
Y=ax2+k
Y=a(x-h)2
y=a(x-h)2+k
Y=ax2+bx+c
3、二次函数y=ax2+bx+c,当a>0时,在对称轴右侧,y随x的增大而
,在对称轴左侧,y随x的增大而
;当a<0时,在对称轴右侧,y随x的增大而
,
在对称轴左侧,y随x的增大而
4、抛物线y=ax2+bx+c,当a>0时图象有最
点,此时函数有最
值
;当a<0时图象有最
点,此时函数有最
值
二、课堂练习
(1)
y=2(x+2)2是由
向
平移
个单位得到。
(2)
y=-2x2-2是由
向
平移
个单位得到。
(3)
y=-2(x-2)2+3是由
向
平移
个单位,再向
平移
个单位得到。
(4)
y=2x2+4x-5是由
向
平移
个单位,再向
平移
个单位得到。
(5)
y=2x2向左平移2个单位,再向下平移3个单位得到
函数解析式是
。
(6)已知二次函数y=x2-4x-5
,
求下列问题
(7)已知二次函数y=x2+bx+c的顶点坐标(1,-2),求b,c的值
(8)已知二次函数y=x2+4x+c的顶点坐标在x轴上,求c的值
(9)已知二次函数y=x2+4x+c的顶点坐标在直线y=2x+1上,求c的值
2、探究、讨论、练习(先独立思考,再分小组讨论,最后反馈信息)
1、
已知二次函数y=ax2+bx+c的图象如图所示,试判断下面各式的符号:
(1)abc
(2)b2-4ac
(3)2a+b
(4)a+b+c
(上题主要考查学生对二次函数的图象、性质的掌握情况:b2-4ac的符号看抛物线与x轴的交点情况;2a+b看对称轴的位置;而a+b+c的符号要看x=
1时y的值)
(1)已知y=ax2+bx+c的图象如图所示,
a___0,
b____0,
c_____0,
abc____
b2-4ac_____0
a+b+c_____0
a-b+c____0
4a-2b+c___
(2)在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为(
)
(3)已知y=ax2+bx+c的图象如图所示,则下列说法正确的是(
)
A
abc>0
B
a>0,b2-4ac<0
C
当x=1时,函数有最大值为-1
D
当x=1时,函数有最小值为-1
三归纳小结:
提问:通过本节课的练习,你学到了什么知识?
x
y
O
D
y
O
C
x
y
O
B
x
y
O
A
x
y
O
-1
1
教学目标:
知识目标:1、了解二次函数解析式的三种表示方法;
2、抛物线的开口方向、顶点坐标、对称轴以及抛物线与对称轴的交点坐标等;
技能目标:培养学生运用函数知识与几何知识解决数学综合题。
情感目标:1、通过问题情境和探索活动的创设,激发学生的学习兴趣;
2.让学生感受到数学与人类生活的密切联系,体会到学习数学的乐趣。
教学重点:二次函数的图像和性质。
教学难点:二次函数y=
的图像及性质;二次函数的应用。
方法:自主探究、合作交流
教学过程:
一、知识梳理(学生独立练习,分小组批改)
1、二次函数解析式的三种表示方法:
(1)顶点式:
(2)交点式:
(3)一般式:
2、填表:
抛物线
对称轴
顶点坐标
开口方向
y=ax2
当a>0时,开口
当a<0时,开口
Y=ax2+k
Y=a(x-h)2
y=a(x-h)2+k
Y=ax2+bx+c
3、二次函数y=ax2+bx+c,当a>0时,在对称轴右侧,y随x的增大而
,在对称轴左侧,y随x的增大而
;当a<0时,在对称轴右侧,y随x的增大而
,
在对称轴左侧,y随x的增大而
4、抛物线y=ax2+bx+c,当a>0时图象有最
点,此时函数有最
值
;当a<0时图象有最
点,此时函数有最
值
二、课堂练习
(1)
y=2(x+2)2是由
向
平移
个单位得到。
(2)
y=-2x2-2是由
向
平移
个单位得到。
(3)
y=-2(x-2)2+3是由
向
平移
个单位,再向
平移
个单位得到。
(4)
y=2x2+4x-5是由
向
平移
个单位,再向
平移
个单位得到。
(5)
y=2x2向左平移2个单位,再向下平移3个单位得到
函数解析式是
。
(6)已知二次函数y=x2-4x-5
,
求下列问题
(7)已知二次函数y=x2+bx+c的顶点坐标(1,-2),求b,c的值
(8)已知二次函数y=x2+4x+c的顶点坐标在x轴上,求c的值
(9)已知二次函数y=x2+4x+c的顶点坐标在直线y=2x+1上,求c的值
2、探究、讨论、练习(先独立思考,再分小组讨论,最后反馈信息)
1、
已知二次函数y=ax2+bx+c的图象如图所示,试判断下面各式的符号:
(1)abc
(2)b2-4ac
(3)2a+b
(4)a+b+c
(上题主要考查学生对二次函数的图象、性质的掌握情况:b2-4ac的符号看抛物线与x轴的交点情况;2a+b看对称轴的位置;而a+b+c的符号要看x=
1时y的值)
(1)已知y=ax2+bx+c的图象如图所示,
a___0,
b____0,
c_____0,
abc____
b2-4ac_____0
a+b+c_____0
a-b+c____0
4a-2b+c___
(2)在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为(
)
(3)已知y=ax2+bx+c的图象如图所示,则下列说法正确的是(
)
A
abc>0
B
a>0,b2-4ac<0
C
当x=1时,函数有最大值为-1
D
当x=1时,函数有最小值为-1
三归纳小结:
提问:通过本节课的练习,你学到了什么知识?
x
y
O
D
y
O
C
x
y
O
B
x
y
O
A
x
y
O
-1
1
同课章节目录
