北师大版八年级数学下册课件:1.1 第1课时 等腰三角形的性质(26张)
文档属性
| 名称 | 北师大版八年级数学下册课件:1.1 第1课时 等腰三角形的性质(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 257.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
第一章
三角形的证明
1
第1课时
等腰三角形的性质
知识回顾
问题
在八上的“平行线的证明”这一章中,我们学了哪8条基本事实?
1.两点确定一条直线;
2.两点之间线段最短;
3.同一平面内,过一点有且只有一条直线与已知直线垂直;
4.同位角相等,两直线平行;
5.过直线外一点有且只有一条直线与这条直线平行;
6.两边及其夹角分别相等的两个三角形全等;
7.两角及其夹边分别相等的两个三角形全等;
8.三边分别相等的两个三角形全等.
情景导入
问题
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道其中反映了什么数学原理?
获取新知
SSS、SAS、ASA是基本事实,不需要证明,是证明其他定理的基本依据,而AAS不是,需要证明,你能证明AAS吗?
AAS:两角分别相等且其中一组等角的对边相等的两个三角形全等.
你能运用基本事实及已经学过的定理证明上面的推论吗?
知识点一:AAS的证明
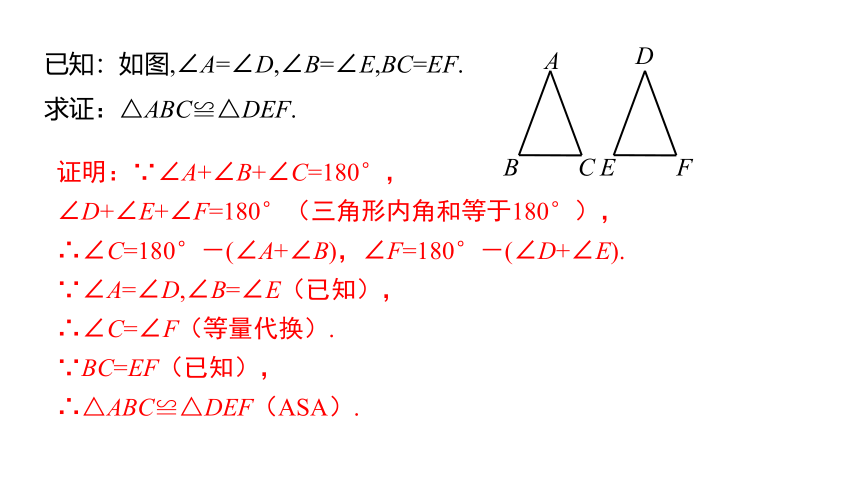
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°),
∴∠C=180°-(∠A+∠B),∠F=180°-(∠D+∠E).
∵∠A=∠D,∠B=∠E(已知),
∴∠C=∠F(等量代换).
∵BC=EF(已知),
∴△ABC≌△DEF(ASA).
F
E
D
C
B
A
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知和求证;
(4)分析证明思路,写出证明过程.
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等(AAS).
根据全等三角形的定义,我们可以得到:
全等三角形的对应边相等,对应角相等.
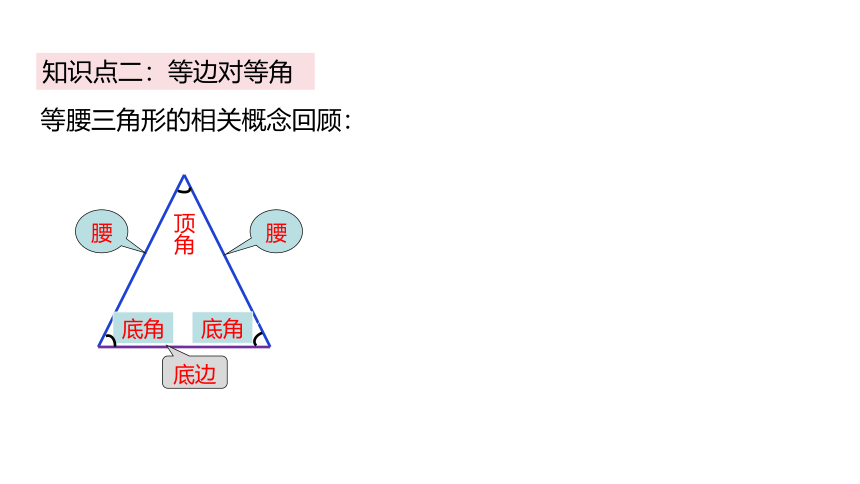
知识点二:等边对等角
等腰三角形的相关概念回顾:
腰
腰
顶角
底角
底角
底边
议一议
(1)还记得我们探索过的等腰三角形的性质吗?
(2)请你选择等腰三角形的一条性质进行证明,并与同伴交流.
定理
等腰三角形的两底角相等.
这一定理可以简述为:等边对等角.
A
C
B
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
我们曾经用折纸的方法说明了等腰三角形的性质。实际上折痕将等腰三角形分成两个全等三家形,这启发我们可以做一条辅助线,把原三角形分成两个全等的三角形
已知:
如图,在△ABC中,AB=AC.
求证:
∠B=
∠C.
证明:作底边的中线AD,则BD=CD.
∴
△BAD≌
△CAD
(SSS).
∴
∠B=
∠C
(全等三角形的对应角相等).
AB=AC
(
已知
),
BD=CD
(
已作
),
AD=AD
(公共边),
在△BAD和△CAD中,
A
B
C
D
方法一:作底边的中线
证明:作顶角的平分线AD,则∠BAD=∠CAD.
AB=AC
(
已知
),
∠BAD=∠CAD
(
已作
),
AD=AD
(公共边),
∴
△BAD
≌
△CAD
(SAS).
∴
∠B=
∠C
(全等三角形的对应角相等).
在△BAD和△CAD中,
A
B
C
D
方法二:作顶角的角平分线
实际上,过顶点作底边上的高也是可以的,这个在学习了后面直角三角形的内容后就能说明了
例题讲解
例1
(1)在△ABC中,AB=AC,若∠A=50°,求∠B;
(2)若等腰三角形的一个角为70°,求顶角的度数;
(3)若等腰三角形的一个角为90°,求顶角的度数.
导引:若给出的条件中底角、顶角不确定,则要分两种情况求解.
解:(1)∵AB=AC,∴∠B=∠C.
∵∠A+∠B+∠C=180°,
∴50°+2∠B=180°,解得∠B=65°.
(3)若顶角为90°,底角为
若底角为90°,则三个内角的和大于180°,不符合三
角形内角和定理.因此顶角为90°.
(2)由题意可知,70°的角可以为顶角或底角,
当底角为70°时,顶角为180°-70°×2=40°.
因此顶角为40°或70°.
获取新知
知识点三:等腰三角形的三线合一
想一想:由△BAD≌
△CAD,除了可以得到∠B=
∠C之外,你还可以得到那些相等的线段和相等的角?和你的同伴交流一下,看看你有什么新的发现?得到什么结论?
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线
.
推论:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
A
C
B
D
1
2
∵AB=AC,
∠1=∠2(已知),
∴BD=CD,AD⊥BC(等腰三角形三线合一).
∵AB=AC,
BD=CD
(已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一).
∵AB=AC,
AD⊥BC(已知),
∴BD=CD,
∠1=∠2(等腰三角形三线合一).
在△ABC中,
例题讲解
例2
如图①,点D、E在△ABC的边BC上,AB=AC.
(1)若AD=AE,求证:BD=CE;
(2)若BD=CE,F为DE的中点,如图②,求证:AF⊥BC.
证明:(1)如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,
∴AF⊥BC.
A
B
D
G
E
C
A
B
D
E
C
F
随堂演练
1.如图,点D,E分别在线段AB,AC上,CD与BE相交于点O,已知AB=AC,现添加以下哪个条件仍不能判定△ABE≌△ACD( )
A.
∠B=∠C
B.
AD=AE
C.
BD=CE
D.
BE=CD
D
2.如图,在等腰三角形ABC中,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
C
3.如图,在△ABC中,AB=AC,D为BC的中点,
∠BAD=35°,则∠C的度数为( )
A.35°
B.45°
C.55°
D.60°
C
4.(1)等腰三角形一个底角为75°,它的另外两个角为___________;
(2)等腰三角形一个角为36°,它的另外两个角为
____________________;
(3)等腰三角形一个角为120°,它的另外两个角为__________.
75°,
30°
72°,72°或36°,108°
30°,30°
5.如图,在△ABC中,AB=AC,AD⊥BC于点D.若AB=6,
CD=4,则△ABC的周长是 .
20
6.如图,在△ABC中
,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x.
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180
°
,
解得x=36
°.
∴∠A=36°,∠ABC=∠C=72°.
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
7.已知:如图,在△ABC中,AB=AC,D为AC上一点,∠DBC=
∠BAC.
求证:BD⊥AC.请你将下面的证明过程补充完整,并在相应的括号内注明理由.
证明:如图,过点A作AE⊥BC于点E,交BD于点F.
∵AB=AC,AE⊥BC,
∴∠CAE=
∠ (
).?
∵∠DBC=∠BAC,
∴∠CAE=∠DBC( ).
∵∠1=∠2,∠ADF=180°-∠2- ,
∠BEF=180°-∠1- ,?
∴∠ADF=∠BEF=90°,
∴BD⊥AC( ).
BAC
等腰三角形的三线合一
等量代换
∠CAE
∠DBC
垂直的定义
课堂小结
等腰三角形的性质
等边对等角
三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上的高和中线与底角的平分线不具有这一性质.
第一章
三角形的证明
1
第1课时
等腰三角形的性质
知识回顾
问题
在八上的“平行线的证明”这一章中,我们学了哪8条基本事实?
1.两点确定一条直线;
2.两点之间线段最短;
3.同一平面内,过一点有且只有一条直线与已知直线垂直;
4.同位角相等,两直线平行;
5.过直线外一点有且只有一条直线与这条直线平行;
6.两边及其夹角分别相等的两个三角形全等;
7.两角及其夹边分别相等的两个三角形全等;
8.三边分别相等的两个三角形全等.
情景导入
问题
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道其中反映了什么数学原理?
获取新知
SSS、SAS、ASA是基本事实,不需要证明,是证明其他定理的基本依据,而AAS不是,需要证明,你能证明AAS吗?
AAS:两角分别相等且其中一组等角的对边相等的两个三角形全等.
你能运用基本事实及已经学过的定理证明上面的推论吗?
知识点一:AAS的证明
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°),
∴∠C=180°-(∠A+∠B),∠F=180°-(∠D+∠E).
∵∠A=∠D,∠B=∠E(已知),
∴∠C=∠F(等量代换).
∵BC=EF(已知),
∴△ABC≌△DEF(ASA).
F
E
D
C
B
A
证明一个命题的一般步骤:
(1)弄清题设和结论;
(2)根据题意画出相应的图形;
(3)根据题设和结论写出已知和求证;
(4)分析证明思路,写出证明过程.
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等(AAS).
根据全等三角形的定义,我们可以得到:
全等三角形的对应边相等,对应角相等.
知识点二:等边对等角
等腰三角形的相关概念回顾:
腰
腰
顶角
底角
底角
底边
议一议
(1)还记得我们探索过的等腰三角形的性质吗?
(2)请你选择等腰三角形的一条性质进行证明,并与同伴交流.
定理
等腰三角形的两底角相等.
这一定理可以简述为:等边对等角.
A
C
B
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
我们曾经用折纸的方法说明了等腰三角形的性质。实际上折痕将等腰三角形分成两个全等三家形,这启发我们可以做一条辅助线,把原三角形分成两个全等的三角形
已知:
如图,在△ABC中,AB=AC.
求证:
∠B=
∠C.
证明:作底边的中线AD,则BD=CD.
∴
△BAD≌
△CAD
(SSS).
∴
∠B=
∠C
(全等三角形的对应角相等).
AB=AC
(
已知
),
BD=CD
(
已作
),
AD=AD
(公共边),
在△BAD和△CAD中,
A
B
C
D
方法一:作底边的中线
证明:作顶角的平分线AD,则∠BAD=∠CAD.
AB=AC
(
已知
),
∠BAD=∠CAD
(
已作
),
AD=AD
(公共边),
∴
△BAD
≌
△CAD
(SAS).
∴
∠B=
∠C
(全等三角形的对应角相等).
在△BAD和△CAD中,
A
B
C
D
方法二:作顶角的角平分线
实际上,过顶点作底边上的高也是可以的,这个在学习了后面直角三角形的内容后就能说明了
例题讲解
例1
(1)在△ABC中,AB=AC,若∠A=50°,求∠B;
(2)若等腰三角形的一个角为70°,求顶角的度数;
(3)若等腰三角形的一个角为90°,求顶角的度数.
导引:若给出的条件中底角、顶角不确定,则要分两种情况求解.
解:(1)∵AB=AC,∴∠B=∠C.
∵∠A+∠B+∠C=180°,
∴50°+2∠B=180°,解得∠B=65°.
(3)若顶角为90°,底角为
若底角为90°,则三个内角的和大于180°,不符合三
角形内角和定理.因此顶角为90°.
(2)由题意可知,70°的角可以为顶角或底角,
当底角为70°时,顶角为180°-70°×2=40°.
因此顶角为40°或70°.
获取新知
知识点三:等腰三角形的三线合一
想一想:由△BAD≌
△CAD,除了可以得到∠B=
∠C之外,你还可以得到那些相等的线段和相等的角?和你的同伴交流一下,看看你有什么新的发现?得到什么结论?
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线
.
推论:等腰三角形顶角的平分线、底边上的中线及底边上的高线互相重合(三线合一).
A
C
B
D
1
2
∵AB=AC,
∠1=∠2(已知),
∴BD=CD,AD⊥BC(等腰三角形三线合一).
∵AB=AC,
BD=CD
(已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一).
∵AB=AC,
AD⊥BC(已知),
∴BD=CD,
∠1=∠2(等腰三角形三线合一).
在△ABC中,
例题讲解
例2
如图①,点D、E在△ABC的边BC上,AB=AC.
(1)若AD=AE,求证:BD=CE;
(2)若BD=CE,F为DE的中点,如图②,求证:AF⊥BC.
证明:(1)如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,
∴AF⊥BC.
A
B
D
G
E
C
A
B
D
E
C
F
随堂演练
1.如图,点D,E分别在线段AB,AC上,CD与BE相交于点O,已知AB=AC,现添加以下哪个条件仍不能判定△ABE≌△ACD( )
A.
∠B=∠C
B.
AD=AE
C.
BD=CE
D.
BE=CD
D
2.如图,在等腰三角形ABC中,AB=AC,若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
A.AE=EC
B.AE=BE
C.∠EBC=∠BAC
D.∠EBC=∠ABE
C
3.如图,在△ABC中,AB=AC,D为BC的中点,
∠BAD=35°,则∠C的度数为( )
A.35°
B.45°
C.55°
D.60°
C
4.(1)等腰三角形一个底角为75°,它的另外两个角为___________;
(2)等腰三角形一个角为36°,它的另外两个角为
____________________;
(3)等腰三角形一个角为120°,它的另外两个角为__________.
75°,
30°
72°,72°或36°,108°
30°,30°
5.如图,在△ABC中,AB=AC,AD⊥BC于点D.若AB=6,
CD=4,则△ABC的周长是 .
20
6.如图,在△ABC中
,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x.
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180
°
,
解得x=36
°.
∴∠A=36°,∠ABC=∠C=72°.
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
7.已知:如图,在△ABC中,AB=AC,D为AC上一点,∠DBC=
∠BAC.
求证:BD⊥AC.请你将下面的证明过程补充完整,并在相应的括号内注明理由.
证明:如图,过点A作AE⊥BC于点E,交BD于点F.
∵AB=AC,AE⊥BC,
∴∠CAE=
∠ (
).?
∵∠DBC=∠BAC,
∴∠CAE=∠DBC( ).
∵∠1=∠2,∠ADF=180°-∠2- ,
∠BEF=180°-∠1- ,?
∴∠ADF=∠BEF=90°,
∴BD⊥AC( ).
BAC
等腰三角形的三线合一
等量代换
∠CAE
∠DBC
垂直的定义
课堂小结
等腰三角形的性质
等边对等角
三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上的高和中线与底角的平分线不具有这一性质.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
