湘教版(2012)初中数学七年级上册 4.2 线段 射线 直线 课件(20张)
文档属性
| 名称 | 湘教版(2012)初中数学七年级上册 4.2 线段 射线 直线 课件(20张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 21:23:49 | ||
图片预览






文档简介
(共20张PPT)
问题1:生活中的线段、射线、直线
插生活射线图片
舞台灯光效果
插生活直线图片
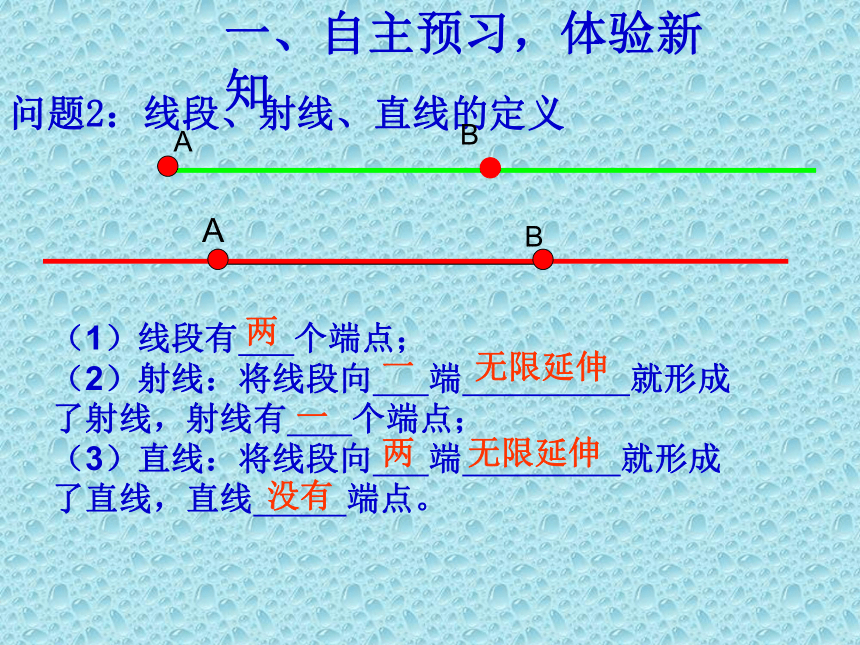
(1)线段有
个端点;
(2)射线:将线段向
端
就形成了射线,射线有
个端点;
(3)直线:将线段向
端
就形成了直线,直线
端点。
问题2:线段、射线、直线的定义
A
B
A
B
两
一
无限延伸
一
两
无限延伸
没有
一、自主预习,体验新知
二、探究实践,感悟新知
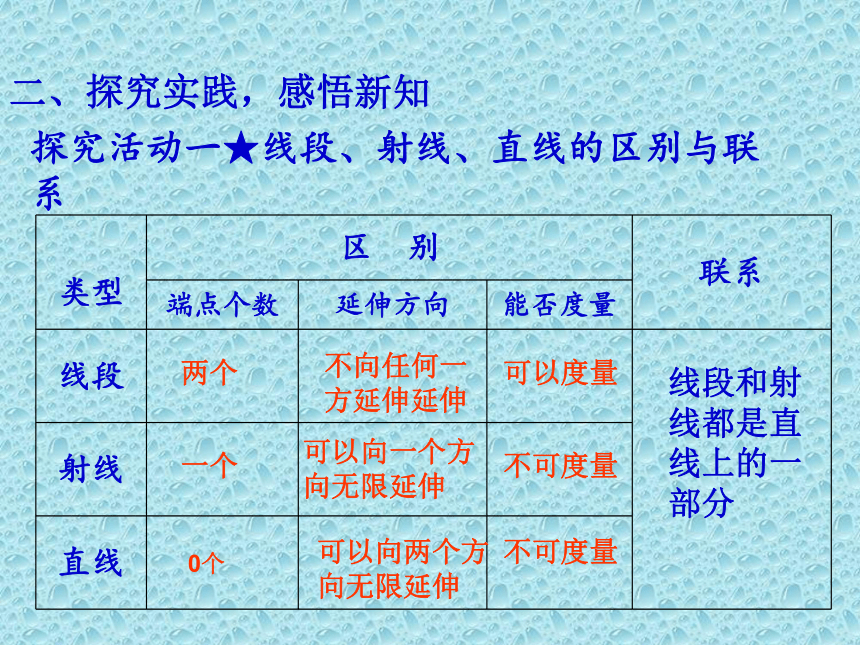
探究活动一★线段、射线、直线的区别与联系
类型
区
别
联系
端点个数
延伸方向
能否度量
线段
射线
直线
两个
0个
一个
不向任何一方延伸延伸
可以度量
可以向一个方向无限延伸
可以向两个方向无限延伸
不可度量
不可度量
线段和射线都是直线上的一部分
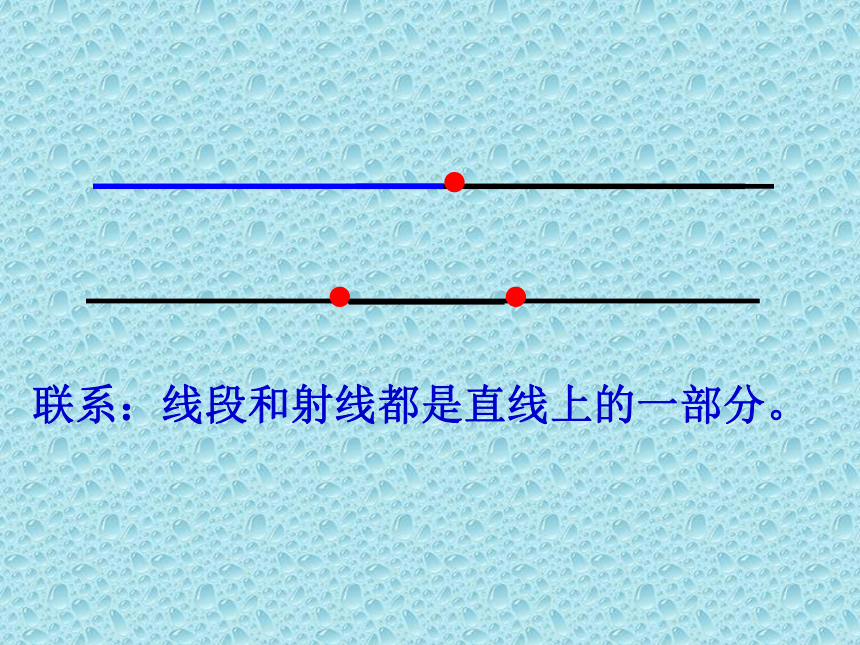
联系:线段和射线都是直线上的一部分。
(2)一条直线长6000千米,一条射线
长3000千米。???????
(???
)
(3)因为射线只能向一端无限延长,
所以射线比直线短。
(???
)
(1)黑板的边是一条射线。?????(???
)
(4)线段是直线的一部分。???
(???
)
×
×
√
×
探究活动二★线段、射线、直线的表示方法
名称
图形
表示方法
注意事项
线段
射线
直线
线段AB或线段BA
线段a
射线AB或射线m
射线BA或射线m
直线AB或直线BA
直线a
用两个端点的字母来表示时,
无先后顺序.
用端点及射线上一点来表示时,注意端点
的字母写在前面.
用直线上两个点来表示时,无先后顺序.
三者表示法的共同点:“两大”或“一小”
M
N
观察图形,判断下列说法是否正确
O
1、直线OM和直线MN是同一条直线(
)
2、射线NM和射线NO是同一条射线(
)
3、射线OM和射线ON是同一条射线(
)
4、射线NO比线段NM短
(
)
√
√
×
×
例:已知点O,P,Q(如图),画线段PQ,射线OP和直线OQ。
O
P
Q
拓展:你能根据下面的语句画图吗?
(2)延长线段PQ至点E;
(1)延长线段QP。
E
延长线一般画成虚线
结论:点和直线有两种位置关系,即点在直线上(或者说直线经过点)和点在直线外(或者说直线不经过点)。
Q
P
B
1、点P在直线m上(或者说直线m经过点P);
2、点Q、B
在直线m外(或者说直线
m不经过点Q、B)。
m
实践活动一:观察点与直线的位置关系
n
m
O
当两条不同的直线只有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点。如图,则称直线m和n相交于点O。
实践活动一:直线和直线的位置关系初探
思考:直线和直线还有其它的位置关系吗?
1.过一点A画一条直线.
请问可以画几条?
·A
过一点A可以画无数条直线
2.过两点A、B可以画几条直线?
请动手试一试.
A
B
实践活动二:
基本事实:
经过两点有且只有一条直线
两点确定一条直线
简述为:
经过一点可以画无数条直线;
经过平面内三点中的任意两点呢?四点呢?
1、过同一平面上的三个点中的任意两个点,可以画几条直线?
(1)
可以画三条直线
(2)
只能画一条直线
2、过同一平面上的四个点中的任意两个点,可以画几条直线?
学以致用
1.将一个细木条固定在墙上,至少需要几个钉子?
2.植树节,同学要把一排树植整齐,怎么办?
只要定出两个树坑的位置就能
确定同一行的树坑所在的直线
挑战乐园
观察下图,思考得到的数字有什么规律?
在线段AB上取1个点C,图中共有
条线段;
在线段AB上取2个点C、D,图中共有
条线段;
在线段AB上取3个点C、D、E,图中共有
条线段.
观察下列规律:
如果在线段AB上取4个点,一共有多少条线段?取5个点呢?n个点呢?
3=1+2;6=1+2+3;10=1+2+3+4
规律:有n个点就有
条线段;
3
6
10
2、(建模)懒羊羊乘火车从邵阳到长沙去参观野生动物园,
它发现往返邵阳、长沙两地的火车中途需要停靠邵东、娄底、
湘乡、湘潭四个站点,那么车站需要制定多少种不同的车票
才能满足在这条线路上往返的不同旅客的需要?
你知道实际生活中还有哪些问题能用类似的方法来解决吗?
本节课知识与能力清单:
(1)★线段、射线、直线的区别与联系;
(2)★线段、射线、直线的表示方法;
(3)★点与直线有两种位置关系;
(4)★(基本事实)过两点
条直线,或者说
两点
一条直线;
(5)★规律:在一条直线上取n个不同的点,可以得
到
条不同的线段;
(6)★学会将不同的几何语言(文字语言、符号语言、
图形
语言)
的相互转化;
(7)★在必要的情况下会用分类讨论的数学思想解决问题。
问题1:生活中的线段、射线、直线
插生活射线图片
舞台灯光效果
插生活直线图片
(1)线段有
个端点;
(2)射线:将线段向
端
就形成了射线,射线有
个端点;
(3)直线:将线段向
端
就形成了直线,直线
端点。
问题2:线段、射线、直线的定义
A
B
A
B
两
一
无限延伸
一
两
无限延伸
没有
一、自主预习,体验新知
二、探究实践,感悟新知
探究活动一★线段、射线、直线的区别与联系
类型
区
别
联系
端点个数
延伸方向
能否度量
线段
射线
直线
两个
0个
一个
不向任何一方延伸延伸
可以度量
可以向一个方向无限延伸
可以向两个方向无限延伸
不可度量
不可度量
线段和射线都是直线上的一部分
联系:线段和射线都是直线上的一部分。
(2)一条直线长6000千米,一条射线
长3000千米。???????
(???
)
(3)因为射线只能向一端无限延长,
所以射线比直线短。
(???
)
(1)黑板的边是一条射线。?????(???
)
(4)线段是直线的一部分。???
(???
)
×
×
√
×
探究活动二★线段、射线、直线的表示方法
名称
图形
表示方法
注意事项
线段
射线
直线
线段AB或线段BA
线段a
射线AB或射线m
射线BA或射线m
直线AB或直线BA
直线a
用两个端点的字母来表示时,
无先后顺序.
用端点及射线上一点来表示时,注意端点
的字母写在前面.
用直线上两个点来表示时,无先后顺序.
三者表示法的共同点:“两大”或“一小”
M
N
观察图形,判断下列说法是否正确
O
1、直线OM和直线MN是同一条直线(
)
2、射线NM和射线NO是同一条射线(
)
3、射线OM和射线ON是同一条射线(
)
4、射线NO比线段NM短
(
)
√
√
×
×
例:已知点O,P,Q(如图),画线段PQ,射线OP和直线OQ。
O
P
Q
拓展:你能根据下面的语句画图吗?
(2)延长线段PQ至点E;
(1)延长线段QP。
E
延长线一般画成虚线
结论:点和直线有两种位置关系,即点在直线上(或者说直线经过点)和点在直线外(或者说直线不经过点)。
Q
P
B
1、点P在直线m上(或者说直线m经过点P);
2、点Q、B
在直线m外(或者说直线
m不经过点Q、B)。
m
实践活动一:观察点与直线的位置关系
n
m
O
当两条不同的直线只有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点。如图,则称直线m和n相交于点O。
实践活动一:直线和直线的位置关系初探
思考:直线和直线还有其它的位置关系吗?
1.过一点A画一条直线.
请问可以画几条?
·A
过一点A可以画无数条直线
2.过两点A、B可以画几条直线?
请动手试一试.
A
B
实践活动二:
基本事实:
经过两点有且只有一条直线
两点确定一条直线
简述为:
经过一点可以画无数条直线;
经过平面内三点中的任意两点呢?四点呢?
1、过同一平面上的三个点中的任意两个点,可以画几条直线?
(1)
可以画三条直线
(2)
只能画一条直线
2、过同一平面上的四个点中的任意两个点,可以画几条直线?
学以致用
1.将一个细木条固定在墙上,至少需要几个钉子?
2.植树节,同学要把一排树植整齐,怎么办?
只要定出两个树坑的位置就能
确定同一行的树坑所在的直线
挑战乐园
观察下图,思考得到的数字有什么规律?
在线段AB上取1个点C,图中共有
条线段;
在线段AB上取2个点C、D,图中共有
条线段;
在线段AB上取3个点C、D、E,图中共有
条线段.
观察下列规律:
如果在线段AB上取4个点,一共有多少条线段?取5个点呢?n个点呢?
3=1+2;6=1+2+3;10=1+2+3+4
规律:有n个点就有
条线段;
3
6
10
2、(建模)懒羊羊乘火车从邵阳到长沙去参观野生动物园,
它发现往返邵阳、长沙两地的火车中途需要停靠邵东、娄底、
湘乡、湘潭四个站点,那么车站需要制定多少种不同的车票
才能满足在这条线路上往返的不同旅客的需要?
你知道实际生活中还有哪些问题能用类似的方法来解决吗?
本节课知识与能力清单:
(1)★线段、射线、直线的区别与联系;
(2)★线段、射线、直线的表示方法;
(3)★点与直线有两种位置关系;
(4)★(基本事实)过两点
条直线,或者说
两点
一条直线;
(5)★规律:在一条直线上取n个不同的点,可以得
到
条不同的线段;
(6)★学会将不同的几何语言(文字语言、符号语言、
图形
语言)
的相互转化;
(7)★在必要的情况下会用分类讨论的数学思想解决问题。
同课章节目录
