第27章 小结与复习 课件(共56张PPT)
文档属性
| 名称 | 第27章 小结与复习 课件(共56张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 14:29:14 | ||
图片预览







文档简介
(共56张PPT)
第二十七章
圆
小结与复习
华东师大版
九年级数学下册
教学课件
要点梳理
1
【知识与技能】
1.掌握圆的相关概念和定理.
2.圆的相关概念和定理的应用.
【过程与方法】
通过对本章知识的系统复习,使学生对本章知识能够全面的了解,掌握.
【情感态度】
在整理知识点的过程中发展学生的独立思考习惯,让学生感受成功,并找到解决圆的相关问题的一般方法.
【教学重点】
掌握圆的相关概念和定理.
【教学难点】
圆的相关概念和定理的应用.
学习目标
要点梳理
·
一、与圆有关的概念
1.圆:平面内到定点的距离等于定长的所有点组成的图形.
2.弦:连结圆上任意两点的线段.
3.直径:经过圆心的弦是圆的直径,直径是最长的弦.
4.劣弧:小于半圆周的圆弧.
5.优弧:大于半圆周的圆弧.
要点梳理
6.等弧:在同圆或等圆中,能够互相重合的弧.
7.圆心角:顶点在圆心,角的两边与圆相交.
8.圆周角:顶点在圆上,角的两边与圆相交.
[注意]
(1)确定圆的要素:圆心决定位置,半径决定大小.(2)不在同一条直线上的三个点确定一个圆.
·
要点梳理
9.外接圆、内接正多边形:将一个圆n(n≥3)等分,依次连接各等分点所得到的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆。
10.三角形的外接圆
外心:三角形的外接圆的圆心叫做这个这个三角形的外心。
[注意]
(1)三角形的外心是三角形三条边的垂直平分线的交点。(2)一个三角形的外接圆是唯一的。
要点梳理
11.三角形的内切圆
内心:三角形的内切圆的圆心叫做这个这个三角形的内心。
[注意]
(1)三角形的内心是三角形三条角平分线的交点。(2)一个三角形的内切圆是唯一的。
要点梳理
12.正多边形的相关概念
(1)中心:正多变形外接圆和内切圆有公共的圆心,称其为正多边形的中心.
(2)半径:外接圆的半径叫做正多边形的半径.
(3)边心距:中心到正多边形一边的距离叫做正多边形的边心距.
(4)中心角:正多边形每一条边对应所对的外接圆的圆心角都相等,叫做正多边形的中心角.
要点梳理
二、与圆有关的位置关系
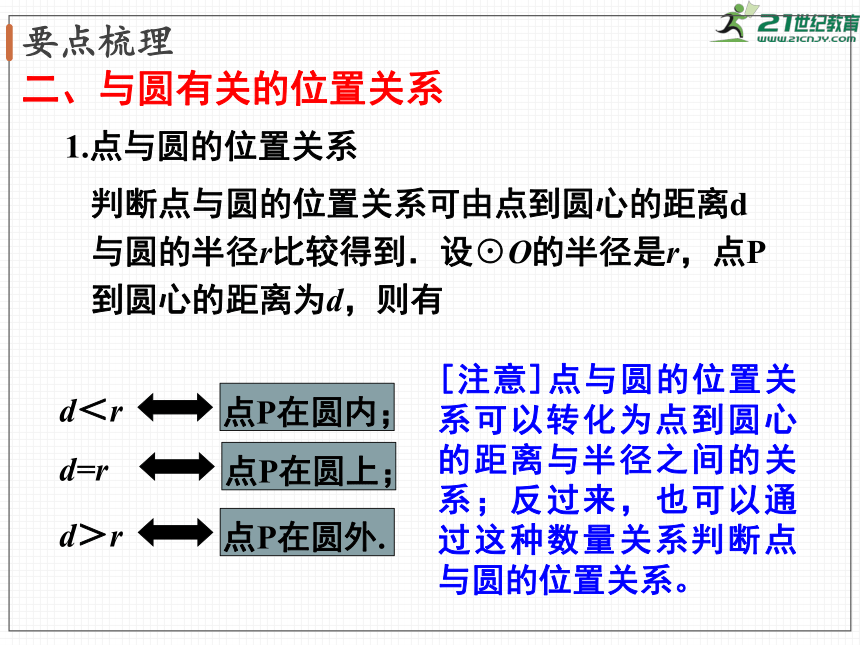
1.点与圆的位置关系
判断点与圆的位置关系可由点到圆心的距离d与圆的半径r比较得到.设☉O的半径是r,点P到圆心的距离为d,则有
点P在圆内;
d<r
点P在圆上;
d=r
点P在圆外.
d>r
[注意]点与圆的位置关系可以转化为点到圆心的距离与半径之间的关系;反过来,也可以通过这种数量关系判断点与圆的位置关系。
要点梳理
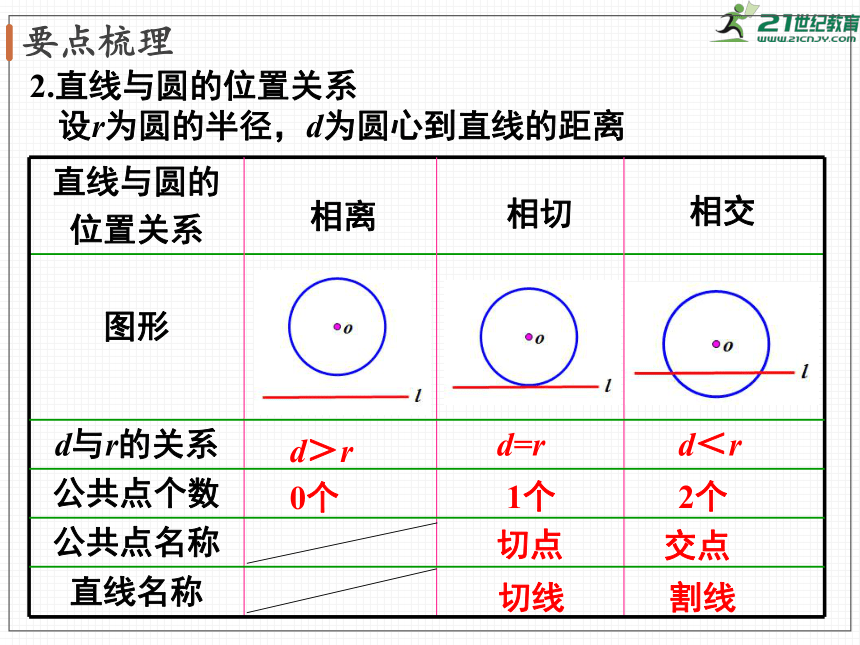
2.直线与圆的位置关系
设r为圆的半径,d为圆心到直线的距离
直线与圆的
位置关系
图形
d与r的关系
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
d>r
d=r
d<r
要点梳理
三、
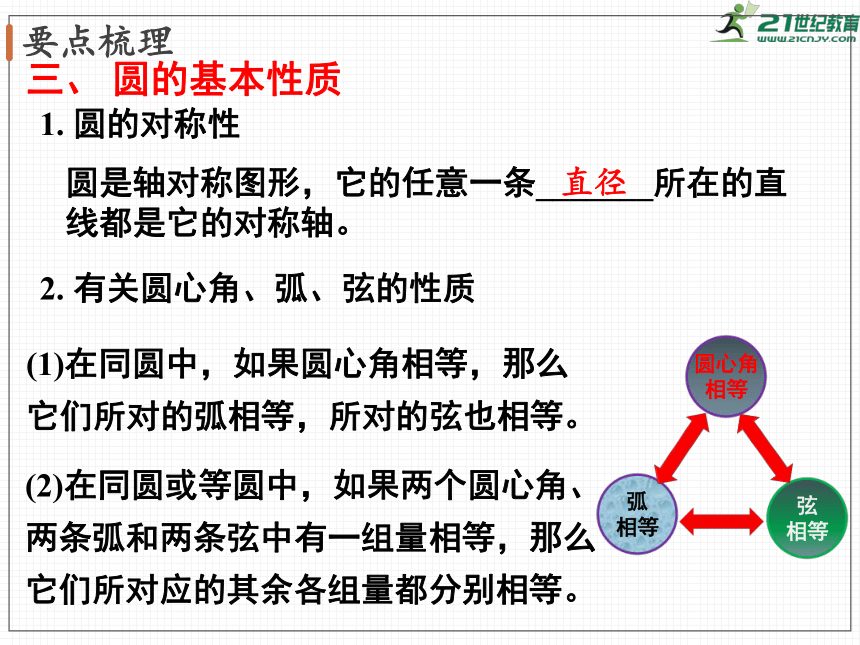
圆的基本性质
1.
圆的对称性
圆是轴对称图形,它的任意一条_______所在的直线都是它的对称轴。
直径
2.
有关圆心角、弧、弦的性质
(1)在同圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等。
(2)在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
圆心角
相等
弧
相等
弦
相等
要点梳理
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;
平分弧的直径垂直平分这条弧所对的弦.
四、有关定理及其推论
1.垂径定理
(1)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的
.
[注意]
①条件中的“弦”可以是直径;②结论中的“平分弧”指平分弦所对的劣弧、优弧.
两条弧
要点梳理
2.圆周角定理
(1)圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
(3)推论2:90°的圆周角所对的弦是直径.
[注意]
“同弧”指“在一个圆中的同一段弧”;“等弧”指“在同圆或等圆中相等的弧”;“同弧或等弧”不能改为“同弦或等弦”.
(4)推论3:圆的内接四边形的对角互补.
(2)推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对弧相等.
要点梳理
3.与切线相关的定理
(1)判定定理:经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
(2)性质定理:圆的切线垂直于经过切点的半径.
(3)切线长定理:经过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
要点梳理
五、圆中的计算问题
1.弧长公式
半径为R的圆中,n°圆心角所对的弧长l=________.
2.扇形面积公式
半径为R,圆心角为n°的扇形面积S=
____________.
或
3.弓形面积公式
O
O
弓形的面积=扇形的面积±三角形的面积
要点梳理
(3)圆锥的侧面积为
.
[注意]
圆锥的侧面展开图的形状是扇形,它的半径等于圆锥的母线长,它的弧长是圆锥底面圆的周长。
(4)圆锥的全面积为
.
4.圆锥的侧面积
(1)圆锥的侧面展开图是一个
.
(2)如果圆锥母线长为l,底面圆的半径为r,那么这个扇形的半径为 ,扇形的弧长为
.
扇形
l
要点梳理
5.圆内接正多边形的计算
(1)正n边形的中心角为
(2)正n边形的边长a,半径R,边心距r之间的关系
(3)边长a,边心距r的正n边形的面积为
其中l为正n边形的周长.
考点讲练
2
考点讲练
核心知识点一
圆周角定理
例1
在图中,BC是☉O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是(
)
A.
72°
B.54°
C.
45°
D.36
°
A
B
C
D
B
考点讲练
135°
1.如图a,四边形ABCD为☉O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是
.
C
D
B
A
P
O
图a
针对训练
考点讲练
2.如图b,线段AB是直径,点D是☉O上一点,
∠CDB=20
°,过点C作☉O的切线交AB的延长线于点E,则∠E等于
.
O
C
A
B
E
D
图b
50°
考点讲练
核心知识点二
垂径定理
例2
工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为
mm.
8mm
A
B
8
C
D
O
解析
设圆心为O,连接AO,作出过点O的弓形高CD,垂足为D,可知AO=5mm,OD=3mm,利用勾股定理进行计算,AD=4mm,所以AB=8mm.
考点讲练
A
O
B
C
E
F
图a
3.如图a,点C是扇形OAB上的AB的任意一点,OA=2,连接AC,BC,过点O作OE
⊥AC,OF
⊥BC,垂足分别为E,F,连接EF,则EF的长度等于
.
(
针对训练
考点讲练
A
B
C
D
P
O
图b
D’
P
4.如图b,AB是⊙O的直径,且AB=2,C,D是同一半圆上的两点,并且AC与BD的度数分别是96
°和36
°,动点P是AB上的任意一点,则PC+PD的最小值是
.
(
(
考点讲练
核心知识点三
与圆有关的位置关系
B
北
60°
30°
A
C
例3
如图,已知灯塔A的周围7海里的范围内有暗礁,一艘鱼轮在B处测得灯塔A在北偏东600的方向,向东航行8海里到达C处后,又测得该灯塔在北偏东300的方向,如果渔轮不改变航向,继续向东航行,有没有触礁的危险?请通过计算说明理由。(参考数据
=1.732)
考点讲练
解析:灯塔A的周围7海里都是暗礁,即表示以A为圆心,7海里为半径的圆中,都是暗礁.渔轮是否会触礁,关键是看渔轮与圆心A之间的距离d的大小关系.
B
北
60°
30°
A
C
考点讲练
B
北
60°
30°
A
C
D
解:如图,作AD垂直于BC于D,根据题意,得BC=8.设AD为x.
∵∠ABC=30°,∴AB=2x.
BD=
x.
∵∠ACD=90°-30°=60°,
∴
AD=CD×tan60°,CD=
.
BC=BD-CD=
=8.
解得
x=
即渔船继续往东行驶,有触礁的危险。
考点讲练
5.
☉O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是(
)
A.点A在☉O内部
B.点A在☉O上
C.点A在☉O外部
D.点A不在☉O上
解析:此题需先计算出一元二次方程x2-6x+8=0的两个根,然后再根据R与d的之间的关系判断出点A与
☉O的关系。
D
针对训练
考点讲练
例4
如图,
O为正方形对角线上一点,以点O
为圆心,OA长为半径的☉O与BC相切于点M.
(1)求证:CD与☉O相切;
A
B
C
D
O
M
(1)证明:过点O作ON⊥CD于N.连接OM
∵BC与☉O相切于点M,
∴
∠OMC=90
°,
∵四边形ABCD是正方形,点O在AC上.
∴AC是∠BCD的角平分线,
∴ON=OM,
∴
CD与☉O相切.
N
考点讲练
A
B
C
D
O
M
(2)解:
∵正方形ABCD的边长为1,AC=
.
设☉O的半径为r,则OC=
.
又易知△OMC是等腰直角三角形,
∴OC=
因此有
,解得
.
(2)若正方形ABCD的边长为1,求☉O的半径.
考点讲练
方法归纳
(1)证切线时添加辅助线的解题方法有两种:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径;有切线时添加辅助线的解题方法是:见切点,连半径,得垂直;
(2)设未知数,通常利用勾股定理建立方程.
考点讲练
6.(多解题)如图,直线AB,CD相交于点O,
∠AOD=30
°,半径为1cm的☉P的圆心在射线OA上,且与点O的距离为6cm,如果☉P以1cm/s的速度沿由A向B的方向移动,那么
秒钟后☉P与直线CD相切.
4或8
解析:
根本题应分为两种情况:(1)☉P在直线AB下面与直线CD相切;(2)☉P在直线AB上面与直线CD相切.
针对训练
A
B
D
C
P
P2
P1
E
考点讲练
例5
已知:如图,PA,PB是⊙O的切线,A、B为切点,过
上的一点C作⊙O的切线,交PA于D,交PB于E.
(1)若∠P=70°,求∠DOE的度数;
解:(1)连接OA、OB、OC,
∵⊙O分别切PA、PB、DE于点A、B、C,∴OA⊥PA,OB⊥PB,OC⊥DE,AD=CD,BE=CE,
∴OD平分∠AOC,OE平分∠BOC.
∴∠DOE=
∠AOB.
∵∠P+∠AOB=180°,∠P=70°,
∴∠DOE=55°.
考点讲练
(2)∵⊙O分别切PA、PB、DE于A、B、C,
∴AD=CD,BE=CE.
∴△PDE的周长=PD+PE+DE
=PD+AD+BE+PE=2PA=8(cm)
(2)若PA=4
cm,求△PDE的周长.
考点讲练
核心知识点四
圆中的计算问题
例6
如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上,
OA=1,∠AOC=120°,∠1=∠2,则扇形OEF的面积?
解:∵四边形OABC为菱形
∴OC=OA=1
∵
∠AOC=120°,∠1=∠2
∴
∠FOE=120°
又∵点C在以点O为圆心的圆上
考点讲练
7.(1)一条弧所对的圆心角为135
°
,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为
.
(2)若一个正六边形的周长为24,则该正六边形的面积为______.
40cm
针对训练
考点讲练
8.如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于_______.
考点讲练
例7
如图所示,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,求图中阴影部分的面积。
考点讲练
解:将线段FC平移到直线AE上,此时点F与点E重合,
点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴
AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在Rt△AC'C中,得
∴正方形ABCD外接圆的半径为
∴正方形ABCD的边长为
考点讲练
当图中出现圆的直径时,一般方法是作出直径所对的圆周角,从而利用“直径所对的圆周角等于
”构造出直角三角形,为进一步利用勾股定理或锐角三角函数提供了条件。
方法总结
考点讲练
9.
如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.
(1)求正方形EFGH的面积;
解:(1)∵正六边形的边长与其半径相等,∴EF=OF=5.
∵四边形EFGH是正方形,
∴FG=EF=5,
∴正方形EFGH的面积是25.
针对训练
考点讲练
(2)∵正六边形的边长与其半径相等,
∴∠OFE=600.
∴正方形的内角是900,
∴∠OFG=∠OFE
+∠EFG=600+900=1500.
由⑴得OF=FG,
∴∠OGF=
(1800-∠OFG)
=
(1800-1500)=150.
(2)连接OF、OG,求∠OGF的度数.
考点讲练
核心知识点五
与圆有关的作图
·
a
b
c
d
a
例8
如何解决“破镜重圆”的问题:
O
·
考点讲练
例9
如何作圆内接正五边形怎么作?
·
O
E
72°
B
A
D
C
(1)用量角器作72°的中心角,得圆的五等分点;
(2)依次连接各等分点,得圆的内接正五边形。
考点讲练
核心知识点六
圆的综合
[解析]
连接BD,则在Rt△BCD中,BE=DE,利用角的互余证明∠C=∠EDC.
例10
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,过点D的切线交BC于E.
(1)求证:BC=2DE.
考点讲练
解:(1)证明:连接BD,
∵AB为直径,∠ABC=90°,
∴BE切☉O于点B.
又∵DE切☉O于点D,∴DE=BE,
∴∠EBD=∠EDB.
∵∠ADB=90°,
∴∠EBD+∠C=90°,∠BDE+∠CDE=90°.
∴∠C=∠CDE,DE=CE.
∴BC=BE+CE=2DE.
考点讲练
(2)∵DE=2,∴BC=2DE=4.
在Rt△ABC中,
∴AB=BC?
=
在Rt△ABC中,
又∵△ABD∽△ACB,
∴
即
∴
(2)若tanC=
,DE=2,求AD的长.
考点讲练
10.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,连接BD.
针对训练
考点讲练
解:(1)∵AB是直径,∴∠ADB=90°.
∵AD=3,BD=4,∴AB=5.
∵∠CDB=∠ABC,∠A=∠A,
∴△ADB∽△ABC,
∵
即
∴BC=
(1)若AD=3,BD=4,求边BC的长.
考点讲练
又∵∠OBD+∠DBC=90°,∠C+∠D=90°,
∴∠C=∠OBD,∴∠BDO=∠CDE.
∵AB是直径,∴∠ADB=90°,
∴∠BDC=90°,
即∠BDE+∠CDE=90°.
∴∠BDE+∠BDO=90°,即∠ODE=90°.
∴ED与☉O相切.
(2)证明:连接OD,在Rt△BDC中,
∵E是BC的中点,∴CE=DE,∴∠C=∠CDE.
又OD=OB,∴∠ODB=∠OBD.
(2)取BC的中点E,连接ED,试证明ED与☉O相切.
知识小结
3
知识小结
圆
圆的性质
与圆有关的位置关系
弧长与扇形面积的计算
圆的对称性
圆是中心对称图形
垂径定理
四边形的内接圆、三角形的外接圆
直线与圆的位置的关系
切线长定理
圆的概念
圆心角、圆周角、弧与弦之间的关系
圆是轴对称图形,任意一条直径所在直线都是它的对称轴
切线
三角形的内切圆
正多边形与圆
作图
课后作业
4
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第二十七章
圆
小结与复习
华东师大版
九年级数学下册
教学课件
要点梳理
1
【知识与技能】
1.掌握圆的相关概念和定理.
2.圆的相关概念和定理的应用.
【过程与方法】
通过对本章知识的系统复习,使学生对本章知识能够全面的了解,掌握.
【情感态度】
在整理知识点的过程中发展学生的独立思考习惯,让学生感受成功,并找到解决圆的相关问题的一般方法.
【教学重点】
掌握圆的相关概念和定理.
【教学难点】
圆的相关概念和定理的应用.
学习目标
要点梳理
·
一、与圆有关的概念
1.圆:平面内到定点的距离等于定长的所有点组成的图形.
2.弦:连结圆上任意两点的线段.
3.直径:经过圆心的弦是圆的直径,直径是最长的弦.
4.劣弧:小于半圆周的圆弧.
5.优弧:大于半圆周的圆弧.
要点梳理
6.等弧:在同圆或等圆中,能够互相重合的弧.
7.圆心角:顶点在圆心,角的两边与圆相交.
8.圆周角:顶点在圆上,角的两边与圆相交.
[注意]
(1)确定圆的要素:圆心决定位置,半径决定大小.(2)不在同一条直线上的三个点确定一个圆.
·
要点梳理
9.外接圆、内接正多边形:将一个圆n(n≥3)等分,依次连接各等分点所得到的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆。
10.三角形的外接圆
外心:三角形的外接圆的圆心叫做这个这个三角形的外心。
[注意]
(1)三角形的外心是三角形三条边的垂直平分线的交点。(2)一个三角形的外接圆是唯一的。
要点梳理
11.三角形的内切圆
内心:三角形的内切圆的圆心叫做这个这个三角形的内心。
[注意]
(1)三角形的内心是三角形三条角平分线的交点。(2)一个三角形的内切圆是唯一的。
要点梳理
12.正多边形的相关概念
(1)中心:正多变形外接圆和内切圆有公共的圆心,称其为正多边形的中心.
(2)半径:外接圆的半径叫做正多边形的半径.
(3)边心距:中心到正多边形一边的距离叫做正多边形的边心距.
(4)中心角:正多边形每一条边对应所对的外接圆的圆心角都相等,叫做正多边形的中心角.
要点梳理
二、与圆有关的位置关系
1.点与圆的位置关系
判断点与圆的位置关系可由点到圆心的距离d与圆的半径r比较得到.设☉O的半径是r,点P到圆心的距离为d,则有
点P在圆内;
d<r
点P在圆上;
d=r
点P在圆外.
d>r
[注意]点与圆的位置关系可以转化为点到圆心的距离与半径之间的关系;反过来,也可以通过这种数量关系判断点与圆的位置关系。
要点梳理
2.直线与圆的位置关系
设r为圆的半径,d为圆心到直线的距离
直线与圆的
位置关系
图形
d与r的关系
公共点个数
公共点名称
直线名称
2个
交点
割线
1个
切点
切线
0个
相离
相切
相交
d>r
d=r
d<r
要点梳理
三、
圆的基本性质
1.
圆的对称性
圆是轴对称图形,它的任意一条_______所在的直线都是它的对称轴。
直径
2.
有关圆心角、弧、弦的性质
(1)在同圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等。
(2)在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
圆心角
相等
弧
相等
弦
相等
要点梳理
(2)垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧;
平分弧的直径垂直平分这条弧所对的弦.
四、有关定理及其推论
1.垂径定理
(1)垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的
.
[注意]
①条件中的“弦”可以是直径;②结论中的“平分弧”指平分弦所对的劣弧、优弧.
两条弧
要点梳理
2.圆周角定理
(1)圆周角定理:圆周角的度数等于它所对弧上的圆心角度数的一半.
(3)推论2:90°的圆周角所对的弦是直径.
[注意]
“同弧”指“在一个圆中的同一段弧”;“等弧”指“在同圆或等圆中相等的弧”;“同弧或等弧”不能改为“同弦或等弦”.
(4)推论3:圆的内接四边形的对角互补.
(2)推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对弧相等.
要点梳理
3.与切线相关的定理
(1)判定定理:经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
(2)性质定理:圆的切线垂直于经过切点的半径.
(3)切线长定理:经过圆外一点所画的圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
要点梳理
五、圆中的计算问题
1.弧长公式
半径为R的圆中,n°圆心角所对的弧长l=________.
2.扇形面积公式
半径为R,圆心角为n°的扇形面积S=
____________.
或
3.弓形面积公式
O
O
弓形的面积=扇形的面积±三角形的面积
要点梳理
(3)圆锥的侧面积为
.
[注意]
圆锥的侧面展开图的形状是扇形,它的半径等于圆锥的母线长,它的弧长是圆锥底面圆的周长。
(4)圆锥的全面积为
.
4.圆锥的侧面积
(1)圆锥的侧面展开图是一个
.
(2)如果圆锥母线长为l,底面圆的半径为r,那么这个扇形的半径为 ,扇形的弧长为
.
扇形
l
要点梳理
5.圆内接正多边形的计算
(1)正n边形的中心角为
(2)正n边形的边长a,半径R,边心距r之间的关系
(3)边长a,边心距r的正n边形的面积为
其中l为正n边形的周长.
考点讲练
2
考点讲练
核心知识点一
圆周角定理
例1
在图中,BC是☉O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是(
)
A.
72°
B.54°
C.
45°
D.36
°
A
B
C
D
B
考点讲练
135°
1.如图a,四边形ABCD为☉O的内接正方形,点P为劣弧BC上的任意一点(不与B,C重合),则∠BPC的度数是
.
C
D
B
A
P
O
图a
针对训练
考点讲练
2.如图b,线段AB是直径,点D是☉O上一点,
∠CDB=20
°,过点C作☉O的切线交AB的延长线于点E,则∠E等于
.
O
C
A
B
E
D
图b
50°
考点讲练
核心知识点二
垂径定理
例2
工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为
mm.
8mm
A
B
8
C
D
O
解析
设圆心为O,连接AO,作出过点O的弓形高CD,垂足为D,可知AO=5mm,OD=3mm,利用勾股定理进行计算,AD=4mm,所以AB=8mm.
考点讲练
A
O
B
C
E
F
图a
3.如图a,点C是扇形OAB上的AB的任意一点,OA=2,连接AC,BC,过点O作OE
⊥AC,OF
⊥BC,垂足分别为E,F,连接EF,则EF的长度等于
.
(
针对训练
考点讲练
A
B
C
D
P
O
图b
D’
P
4.如图b,AB是⊙O的直径,且AB=2,C,D是同一半圆上的两点,并且AC与BD的度数分别是96
°和36
°,动点P是AB上的任意一点,则PC+PD的最小值是
.
(
(
考点讲练
核心知识点三
与圆有关的位置关系
B
北
60°
30°
A
C
例3
如图,已知灯塔A的周围7海里的范围内有暗礁,一艘鱼轮在B处测得灯塔A在北偏东600的方向,向东航行8海里到达C处后,又测得该灯塔在北偏东300的方向,如果渔轮不改变航向,继续向东航行,有没有触礁的危险?请通过计算说明理由。(参考数据
=1.732)
考点讲练
解析:灯塔A的周围7海里都是暗礁,即表示以A为圆心,7海里为半径的圆中,都是暗礁.渔轮是否会触礁,关键是看渔轮与圆心A之间的距离d的大小关系.
B
北
60°
30°
A
C
考点讲练
B
北
60°
30°
A
C
D
解:如图,作AD垂直于BC于D,根据题意,得BC=8.设AD为x.
∵∠ABC=30°,∴AB=2x.
BD=
x.
∵∠ACD=90°-30°=60°,
∴
AD=CD×tan60°,CD=
.
BC=BD-CD=
=8.
解得
x=
即渔船继续往东行驶,有触礁的危险。
考点讲练
5.
☉O的半径为R,圆心到点A的距离为d,且R、d分别是方程x2-6x+8=0的两根,则点A与☉O的位置关系是(
)
A.点A在☉O内部
B.点A在☉O上
C.点A在☉O外部
D.点A不在☉O上
解析:此题需先计算出一元二次方程x2-6x+8=0的两个根,然后再根据R与d的之间的关系判断出点A与
☉O的关系。
D
针对训练
考点讲练
例4
如图,
O为正方形对角线上一点,以点O
为圆心,OA长为半径的☉O与BC相切于点M.
(1)求证:CD与☉O相切;
A
B
C
D
O
M
(1)证明:过点O作ON⊥CD于N.连接OM
∵BC与☉O相切于点M,
∴
∠OMC=90
°,
∵四边形ABCD是正方形,点O在AC上.
∴AC是∠BCD的角平分线,
∴ON=OM,
∴
CD与☉O相切.
N
考点讲练
A
B
C
D
O
M
(2)解:
∵正方形ABCD的边长为1,AC=
.
设☉O的半径为r,则OC=
.
又易知△OMC是等腰直角三角形,
∴OC=
因此有
,解得
.
(2)若正方形ABCD的边长为1,求☉O的半径.
考点讲练
方法归纳
(1)证切线时添加辅助线的解题方法有两种:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径;有切线时添加辅助线的解题方法是:见切点,连半径,得垂直;
(2)设未知数,通常利用勾股定理建立方程.
考点讲练
6.(多解题)如图,直线AB,CD相交于点O,
∠AOD=30
°,半径为1cm的☉P的圆心在射线OA上,且与点O的距离为6cm,如果☉P以1cm/s的速度沿由A向B的方向移动,那么
秒钟后☉P与直线CD相切.
4或8
解析:
根本题应分为两种情况:(1)☉P在直线AB下面与直线CD相切;(2)☉P在直线AB上面与直线CD相切.
针对训练
A
B
D
C
P
P2
P1
E
考点讲练
例5
已知:如图,PA,PB是⊙O的切线,A、B为切点,过
上的一点C作⊙O的切线,交PA于D,交PB于E.
(1)若∠P=70°,求∠DOE的度数;
解:(1)连接OA、OB、OC,
∵⊙O分别切PA、PB、DE于点A、B、C,∴OA⊥PA,OB⊥PB,OC⊥DE,AD=CD,BE=CE,
∴OD平分∠AOC,OE平分∠BOC.
∴∠DOE=
∠AOB.
∵∠P+∠AOB=180°,∠P=70°,
∴∠DOE=55°.
考点讲练
(2)∵⊙O分别切PA、PB、DE于A、B、C,
∴AD=CD,BE=CE.
∴△PDE的周长=PD+PE+DE
=PD+AD+BE+PE=2PA=8(cm)
(2)若PA=4
cm,求△PDE的周长.
考点讲练
核心知识点四
圆中的计算问题
例6
如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上,
OA=1,∠AOC=120°,∠1=∠2,则扇形OEF的面积?
解:∵四边形OABC为菱形
∴OC=OA=1
∵
∠AOC=120°,∠1=∠2
∴
∠FOE=120°
又∵点C在以点O为圆心的圆上
考点讲练
7.(1)一条弧所对的圆心角为135
°
,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为
.
(2)若一个正六边形的周长为24,则该正六边形的面积为______.
40cm
针对训练
考点讲练
8.如图,已知C,D是以AB为直径的半圆周上的两点,O是圆心,半径OA=2,∠COD=120°,则图中阴影部分的面积等于_______.
考点讲练
例7
如图所示,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,求图中阴影部分的面积。
考点讲练
解:将线段FC平移到直线AE上,此时点F与点E重合,
点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴
AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在Rt△AC'C中,得
∴正方形ABCD外接圆的半径为
∴正方形ABCD的边长为
考点讲练
当图中出现圆的直径时,一般方法是作出直径所对的圆周角,从而利用“直径所对的圆周角等于
”构造出直角三角形,为进一步利用勾股定理或锐角三角函数提供了条件。
方法总结
考点讲练
9.
如图,正六边形ABCDEF内接于半径为5的⊙O,四边形EFGH是正方形.
(1)求正方形EFGH的面积;
解:(1)∵正六边形的边长与其半径相等,∴EF=OF=5.
∵四边形EFGH是正方形,
∴FG=EF=5,
∴正方形EFGH的面积是25.
针对训练
考点讲练
(2)∵正六边形的边长与其半径相等,
∴∠OFE=600.
∴正方形的内角是900,
∴∠OFG=∠OFE
+∠EFG=600+900=1500.
由⑴得OF=FG,
∴∠OGF=
(1800-∠OFG)
=
(1800-1500)=150.
(2)连接OF、OG,求∠OGF的度数.
考点讲练
核心知识点五
与圆有关的作图
·
a
b
c
d
a
例8
如何解决“破镜重圆”的问题:
O
·
考点讲练
例9
如何作圆内接正五边形怎么作?
·
O
E
72°
B
A
D
C
(1)用量角器作72°的中心角,得圆的五等分点;
(2)依次连接各等分点,得圆的内接正五边形。
考点讲练
核心知识点六
圆的综合
[解析]
连接BD,则在Rt△BCD中,BE=DE,利用角的互余证明∠C=∠EDC.
例10
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,过点D的切线交BC于E.
(1)求证:BC=2DE.
考点讲练
解:(1)证明:连接BD,
∵AB为直径,∠ABC=90°,
∴BE切☉O于点B.
又∵DE切☉O于点D,∴DE=BE,
∴∠EBD=∠EDB.
∵∠ADB=90°,
∴∠EBD+∠C=90°,∠BDE+∠CDE=90°.
∴∠C=∠CDE,DE=CE.
∴BC=BE+CE=2DE.
考点讲练
(2)∵DE=2,∴BC=2DE=4.
在Rt△ABC中,
∴AB=BC?
=
在Rt△ABC中,
又∵△ABD∽△ACB,
∴
即
∴
(2)若tanC=
,DE=2,求AD的长.
考点讲练
10.
如图,在Rt△ABC中,∠ABC=90°,以AB为直径的☉O交AC于点D,连接BD.
针对训练
考点讲练
解:(1)∵AB是直径,∴∠ADB=90°.
∵AD=3,BD=4,∴AB=5.
∵∠CDB=∠ABC,∠A=∠A,
∴△ADB∽△ABC,
∵
即
∴BC=
(1)若AD=3,BD=4,求边BC的长.
考点讲练
又∵∠OBD+∠DBC=90°,∠C+∠D=90°,
∴∠C=∠OBD,∴∠BDO=∠CDE.
∵AB是直径,∴∠ADB=90°,
∴∠BDC=90°,
即∠BDE+∠CDE=90°.
∴∠BDE+∠BDO=90°,即∠ODE=90°.
∴ED与☉O相切.
(2)证明:连接OD,在Rt△BDC中,
∵E是BC的中点,∴CE=DE,∴∠C=∠CDE.
又OD=OB,∴∠ODB=∠OBD.
(2)取BC的中点E,连接ED,试证明ED与☉O相切.
知识小结
3
知识小结
圆
圆的性质
与圆有关的位置关系
弧长与扇形面积的计算
圆的对称性
圆是中心对称图形
垂径定理
四边形的内接圆、三角形的外接圆
直线与圆的位置的关系
切线长定理
圆的概念
圆心角、圆周角、弧与弦之间的关系
圆是轴对称图形,任意一条直径所在直线都是它的对称轴
切线
三角形的内切圆
正多边形与圆
作图
课后作业
4
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
