苏科版数学八年级上册 4.3 实数复习 课件(24张)
文档属性
| 名称 | 苏科版数学八年级上册 4.3 实数复习 课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 363.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
第四章:实数复习
苏科版
一、概念复方根,算术平方根,
被开方数,根指数,
开平方,开立方,
无理数,实数
正数a的正的平方根也叫做a的算术平方根,
求一个数的平方根(立方根)的运算,叫做开平方(开立方)
。
一般地,如果一个数的平方等于a
,这个数叫做a的平方根。(也叫二次方根)
平方根、算术平方根、立方根的定义
数
的立方根用符号
表示。
一般地,如果
,那么
叫
的立方根
区别
你知道算术平方根、平方根、立方根的区别吗?
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(1个)
0
没有
互为相反数(2个)
0
没有
正数(1个)
0
负数(一个)
求一个数的平方根的运算叫开平方
求一个数的立方根的运算叫开立方
≠
是本身
0,1
0
0,1,-1
1.填一填
25的平方根是
;16的算术平方根是
;
27的立方根是
;
的平方根是
,
4
3
针对练习一——平方根
立方根
8
-0.4
0.3
±5
±2
针对练习一——平方根
立方根
2.火眼晴晴选一选
(1)下列说法中正确的是(
)
A.
的平方根是±3
B.1的立方根是±1
C.
=±1
D.
是5的平方根的相反数
(2)下列说法中
①
-4是16的算术平方根
②4是16的算术平方根
③-7是49的算术平方根
④7是(-7)?的算术平方根
其中正确的是(
)
A.
①③
B.
②③
C.
②④
D.
①④
A
C
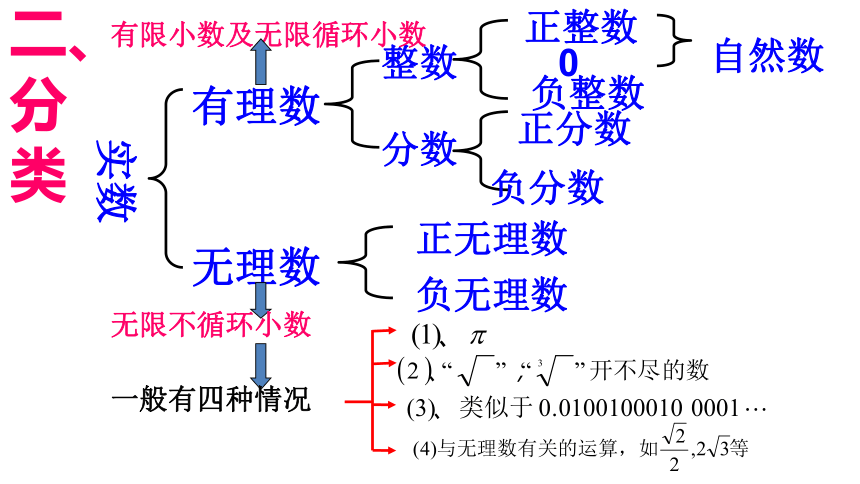
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有四种情况
二、分类
针对练习二——实数分类
中无理数的个
A.
2
B.
3
C.
4
D.
5
B
1、在下列各数
数是(
)个
2.
下列说法错误的有(
)个
①无限小数一定是无理数;
②无理数一定是无限小数;
③带根号的数一定是无理数;
④不带根号的数一定是有理数.
A.
1
B.2
C.3
D.4
C
针对练习二——实数分类
无理数集合:
有理数集合:
整数集合:
分数集合:
3.将下列各数分别填入下列的集合括号中
针对练习二——实数分类
1.实数与数轴:实数与数轴上的点__________对应。
2.实数的相反数、绝对值:
相反数:实数a的相反数为______;
绝对值:正数的绝对值是它的本身;负数的绝对值是它的相反数;零的绝对值是零.即实数的绝对值是非负数。
三、实数的相关概念及运算
实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则与运算律对实数仍然适用。
0
一一
的相反数是
;
相反数是
;
;
。
2.
3.如图,以数轴的单位长线段为边做一个正方形,以数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是(
)
A.1.5
B.1.4
C.
D.
C
针对练习三——实数相关概念、运算
-3
1
0
针对练习三——实数相关概念、运算
4.
5.计算
6.求
的值:
方法:(1)利用数轴:在数轴上表示的两个
实数,
。
正数
零
负数。
(2)利用绝对值:
两个负数比较,
。
(3)平方法
(4)分母(子)有理化
(四)实数大小比较
大于
大于
绝对值大的反而小
右边的数总比左边的数大
2.实数
在数轴上的对应点如图所示,
则它们从小到大的顺序是
。
c
d
0
b
针对练习四——实数大小比较
1.下列各数中,最小的数是
(
)
A.-1
B.0
C.1
D.-
D
3.比较下列各组数的大小
知识拓展
掌握规律
注意平方根和立方根的移位法则
五、扩大,缩小
11.8
0.3535
74500
针对练习五——扩大和缩小
3280
328000
1.π的整数部分为3,则它的小数部分是
;
π-3
2
六、无理数的整数部分与小数部分
七、式子有意义
1、在开平方运算中,被开方数具有非负性
2、分母不为0
针对练习七——有意义的条件
7、式子有意义的条件
1、平方根立方根有关概念
2、实数分类
3、实数有关运算
5、扩大、缩小的变化规律
4、实数大小比较
6、明确表示一个数的小数部分和整数部分
总结
谢谢!
一.求下列各式的值:
1.
2.
3.
(x≥1)
4.
(x≤1)
二.已知实数a、b、c,在数轴上的位置如下图所示,
试化简:
(1)
-
|a-b|+|c-a|+
(2)|a+b-c|+|b-2c|+
-2
练习题
第四章:实数复习
苏科版
一、概念复方根,算术平方根,
被开方数,根指数,
开平方,开立方,
无理数,实数
正数a的正的平方根也叫做a的算术平方根,
求一个数的平方根(立方根)的运算,叫做开平方(开立方)
。
一般地,如果一个数的平方等于a
,这个数叫做a的平方根。(也叫二次方根)
平方根、算术平方根、立方根的定义
数
的立方根用符号
表示。
一般地,如果
,那么
叫
的立方根
区别
你知道算术平方根、平方根、立方根的区别吗?
算术平方根
平方根
立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(1个)
0
没有
互为相反数(2个)
0
没有
正数(1个)
0
负数(一个)
求一个数的平方根的运算叫开平方
求一个数的立方根的运算叫开立方
≠
是本身
0,1
0
0,1,-1
1.填一填
25的平方根是
;16的算术平方根是
;
27的立方根是
;
的平方根是
,
4
3
针对练习一——平方根
立方根
8
-0.4
0.3
±5
±2
针对练习一——平方根
立方根
2.火眼晴晴选一选
(1)下列说法中正确的是(
)
A.
的平方根是±3
B.1的立方根是±1
C.
=±1
D.
是5的平方根的相反数
(2)下列说法中
①
-4是16的算术平方根
②4是16的算术平方根
③-7是49的算术平方根
④7是(-7)?的算术平方根
其中正确的是(
)
A.
①③
B.
②③
C.
②④
D.
①④
A
C
实数
有理数
无理数
分数
整数
正整数
0
负整数
正分数
负分数
自然数
正无理数
负无理数
无限不循环小数
有限小数及无限循环小数
一般有四种情况
二、分类
针对练习二——实数分类
中无理数的个
A.
2
B.
3
C.
4
D.
5
B
1、在下列各数
数是(
)个
2.
下列说法错误的有(
)个
①无限小数一定是无理数;
②无理数一定是无限小数;
③带根号的数一定是无理数;
④不带根号的数一定是有理数.
A.
1
B.2
C.3
D.4
C
针对练习二——实数分类
无理数集合:
有理数集合:
整数集合:
分数集合:
3.将下列各数分别填入下列的集合括号中
针对练习二——实数分类
1.实数与数轴:实数与数轴上的点__________对应。
2.实数的相反数、绝对值:
相反数:实数a的相反数为______;
绝对值:正数的绝对值是它的本身;负数的绝对值是它的相反数;零的绝对值是零.即实数的绝对值是非负数。
三、实数的相关概念及运算
实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则与运算律对实数仍然适用。
0
一一
的相反数是
;
相反数是
;
;
。
2.
3.如图,以数轴的单位长线段为边做一个正方形,以数轴的原点为圆心,正方形对角线长为半径画弧,交数轴正半轴于点A,则点A表示的数是(
)
A.1.5
B.1.4
C.
D.
C
针对练习三——实数相关概念、运算
-3
1
0
针对练习三——实数相关概念、运算
4.
5.计算
6.求
的值:
方法:(1)利用数轴:在数轴上表示的两个
实数,
。
正数
零
负数。
(2)利用绝对值:
两个负数比较,
。
(3)平方法
(4)分母(子)有理化
(四)实数大小比较
大于
大于
绝对值大的反而小
右边的数总比左边的数大
2.实数
在数轴上的对应点如图所示,
则它们从小到大的顺序是
。
c
d
0
b
针对练习四——实数大小比较
1.下列各数中,最小的数是
(
)
A.-1
B.0
C.1
D.-
D
3.比较下列各组数的大小
知识拓展
掌握规律
注意平方根和立方根的移位法则
五、扩大,缩小
11.8
0.3535
74500
针对练习五——扩大和缩小
3280
328000
1.π的整数部分为3,则它的小数部分是
;
π-3
2
六、无理数的整数部分与小数部分
七、式子有意义
1、在开平方运算中,被开方数具有非负性
2、分母不为0
针对练习七——有意义的条件
7、式子有意义的条件
1、平方根立方根有关概念
2、实数分类
3、实数有关运算
5、扩大、缩小的变化规律
4、实数大小比较
6、明确表示一个数的小数部分和整数部分
总结
谢谢!
一.求下列各式的值:
1.
2.
3.
(x≥1)
4.
(x≤1)
二.已知实数a、b、c,在数轴上的位置如下图所示,
试化简:
(1)
-
|a-b|+|c-a|+
(2)|a+b-c|+|b-2c|+
-2
练习题
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
