苏科版七年级数学下册教学课件-8.3 同底数幂的除法(15张)
文档属性
| 名称 | 苏科版七年级数学下册教学课件-8.3 同底数幂的除法(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 229.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 23:20:04 | ||
图片预览



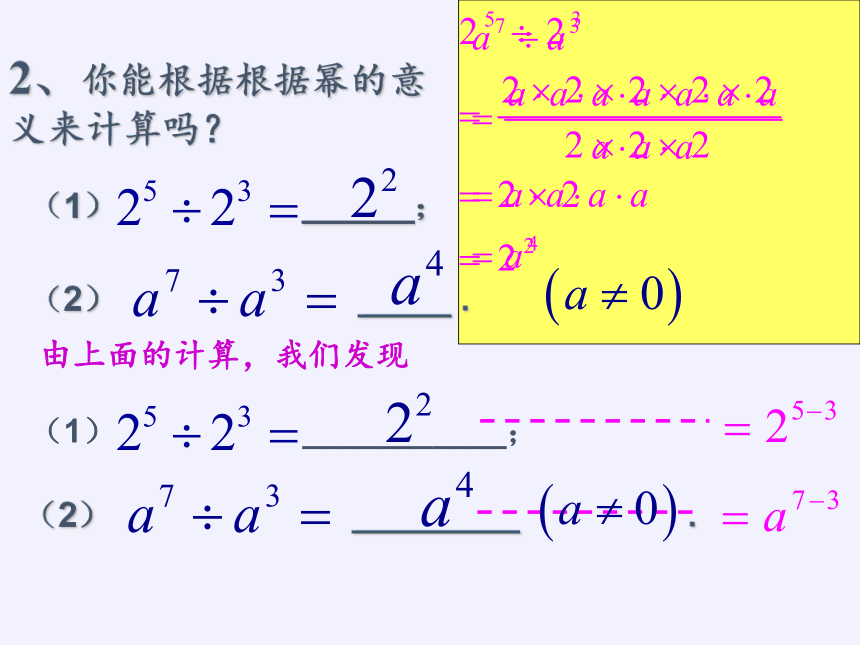



文档简介
(共15张PPT)
8.3
同底数幂的除法
我们知道同底数幂的乘法法则:
那么同底数幂怎么相除呢?
1、你能根据除法是乘法的逆运算来计算吗?
(1)23
·
22
=
25
25
÷
23=___
25
÷
22=___
(2)
a3
·a(
)=a7
a7÷
a3
=___
_______
试一试
猜想
当a≠0,m、n是正整数,且m>n时,试猜想:
am÷an=___.
22
23
∴
am÷an=
∵
an
·
a(
)
=am,
am–n
.
m–n
am–n
a4
4
a7
÷
a4
=
a3
2、你能根据根据幂的意义来计算吗?
(1)
______;
(2)
_____
.
由上面的计算,我们发现
你能发现什么规律?
(1)
___________;
(2)
_________
.
用幂的定义:
am÷an
m个a
n个a
a
·
a
·
…·a
a
·
a
·
…·a
=
n个a
(m-n)个a
a
·
a
·
…·a
a
·
a
·
…·a
=
·
a
·
a
·
…·a
=
am-n
n个a
这就是说,同底数幂相除,底数不变,指数相减。
一般地,设m、n为正整数,且m>n,
有:
总结
典型例题
例1
计算
(1)
(2)
(3)
(4)
解:
(1)
(2)解:
(3)解:
(4)解:
例2
计算
(1)
(2)
(3)
(1)解:
(2)解:
(3)解:
例题解析
.
注意
?
最后结果中幂的形式应是最简的.
①幂的指数、底数都应是最简的;
③幂的底数是积的形式时,要再用一次(ab)n=an
bn.
②底数中系数不能为负;
下面的计算是否正确?如有错误,请改正?
(1)a
8÷a
4=
a
2
(
)
(2)t
10
÷
t
9
=
t
(
)
(3)m
5÷m
=
m
5
(
)
(4)(-z
)
6÷(-z)2
=
-z4
(
)
合作交流
练一练
例3
计算:
(1)p2m+2÷p3(m是正整数)
(2)
p2m+2÷pm-3
(m是正整数)
(3)32m÷3m-1÷32
(m是正整数)
(4)
(5)
(m是正整数)
小结
你觉得在计算时需要注意什么?
练习
1、计算:
(n为正整数)
2、
提高创新题
谢
谢
8.3
同底数幂的除法
我们知道同底数幂的乘法法则:
那么同底数幂怎么相除呢?
1、你能根据除法是乘法的逆运算来计算吗?
(1)23
·
22
=
25
25
÷
23=___
25
÷
22=___
(2)
a3
·a(
)=a7
a7÷
a3
=___
_______
试一试
猜想
当a≠0,m、n是正整数,且m>n时,试猜想:
am÷an=___.
22
23
∴
am÷an=
∵
an
·
a(
)
=am,
am–n
.
m–n
am–n
a4
4
a7
÷
a4
=
a3
2、你能根据根据幂的意义来计算吗?
(1)
______;
(2)
_____
.
由上面的计算,我们发现
你能发现什么规律?
(1)
___________;
(2)
_________
.
用幂的定义:
am÷an
m个a
n个a
a
·
a
·
…·a
a
·
a
·
…·a
=
n个a
(m-n)个a
a
·
a
·
…·a
a
·
a
·
…·a
=
·
a
·
a
·
…·a
=
am-n
n个a
这就是说,同底数幂相除,底数不变,指数相减。
一般地,设m、n为正整数,且m>n,
有:
总结
典型例题
例1
计算
(1)
(2)
(3)
(4)
解:
(1)
(2)解:
(3)解:
(4)解:
例2
计算
(1)
(2)
(3)
(1)解:
(2)解:
(3)解:
例题解析
.
注意
?
最后结果中幂的形式应是最简的.
①幂的指数、底数都应是最简的;
③幂的底数是积的形式时,要再用一次(ab)n=an
bn.
②底数中系数不能为负;
下面的计算是否正确?如有错误,请改正?
(1)a
8÷a
4=
a
2
(
)
(2)t
10
÷
t
9
=
t
(
)
(3)m
5÷m
=
m
5
(
)
(4)(-z
)
6÷(-z)2
=
-z4
(
)
合作交流
练一练
例3
计算:
(1)p2m+2÷p3(m是正整数)
(2)
p2m+2÷pm-3
(m是正整数)
(3)32m÷3m-1÷32
(m是正整数)
(4)
(5)
(m是正整数)
小结
你觉得在计算时需要注意什么?
练习
1、计算:
(n为正整数)
2、
提高创新题
谢
谢
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
