鲁教版九年级数学下册5.4圆周角和圆心角的关系 课时训练(Word版 无答案)
文档属性
| 名称 | 鲁教版九年级数学下册5.4圆周角和圆心角的关系 课时训练(Word版 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 137.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 23:19:55 | ||
图片预览

文档简介
5.4
圆周角和圆心角的关系
同步训练
如图,⊙O的直径AB垂直于弦CD,垂足是点E,∠CAO=22.5°,OC=6,则CD的长为( )
A.
6
B.
3
C.
6
D.
12
如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )
A.
B.
C.
D.
如图,点A,B,C在⊙O上,若∠ACB=112°,则∠α=( )
A.
68°
B.
112°
C.
136°
D.
134°
如图,A,B,C三点在⊙O上,且∠BOC=100°,则∠A的度数为( )
A.
40°
B.
50°
C.
80°
D.
100°
如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( )
A.
OC∥BD
B.
AD⊥OC
C.
△CEF≌△BED
D.
AF=FD
如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是( )
A.
75°
B.
70°
C.
65°
D.
35°
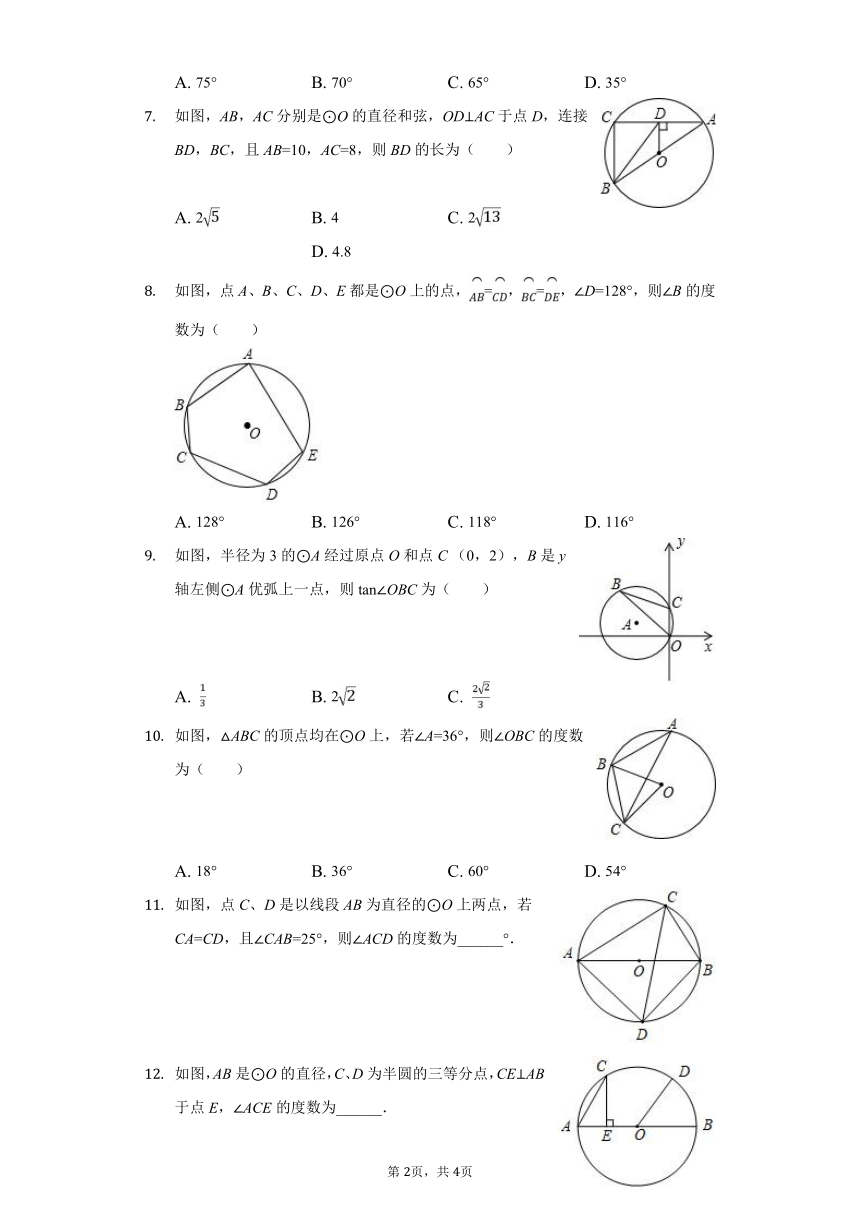
如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D,连接BD,BC,且AB=10,AC=8,则BD的长为( )
A.
2
B.
4
C.
2
D.
4.8
如图,点A、B、C、D、E都是⊙O上的点,=,=,∠D=128°,则∠B的度数为( )
???????
A.
128°
B.
126°
C.
118°
D.
116°
如图,半径为3的⊙A经过原点O和点C?(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A.
B.
2
C.
D.
如图,△ABC的顶点均在⊙O上,若∠A=36°,则∠OBC的度数为( )
A.
18°
B.
36°
C.
60°
D.
54°
如图,点C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠CAB=25°,则∠ACD的度数为______°.
如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为______.
如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=______度.
如图,点A、B、C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为______.
如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE为______.
三、解答题(本大题共3小题,共24.0分)
如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D为边BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=30°.
(1)求∠BAD的度数;
(2)若AD=,求DB的长.
如图,AB为⊙O的直径,C为⊙O上一点,D是弧BC的中点,BC与AD、OD分别交于点E、F.
(1)求证:DO∥AC;
(2)求证:DE?DA=DC2;
(3)若tan∠CAD=,求sin∠CDA的值.
第2页,共2页
第1页,共1页
圆周角和圆心角的关系
同步训练
如图,⊙O的直径AB垂直于弦CD,垂足是点E,∠CAO=22.5°,OC=6,则CD的长为( )
A.
6
B.
3
C.
6
D.
12
如图,AB是⊙O的直径,点C和点D是⊙O上位于直径AB两侧的点,连接AC,AD,BD,CD,若⊙O的半径是13,BD=24,则sin∠ACD的值是( )
A.
B.
C.
D.
如图,点A,B,C在⊙O上,若∠ACB=112°,则∠α=( )
A.
68°
B.
112°
C.
136°
D.
134°
如图,A,B,C三点在⊙O上,且∠BOC=100°,则∠A的度数为( )
A.
40°
B.
50°
C.
80°
D.
100°
如图,AB是⊙O的直径,C,D是⊙O上的两点,且BC平分∠ABD,AD分别与BC,OC相交于点E,F,则下列结论不一定成立的是( )
A.
OC∥BD
B.
AD⊥OC
C.
△CEF≌△BED
D.
AF=FD
如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是( )
A.
75°
B.
70°
C.
65°
D.
35°
如图,AB,AC分别是⊙O的直径和弦,OD⊥AC于点D,连接BD,BC,且AB=10,AC=8,则BD的长为( )
A.
2
B.
4
C.
2
D.
4.8
如图,点A、B、C、D、E都是⊙O上的点,=,=,∠D=128°,则∠B的度数为( )
???????
A.
128°
B.
126°
C.
118°
D.
116°
如图,半径为3的⊙A经过原点O和点C?(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为( )
A.
B.
2
C.
D.
如图,△ABC的顶点均在⊙O上,若∠A=36°,则∠OBC的度数为( )
A.
18°
B.
36°
C.
60°
D.
54°
如图,点C、D是以线段AB为直径的⊙O上两点,若CA=CD,且∠CAB=25°,则∠ACD的度数为______°.
如图,AB是⊙O的直径,C、D为半圆的三等分点,CE⊥AB于点E,∠ACE的度数为______.
如图,已知AB是⊙O的弦,半径OC垂直AB,点D是⊙O上一点,且点D与点C位于弦AB两侧,连接AD、CD、OB,若∠BOC=70°,则∠ADC=______度.
如图,点A、B、C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为______.
如图,AB是半圆O的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE为______.
三、解答题(本大题共3小题,共24.0分)
如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D为边BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长;
如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=30°.
(1)求∠BAD的度数;
(2)若AD=,求DB的长.
如图,AB为⊙O的直径,C为⊙O上一点,D是弧BC的中点,BC与AD、OD分别交于点E、F.
(1)求证:DO∥AC;
(2)求证:DE?DA=DC2;
(3)若tan∠CAD=,求sin∠CDA的值.
第2页,共2页
第1页,共1页
