沪科版九年级数学上册第21章二次函数与反比例函数单元综合测试题(word版含答案)
文档属性
| 名称 | 沪科版九年级数学上册第21章二次函数与反比例函数单元综合测试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 663.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 15:25:41 | ||
图片预览



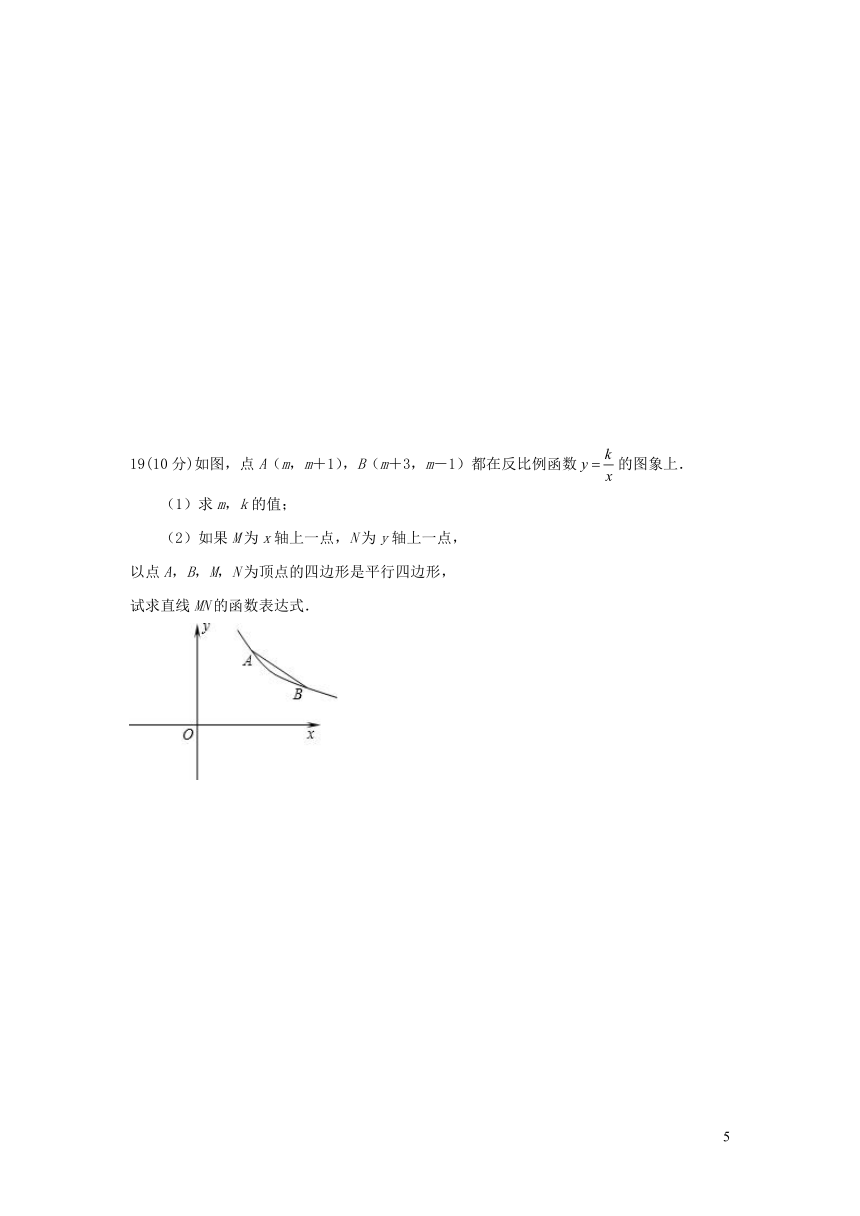
文档简介
第21章
二次函数和反比例函数单元测试题(2)
班级:
姓名:
学号:
得分:
一.选择题(10×4)
1.二次函数的最小值是(
)
A.
B.
C.
D.
2.如图,抛物线的对称轴是直线,且经过点(3,0),则的值为
A.
0
B.
-1
C.
1
D.
2
3.二次函数的图象的顶点坐标是(
)
A.
B.
C.
D.
4.函数在同一直角坐标系内的图象大致是
(
)
5.将一张边长为30㎝的正方形纸片的四角分别剪去一个边长为x㎝的小正方形,然后折叠成一个无盖的长方体.当x取下面哪个数值时,长方体的体积最大
A.
7
B.
6
C.
5
D.
4
6.下列命题:
①若,则;
②若,则一元二次方程有两个不相等的实数根;
③若,则一元二次方程有两个不相等的实数根;
④若,则二次函数的图象与坐标轴的公共点的个数是2或3.
其中正确的是( ).
A.只有①②③
B.只有①③④
C.只有①④
D.
只有②③④.
7.如图所示是二次函数的图象在轴上方的一部分,对于这段图象与轴所围成的阴影部分的面积,你认为与其最接近的值是(
)
A.4
B.
C.
D.
8.在平面直角坐标系中,如果抛物线y=2x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是
A.y=2(x-2)2
+
2
B.y=2(x
+
2)2-2
C.y=2(x-2)2-2
D.y=2(x
+
2)2
+
2
9.如图,正方形的边长为2,反比例函数过点,则的值是(
)
A.
B.
C.
D.
10.一个函数的图象如图,给出以下结论:
①当时,函数值最大;
②当时,函数随的增大而减小;
③存在,当时,函数值为0.
其中正确的结论是(
)
A.①②
B.①③
C.②③
D.①②③
二、填空题(5×5)
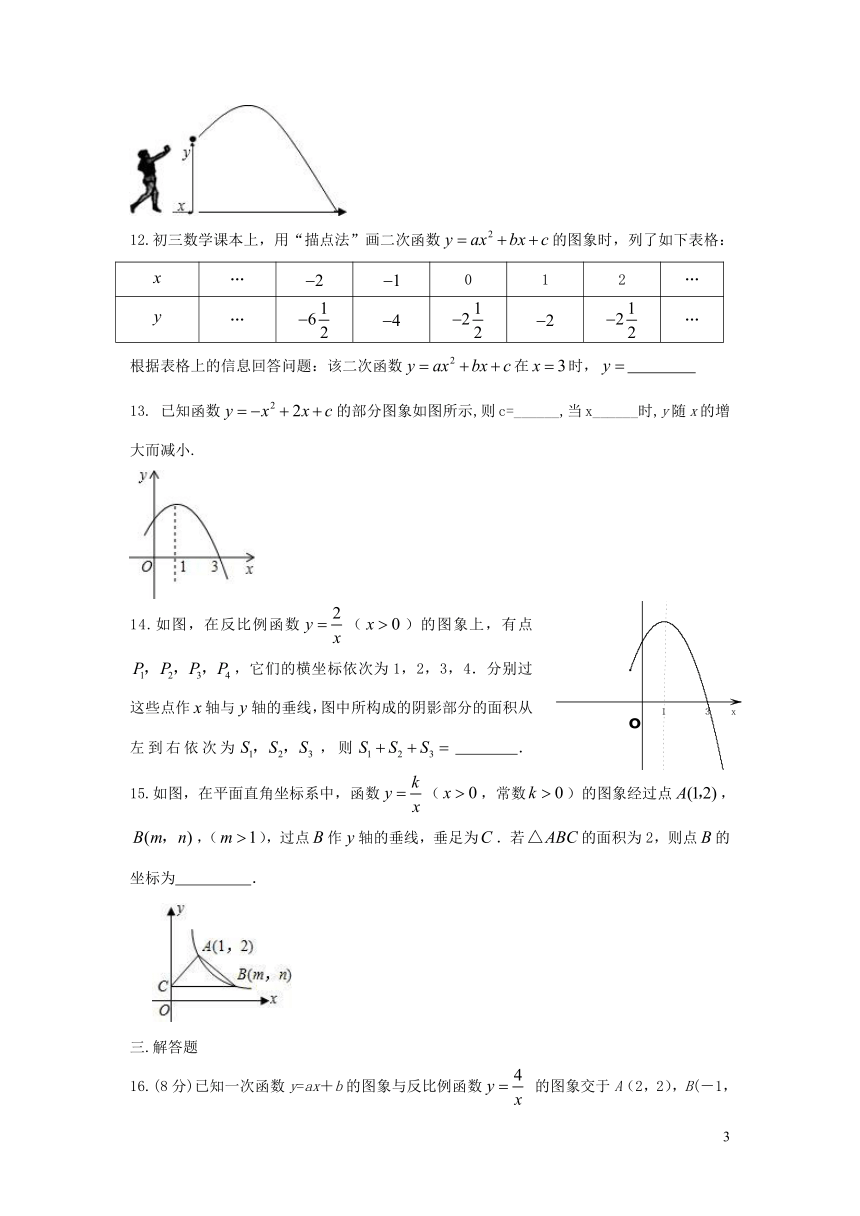
11.如图,一名男生推铅球,铅球行进高度(单位:m)与水平距离(单位:m)之间的关系是.则他将铅球推出的距离是
m.
12.初三数学课本上,用“描点法”画二次函数的图象时,列了如下表格:
…
0
1
2
…
…
…
根据表格上的信息回答问题:该二次函数在时,
13.
已知函数的部分图象如图所示,则c=______,当x______时,y随x的增大而减小.
14.如图,在反比例函数()的图象上,有点,它们的横坐标依次为1,2,3,4.分别过这些点作轴与轴的垂线,图中所构成的阴影部分的面积从左到右依次为,则
.
15.如图,在平面直角坐标系中,函数(,常数)的图象经过点,,(),过点作轴的垂线,垂足为.若的面积为2,则点的坐标为
.
三.解答题
16.(8分)已知一次函数y=ax+b的图象与反比例函数
的图象交于A(2,2),B(-1,m),求一次函数的解析式.
17.(8分)已知二次函数y=x2-2x-1。
(2)求此二次函数的图象与x轴的交点坐标.
(2)
将y=x2的图象经过怎样的平移,就可以得到二次函数y=x2-2x-1的图象
18.(11分)已知二次函数中,函数与自变量的部分对应值如下表:
…
…
…
…
(1)求该二次函数的关系式;
(2)当为何值时,有最小值,最小值是多少?
(3)※若,两点都在该函数的图象上,试比较与的大小.
19(10分)如图,点A(m,m+1),B(m+3,m-1)都在反比例函数的图象上.
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点,
以点A,B,M,N为顶点的四边形是平行四边形,
试求直线MN的函数表达式.
20.(10分)已知一次函数与反比例函数的图象交于点.
(1)求这两个函数的函数关系式;
(2)在给定的直角坐标系(如图)中,画出这两个函数的大致图象;
(3)当为何值时,一次函数的值大于反比例函数的值?当为何值时,一次函数的值小于反比例函数的值?
21.(12分)某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加元.求:
(1)房间每天的入住量(间)关于(元)的函数关系式.(3分)
(2)该宾馆每天的房间收费(元)关于(元)的函数关系式.(3分)
(3)该宾馆客房部每天的利润(元)关于(元)的函数关系式;当每个房间的定价为每天多少元时,有最大值?最大值是多少?(6分)
22.(12分)桂林红桥位于桃花江上,是桂林两江四湖的一道亮丽的风景线,该桥的部分横截面如图所示,上方可看作是一个经过A、C、B三点的抛物线,以桥面的水平线为X轴,经过抛物线的顶点C与X轴垂直的直线为Y轴,建立直角坐标系,已知此桥垂直于桥面的相邻两柱之间距离为2米(图中用线段AD、CO、BE等表示桥柱)CO=1米,FG=2米
(1)求经过A、B、C三点的抛物线的解析式。
(2)求柱子AD的高度。
型
号
甲
乙
丙
进价(万元/台)
0.9
1.2
1.1
售价(万元/台)
1.2
1.6
1.3
23.(14分)“5?12”汶川大地震后,某健身器材销售公司通过当地“红十字会”向灾区献爱心,捐出了五月份全部销售利润.已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进货款64万元和其他各项支出(含人员工资和杂项开支)3.8万元.这三种器材的进价和售价如下表,人员工资y1(万元)和杂项支出y2(万元)分别与总销售量x(台)成一次函数关系(如图).
(1)求y1与x的函数解析式;
(2)求五月份该公司的总销售量;
(3)设公司五月份售出甲种型号器材t台,五月份总销售利为W(万元),求W与t的函数关系式;(销售利润=销售额-进价-其他各项支出)
(4)请推测该公司这次向灾区捐款金额的最大值.
参考答案
一、选择题BAACC
BCBDC二、填空题11.10
,12.-4
,13.
3
x>1
,14.
,15.(3,)
三、解答题
16.先求得m=-4,∵一次函数y=ax+b的图象过点A(2,2)B(-1,-4)
∴
解得
a=2
,b=-2
∴所求一次函数的解析式为y=2x-2
17.⑴解方程
x2-2x-1=0得x=1±∴二次函数y=x2-2x-1与x轴的交点坐标为(1+,0),(1-,0)
⑵y=x2-2x-1=(x-1)2-2
顶点坐标为(1,-2)
∴把y=x2向右平移1个单位再向下平移2单位就可以得到y=x2-2x-1的图象
18.(1)根据题意,当时,;当时,.
所以
解得
所以,该二次函数关系式为.
(2)因为,
所以当时,有最小值,最小值是1.
(3)因为,两点都在函数的图象上,
所以,,.
.所以,当,即时,;
当,即时,;
当,即时,.
19.解:(1)由题意可知,.
解,得
m=3.
………………………………3分
∴
A(3,4),B(6,2);
∴
k=4×3=12.
……………………………4分
(2)存在两种情况,如图:
①当M点在x轴的正半轴上,N点在y轴的正半轴
上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵
四边形AN1M1B为平行四边形,
∴
线段N1M1可看作由线段AB向左平移3个单位,
再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).
由(1)知A点坐标为(3,4),B点坐标为(6,2),
∴
N1点坐标为(0,4-2),即N1(0,2);
M1点坐标为(6-3,0),即M1(3,0).
设直线M1N1的函数表达式为,把x=3,y=0代入,解得.
∴
直线M1N1的函数表达式为.
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵
AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴
N1M1∥M2N2,N1M1=M2N2.
∴
线段M2N2与线段N1M1关于原点O成中心对称.
∴
M2点坐标为(-3,0),N2点坐标为(0,-2).
设直线M2N2的函数表达式为,把x=-3,y=0代入,解得,
∴
直线M2N2的函数表达式为.
所以,直线MN的函数表达式为或.
20.(1)设一次函数的关系式为,反比例函数的关系式为,
反比例函数的图象经过点,
.
所求反比例函数的关系式为.
将点的坐标代入上式得,
点的坐标为.
由于一次函数的图象过
和,
解得
所求一次函数的关系式为.
(2)两个函数的大致图象如图.
(3)由两个函数的图象可以看出.
当和时,一次函数的值大于反比例函数的值.
当和时,一次函数的值小于反比例函数的值.
21.
22.⑴根据题意
可设所求函数解析式为:y=ax2+1,∵它过点F(-4,2)
∴2=16a+1
a=
∴所求抛物线的解析式为Y=x2+1
⑵把x=-8代入Y=x2+1得y=×64+1=5
∴
柱子AD的高度为5米.
23.
x
y
C
O
A
B
x
y
O
P1
P2
P3
P4
1
2
3
4
O
1
2
3
4
5
6
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-1
-2
-3
-4
-5
-6
x
y
0
20
0.2
0.3
1.2
B
y1
y2=0.005x+0.3
x(台)
y(万元)
x
O
y
A
B
M1
N1
M2
N2
O
1
2
3
4
5
6
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-1
-2
-3
-4
-5
-6
x
y
Q(2,-3)
P(-3,2)
12
二次函数和反比例函数单元测试题(2)
班级:
姓名:
学号:
得分:
一.选择题(10×4)
1.二次函数的最小值是(
)
A.
B.
C.
D.
2.如图,抛物线的对称轴是直线,且经过点(3,0),则的值为
A.
0
B.
-1
C.
1
D.
2
3.二次函数的图象的顶点坐标是(
)
A.
B.
C.
D.
4.函数在同一直角坐标系内的图象大致是
(
)
5.将一张边长为30㎝的正方形纸片的四角分别剪去一个边长为x㎝的小正方形,然后折叠成一个无盖的长方体.当x取下面哪个数值时,长方体的体积最大
A.
7
B.
6
C.
5
D.
4
6.下列命题:
①若,则;
②若,则一元二次方程有两个不相等的实数根;
③若,则一元二次方程有两个不相等的实数根;
④若,则二次函数的图象与坐标轴的公共点的个数是2或3.
其中正确的是( ).
A.只有①②③
B.只有①③④
C.只有①④
D.
只有②③④.
7.如图所示是二次函数的图象在轴上方的一部分,对于这段图象与轴所围成的阴影部分的面积,你认为与其最接近的值是(
)
A.4
B.
C.
D.
8.在平面直角坐标系中,如果抛物线y=2x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是
A.y=2(x-2)2
+
2
B.y=2(x
+
2)2-2
C.y=2(x-2)2-2
D.y=2(x
+
2)2
+
2
9.如图,正方形的边长为2,反比例函数过点,则的值是(
)
A.
B.
C.
D.
10.一个函数的图象如图,给出以下结论:
①当时,函数值最大;
②当时,函数随的增大而减小;
③存在,当时,函数值为0.
其中正确的结论是(
)
A.①②
B.①③
C.②③
D.①②③
二、填空题(5×5)
11.如图,一名男生推铅球,铅球行进高度(单位:m)与水平距离(单位:m)之间的关系是.则他将铅球推出的距离是
m.
12.初三数学课本上,用“描点法”画二次函数的图象时,列了如下表格:
…
0
1
2
…
…
…
根据表格上的信息回答问题:该二次函数在时,
13.
已知函数的部分图象如图所示,则c=______,当x______时,y随x的增大而减小.
14.如图,在反比例函数()的图象上,有点,它们的横坐标依次为1,2,3,4.分别过这些点作轴与轴的垂线,图中所构成的阴影部分的面积从左到右依次为,则
.
15.如图,在平面直角坐标系中,函数(,常数)的图象经过点,,(),过点作轴的垂线,垂足为.若的面积为2,则点的坐标为
.
三.解答题
16.(8分)已知一次函数y=ax+b的图象与反比例函数
的图象交于A(2,2),B(-1,m),求一次函数的解析式.
17.(8分)已知二次函数y=x2-2x-1。
(2)求此二次函数的图象与x轴的交点坐标.
(2)
将y=x2的图象经过怎样的平移,就可以得到二次函数y=x2-2x-1的图象
18.(11分)已知二次函数中,函数与自变量的部分对应值如下表:
…
…
…
…
(1)求该二次函数的关系式;
(2)当为何值时,有最小值,最小值是多少?
(3)※若,两点都在该函数的图象上,试比较与的大小.
19(10分)如图,点A(m,m+1),B(m+3,m-1)都在反比例函数的图象上.
(1)求m,k的值;
(2)如果M为x轴上一点,N为y轴上一点,
以点A,B,M,N为顶点的四边形是平行四边形,
试求直线MN的函数表达式.
20.(10分)已知一次函数与反比例函数的图象交于点.
(1)求这两个函数的函数关系式;
(2)在给定的直角坐标系(如图)中,画出这两个函数的大致图象;
(3)当为何值时,一次函数的值大于反比例函数的值?当为何值时,一次函数的值小于反比例函数的值?
21.(12分)某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加元.求:
(1)房间每天的入住量(间)关于(元)的函数关系式.(3分)
(2)该宾馆每天的房间收费(元)关于(元)的函数关系式.(3分)
(3)该宾馆客房部每天的利润(元)关于(元)的函数关系式;当每个房间的定价为每天多少元时,有最大值?最大值是多少?(6分)
22.(12分)桂林红桥位于桃花江上,是桂林两江四湖的一道亮丽的风景线,该桥的部分横截面如图所示,上方可看作是一个经过A、C、B三点的抛物线,以桥面的水平线为X轴,经过抛物线的顶点C与X轴垂直的直线为Y轴,建立直角坐标系,已知此桥垂直于桥面的相邻两柱之间距离为2米(图中用线段AD、CO、BE等表示桥柱)CO=1米,FG=2米
(1)求经过A、B、C三点的抛物线的解析式。
(2)求柱子AD的高度。
型
号
甲
乙
丙
进价(万元/台)
0.9
1.2
1.1
售价(万元/台)
1.2
1.6
1.3
23.(14分)“5?12”汶川大地震后,某健身器材销售公司通过当地“红十字会”向灾区献爱心,捐出了五月份全部销售利润.已知该公司五月份只售出甲、乙、丙三种型号器材若干台,每种型号器材不少于8台,五月份支出包括这批器材进货款64万元和其他各项支出(含人员工资和杂项开支)3.8万元.这三种器材的进价和售价如下表,人员工资y1(万元)和杂项支出y2(万元)分别与总销售量x(台)成一次函数关系(如图).
(1)求y1与x的函数解析式;
(2)求五月份该公司的总销售量;
(3)设公司五月份售出甲种型号器材t台,五月份总销售利为W(万元),求W与t的函数关系式;(销售利润=销售额-进价-其他各项支出)
(4)请推测该公司这次向灾区捐款金额的最大值.
参考答案
一、选择题BAACC
BCBDC二、填空题11.10
,12.-4
,13.
3
x>1
,14.
,15.(3,)
三、解答题
16.先求得m=-4,∵一次函数y=ax+b的图象过点A(2,2)B(-1,-4)
∴
解得
a=2
,b=-2
∴所求一次函数的解析式为y=2x-2
17.⑴解方程
x2-2x-1=0得x=1±∴二次函数y=x2-2x-1与x轴的交点坐标为(1+,0),(1-,0)
⑵y=x2-2x-1=(x-1)2-2
顶点坐标为(1,-2)
∴把y=x2向右平移1个单位再向下平移2单位就可以得到y=x2-2x-1的图象
18.(1)根据题意,当时,;当时,.
所以
解得
所以,该二次函数关系式为.
(2)因为,
所以当时,有最小值,最小值是1.
(3)因为,两点都在函数的图象上,
所以,,.
.所以,当,即时,;
当,即时,;
当,即时,.
19.解:(1)由题意可知,.
解,得
m=3.
………………………………3分
∴
A(3,4),B(6,2);
∴
k=4×3=12.
……………………………4分
(2)存在两种情况,如图:
①当M点在x轴的正半轴上,N点在y轴的正半轴
上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵
四边形AN1M1B为平行四边形,
∴
线段N1M1可看作由线段AB向左平移3个单位,
再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).
由(1)知A点坐标为(3,4),B点坐标为(6,2),
∴
N1点坐标为(0,4-2),即N1(0,2);
M1点坐标为(6-3,0),即M1(3,0).
设直线M1N1的函数表达式为,把x=3,y=0代入,解得.
∴
直线M1N1的函数表达式为.
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵
AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴
N1M1∥M2N2,N1M1=M2N2.
∴
线段M2N2与线段N1M1关于原点O成中心对称.
∴
M2点坐标为(-3,0),N2点坐标为(0,-2).
设直线M2N2的函数表达式为,把x=-3,y=0代入,解得,
∴
直线M2N2的函数表达式为.
所以,直线MN的函数表达式为或.
20.(1)设一次函数的关系式为,反比例函数的关系式为,
反比例函数的图象经过点,
.
所求反比例函数的关系式为.
将点的坐标代入上式得,
点的坐标为.
由于一次函数的图象过
和,
解得
所求一次函数的关系式为.
(2)两个函数的大致图象如图.
(3)由两个函数的图象可以看出.
当和时,一次函数的值大于反比例函数的值.
当和时,一次函数的值小于反比例函数的值.
21.
22.⑴根据题意
可设所求函数解析式为:y=ax2+1,∵它过点F(-4,2)
∴2=16a+1
a=
∴所求抛物线的解析式为Y=x2+1
⑵把x=-8代入Y=x2+1得y=×64+1=5
∴
柱子AD的高度为5米.
23.
x
y
C
O
A
B
x
y
O
P1
P2
P3
P4
1
2
3
4
O
1
2
3
4
5
6
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-1
-2
-3
-4
-5
-6
x
y
0
20
0.2
0.3
1.2
B
y1
y2=0.005x+0.3
x(台)
y(万元)
x
O
y
A
B
M1
N1
M2
N2
O
1
2
3
4
5
6
6
5
4
3
2
1
-1
-2
-3
-4
-5
-6
-1
-2
-3
-4
-5
-6
x
y
Q(2,-3)
P(-3,2)
12
