华东师大版八年级上册13.5.3角平分线的性质与判定(共21张ppt)
文档属性
| 名称 | 华东师大版八年级上册13.5.3角平分线的性质与判定(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 277.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 06:03:18 | ||
图片预览


文档简介
(共21张PPT)
13.5.3角平分线的性质
回忆
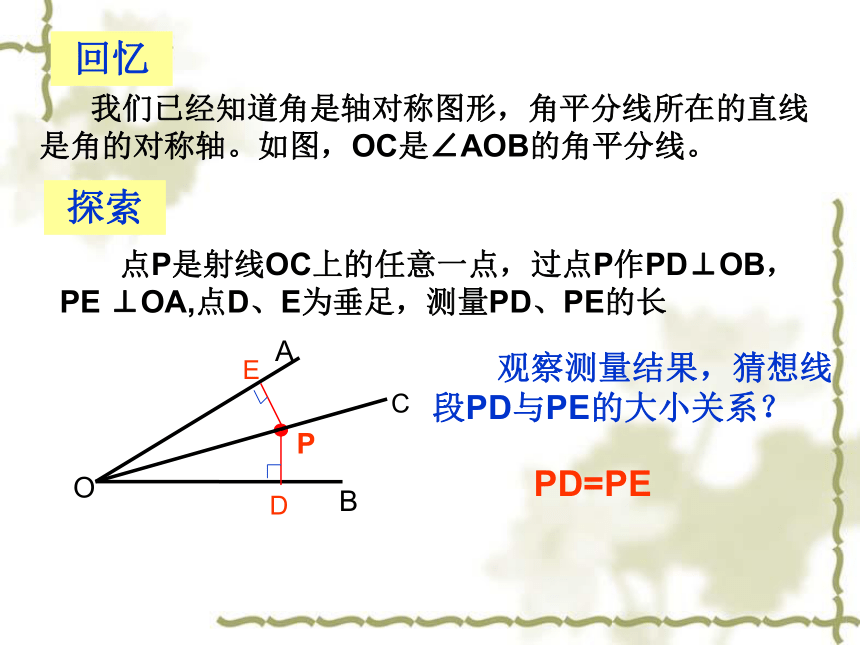
我们已经知道角是轴对称图形,角平分线所在的直线是角的对称轴。如图,OC是∠AOB的角平分线。
探索
点P是射线OC上的任意一点,过点P作PD⊥OB,PE
⊥OA,点D、E为垂足,测量PD、PE的长
P
A
O
B
C
E
D
观察测量结果,猜想线段PD与PE的大小关系?
PD=PE
结论:角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
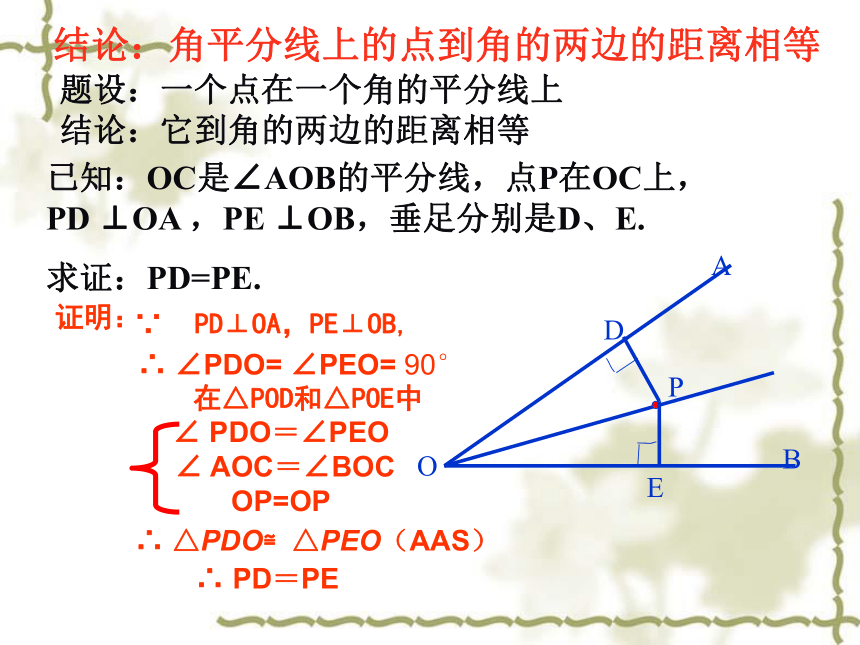
已知:OC是∠AOB的平分线,点P在OC上,PD
⊥OA
,PE
⊥OB,垂足分别是D、E.
求证:PD=PE.
A
O
B
P
E
D
∵
PD⊥OA,PE⊥OB,
证明:
∴
∠PDO=
∠PEO=
90°
在△POD和△POE中
∴
△PDO≌△PEO(AAS)
∠
PDO=∠PEO
∠
AOC=∠BOC
OP=OP
∴
PD=PE
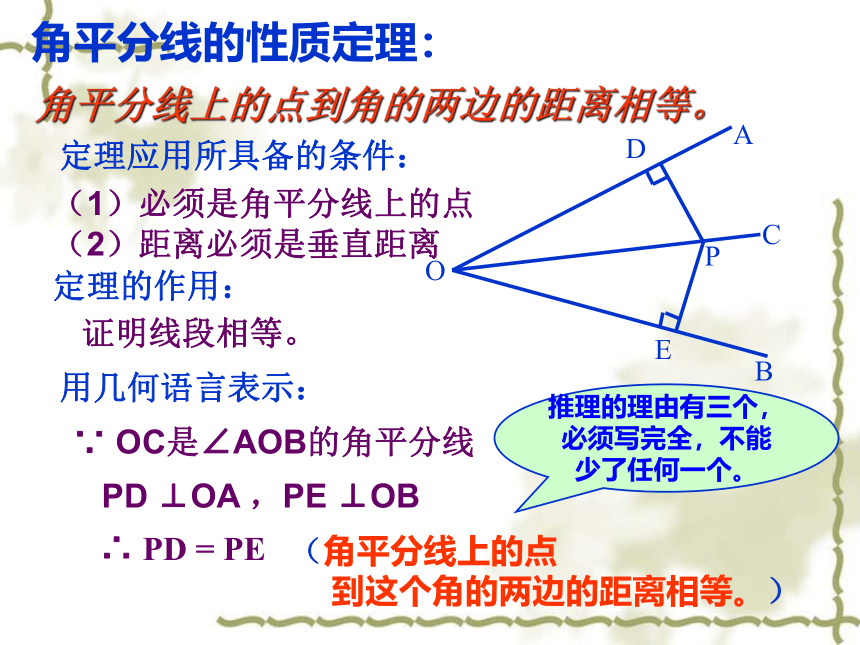
角平分线的性质定理:
角平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
定理的作用:
证明线段相等。
用几何语言表示:
∴
PD
=
PE
(角平分线上的点
到这个角的两边的距离相等。)
推理的理由有三个,必须写完全,不能少了任何一个。
(2)距离必须是垂直距离
(1)必须是角平分线上的点
∵
OC是∠AOB的角平分线
PD
⊥OA
,PE
⊥OB
∵
如图,AD平分∠BAC(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
练习:
判断
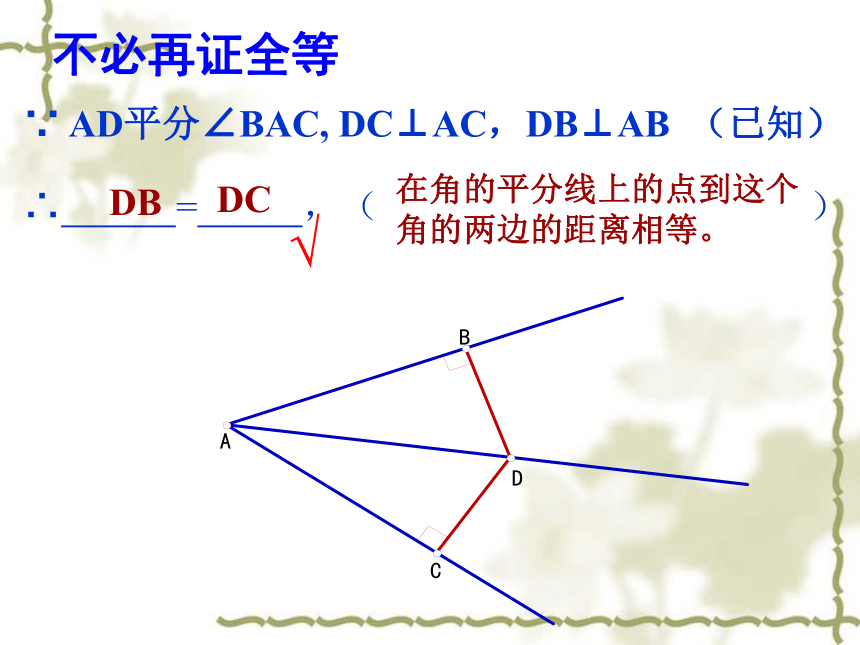
∵
AD平分∠BAC,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
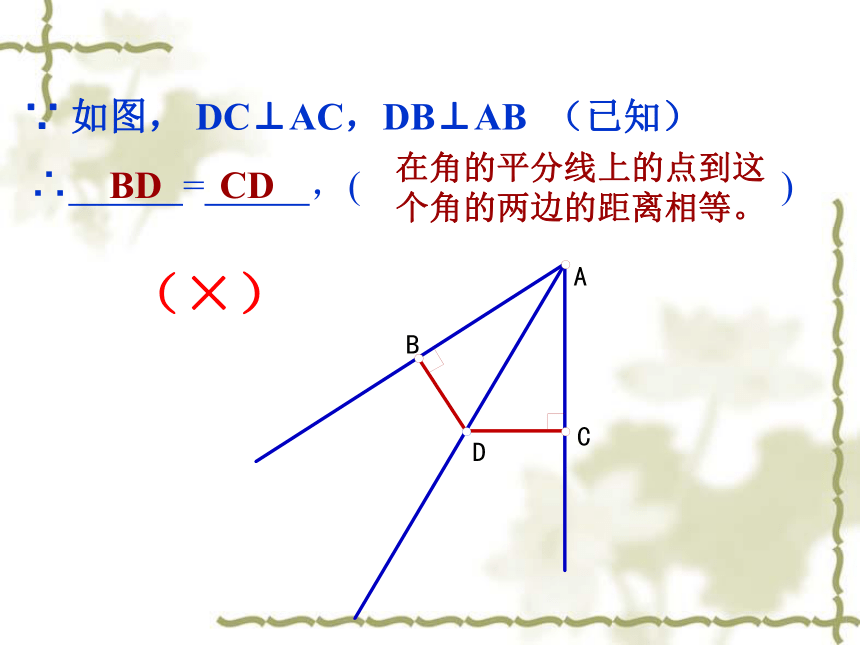
∵
如图,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
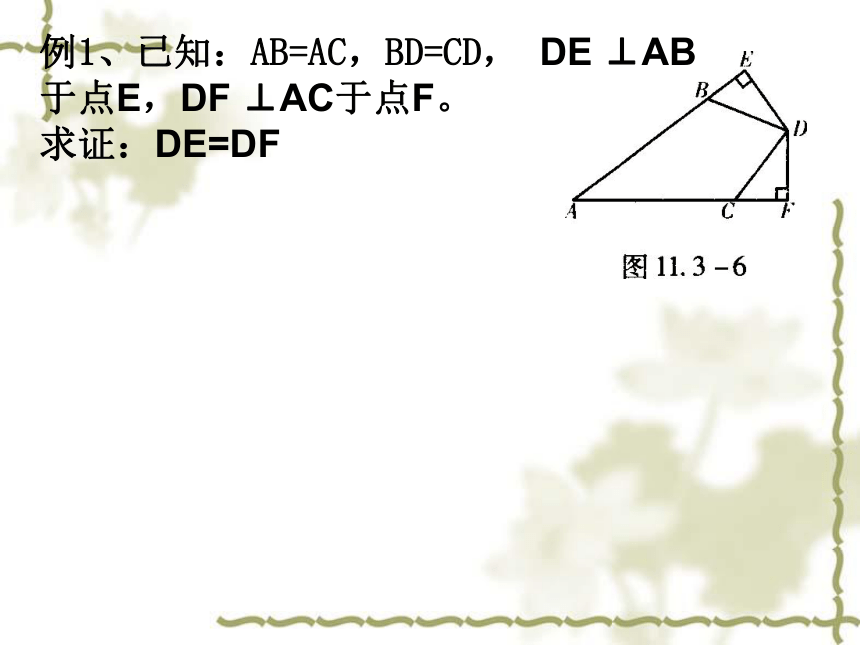
例1、已知:AB=AC,BD=CD,
DE
⊥AB于点E,DF
⊥AC于点F。
求证:DE=DF
,
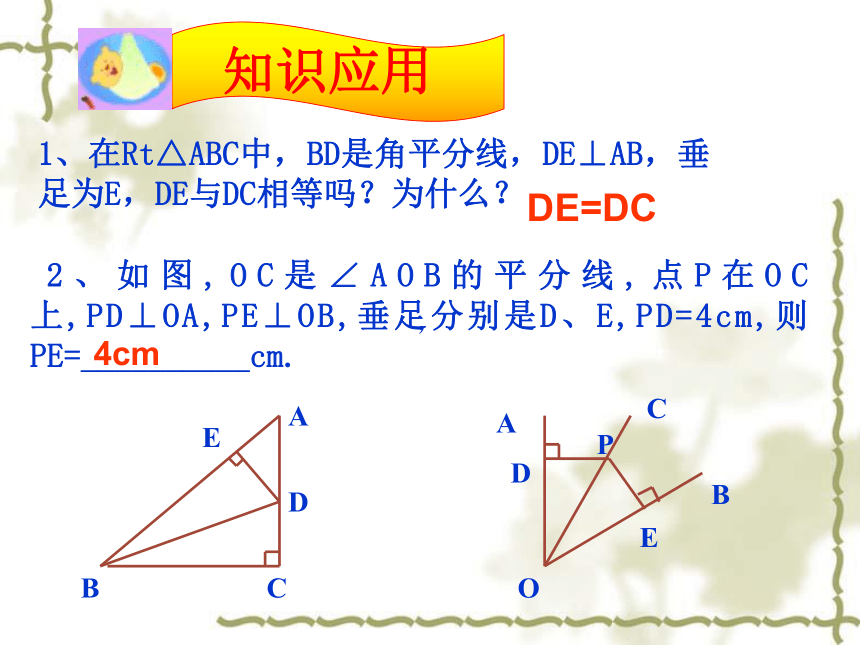
1、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
A
B
C
D
E
2、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
知识应用
DE=DC
4cm
3、如图在△ABC中∠C=900,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E。
.
(1)若AC=6cm,则DE+BD=
。
(2)若AB=10cm,△DBE的周长=
。
6cm
10cm
反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢?
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
思考
证明:
∵
QD⊥OA,QE⊥OB(已知),
∴
∠QDO=∠QEO=90°(垂直的定义)
在Rt△QDO和Rt△QEO中
QO=QO(公共边)
QD=QE
∴
Rt△QDO≌Rt△QEO(HL)
∴
∠
QOD=∠QOE
∴点Q在∠AOB的平分线上
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
这样,我们又可以得到一个结论:
到角两边距离相等的点在角的平分线上。
B
A
D
O
P
E
C
∵
PD⊥OA,PE⊥OB,PD=PE
∴点Q在∠AOB的平分线上.
用几何语言表示:
例
已知:如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
A
B
C
P
M
N
A
B
C
P
M
N
例
已知:如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD
、PE、PF分别垂直于AB、
BC、CA,垂足分别为D、E、F
F
D
E
D
E
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
同理
PE=PF.
∴
PD=PE=PF.
即点P到边AB、BC、
CA的距离相等
想一想,点P在∠A
的
平分线上吗?这说明三角形的三条角平分线有什么关系?
三角形的三条角平分线相交于一点。
例2、如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是点E,F,且BE=CF。
求证:AD是△ABC的角平分线。
A
B
C
E
F
D
练习
教材P98练习1
2
1、如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等.
C●
D●
A
B
O
拓展与延伸
2、如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
3、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:(
)
A.一处
B.
两处
C.三处
D.四处
分析:由于没有限制在何处选址,故要求的地址共有四处。
D
小结:
1:画一个已知角的角平分线;
及画一条已知直线的垂线;
2:角平分线的性质:
角的平分线上的点到角的两边的距离相等.
3:角平分线的判定结论:
到角的两边的距离相等的点在角平分线上。
练习
教材P99习题2,3,4,5
13.5.3角平分线的性质
回忆
我们已经知道角是轴对称图形,角平分线所在的直线是角的对称轴。如图,OC是∠AOB的角平分线。
探索
点P是射线OC上的任意一点,过点P作PD⊥OB,PE
⊥OA,点D、E为垂足,测量PD、PE的长
P
A
O
B
C
E
D
观察测量结果,猜想线段PD与PE的大小关系?
PD=PE
结论:角平分线上的点到角的两边的距离相等
题设:一个点在一个角的平分线上
结论:它到角的两边的距离相等
已知:OC是∠AOB的平分线,点P在OC上,PD
⊥OA
,PE
⊥OB,垂足分别是D、E.
求证:PD=PE.
A
O
B
P
E
D
∵
PD⊥OA,PE⊥OB,
证明:
∴
∠PDO=
∠PEO=
90°
在△POD和△POE中
∴
△PDO≌△PEO(AAS)
∠
PDO=∠PEO
∠
AOC=∠BOC
OP=OP
∴
PD=PE
角平分线的性质定理:
角平分线上的点到角的两边的距离相等。
B
A
D
O
P
E
C
定理应用所具备的条件:
定理的作用:
证明线段相等。
用几何语言表示:
∴
PD
=
PE
(角平分线上的点
到这个角的两边的距离相等。)
推理的理由有三个,必须写完全,不能少了任何一个。
(2)距离必须是垂直距离
(1)必须是角平分线上的点
∵
OC是∠AOB的角平分线
PD
⊥OA
,PE
⊥OB
∵
如图,AD平分∠BAC(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
练习:
判断
∵
AD平分∠BAC,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
DB
DC
在角的平分线上的点到这个角的两边的距离相等。
√
不必再证全等
∵
如图,
DC⊥AC,DB⊥AB
(已知)
∴
=
,(
)
在角的平分线上的点到这个角的两边的距离相等。
BD
CD
(×)
例1、已知:AB=AC,BD=CD,
DE
⊥AB于点E,DF
⊥AC于点F。
求证:DE=DF
,
1、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
A
B
C
D
E
2、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
知识应用
DE=DC
4cm
3、如图在△ABC中∠C=900,AC=BC,AD平分∠CAB,交BC于点D,DE⊥AB于点E。
.
(1)若AC=6cm,则DE+BD=
。
(2)若AB=10cm,△DBE的周长=
。
6cm
10cm
反过来,到一个角的两边的距离相等的点是否一定在这个角的平分线上呢?
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
思考
证明:
∵
QD⊥OA,QE⊥OB(已知),
∴
∠QDO=∠QEO=90°(垂直的定义)
在Rt△QDO和Rt△QEO中
QO=QO(公共边)
QD=QE
∴
Rt△QDO≌Rt△QEO(HL)
∴
∠
QOD=∠QOE
∴点Q在∠AOB的平分线上
已知:如图,QD⊥OA,QE⊥OB,
点D、E为垂足,QD=QE.
求证:点Q在∠AOB的平分线上.
这样,我们又可以得到一个结论:
到角两边距离相等的点在角的平分线上。
B
A
D
O
P
E
C
∵
PD⊥OA,PE⊥OB,PD=PE
∴点Q在∠AOB的平分线上.
用几何语言表示:
例
已知:如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
A
B
C
P
M
N
A
B
C
P
M
N
例
已知:如图,△ABC的角平分线BM、CN相交于点P.
求证:点P到三边AB、BC、CA的距离相等.
证明:过点P作PD
、PE、PF分别垂直于AB、
BC、CA,垂足分别为D、E、F
F
D
E
D
E
∵BM是△ABC的角平分线,点P在BM上
∴PD=PE
同理
PE=PF.
∴
PD=PE=PF.
即点P到边AB、BC、
CA的距离相等
想一想,点P在∠A
的
平分线上吗?这说明三角形的三条角平分线有什么关系?
三角形的三条角平分线相交于一点。
例2、如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是点E,F,且BE=CF。
求证:AD是△ABC的角平分线。
A
B
C
E
F
D
练习
教材P98练习1
2
1、如图,求作一点P,使PC=PD,并且点P到∠AOB的两边的距离相等.
C●
D●
A
B
O
拓展与延伸
2、如图,为了促进当地旅游发展,某地要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?
3、直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有:(
)
A.一处
B.
两处
C.三处
D.四处
分析:由于没有限制在何处选址,故要求的地址共有四处。
D
小结:
1:画一个已知角的角平分线;
及画一条已知直线的垂线;
2:角平分线的性质:
角的平分线上的点到角的两边的距离相等.
3:角平分线的判定结论:
到角的两边的距离相等的点在角平分线上。
练习
教材P99习题2,3,4,5
