人教版数学九年级上册24.4 圆的弧长与扇形面积 课件(共20张ppt)
文档属性
| 名称 | 人教版数学九年级上册24.4 圆的弧长与扇形面积 课件(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 06:35:25 | ||
图片预览






文档简介
(共20张PPT)
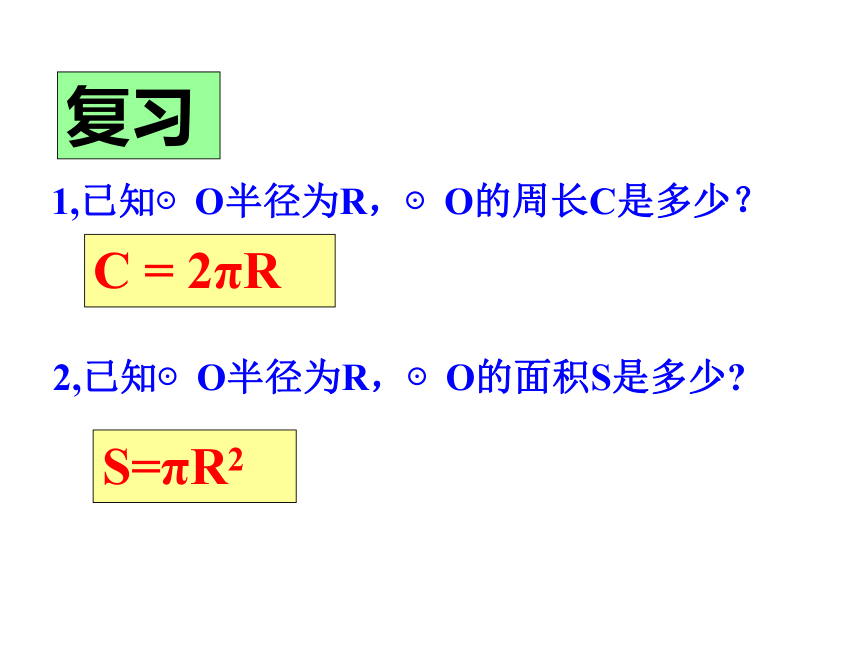
复习
2,已知⊙O半径为R,⊙O的面积S是多少?
S=πR2
C
=
2πR
1,已知⊙O半径为R,⊙O的周长C是多少?
新课引入
1°圆心角所对的弧长是多少?
2°圆心角所对的弧长是多少?
n°呢?
圆的周长可以看作是多少度圆心角所对的弧长?
360°
在半径为R的圆中,n°的圆心角所对的弧长为
(1)n表示1°的圆心角的倍数,它不带单位
(2)公式中L、n、R三个量中已知两量可求第三量.
注意
小组活动
根据弧长的计算公式为
L、n、R三个量中已知两量可求第三量.请
各小组拟出一题写出已知求解过程.
在半径为R的圆中,n°的圆心角所对的弧长为
思考:弧长的大小与哪些量有关?
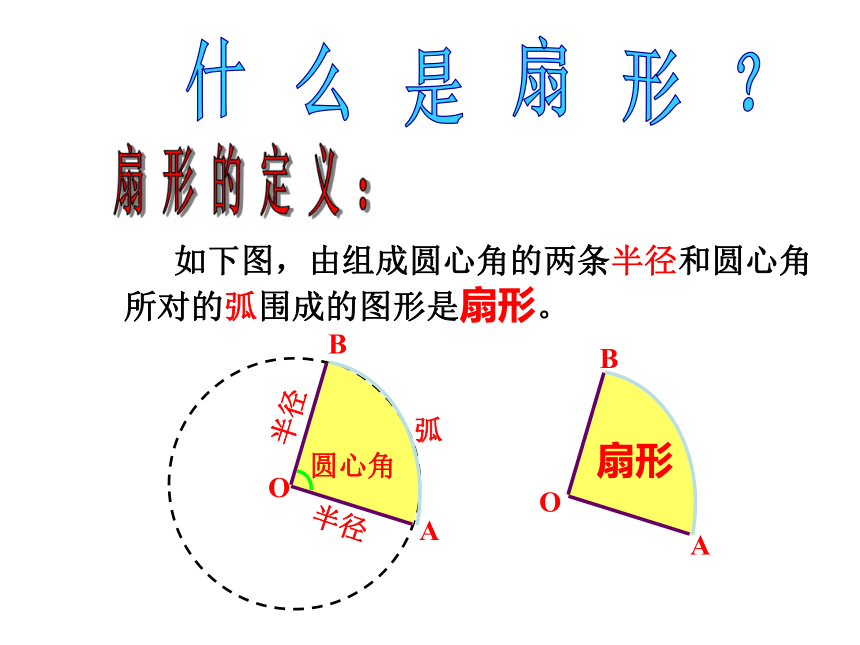
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
在半径为R
的圆中,n°的圆心角所对的扇形面积计算公式为
120o
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的一端拴着一只狗。
如果这只狗拴在夹角为120°的墙角
,那么它的
最大活动区域有多大?这个区域的边缘长是多少?
比较扇形面积(S)公式和弧长(l)公式,你能用弧长来表示扇形的面积吗?
探索弧长与扇形面积的关系
l
R
例1、制造弯形管道时,经常要先按中心线计算“展直长
度”,再下料,试计算图中所示的管道的展直长度
L
(结果取整数).
A
B
C
D
O
R=900
mm
700
mm
700
mm
100°
解:由弧长公式,得AB的长
因此所要求的展直长度
A
B
C
D
O
R=900
mm
700
mm
700
mm
100°
例2、如图,水平放置的圆柱形排水管道的截面半径是
0.6
m,其中水面高
0.3
m,求截面上有水部分的面积(结果保留小数点后两位).
O
A
B
C
D
解:连接OA,OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C,连接AC.
OC=0.6
m,DC=0.3
m,
OD=OC-CD=0.3(m)
OD=DC
又AD
DC
AD是线段OC的垂直平分线
AC=AO=OC
从而
AOD=
AOB=
有水部分的面积
一个概念
三个公式
一种类比
一种转化
1、已知半径为2cm的扇形,其弧长为
,则这个扇形的面积,S扇=
.
2、如果一个扇形面积是它所在圆的面积
的,
则此扇形的圆心角
45°
随堂练习
课后作业
教科书
第1、2、3题
再见
复习
2,已知⊙O半径为R,⊙O的面积S是多少?
S=πR2
C
=
2πR
1,已知⊙O半径为R,⊙O的周长C是多少?
新课引入
1°圆心角所对的弧长是多少?
2°圆心角所对的弧长是多少?
n°呢?
圆的周长可以看作是多少度圆心角所对的弧长?
360°
在半径为R的圆中,n°的圆心角所对的弧长为
(1)n表示1°的圆心角的倍数,它不带单位
(2)公式中L、n、R三个量中已知两量可求第三量.
注意
小组活动
根据弧长的计算公式为
L、n、R三个量中已知两量可求第三量.请
各小组拟出一题写出已知求解过程.
在半径为R的圆中,n°的圆心角所对的弧长为
思考:弧长的大小与哪些量有关?
如下图,由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
在半径为R
的圆中,n°的圆心角所对的扇形面积计算公式为
120o
在一块空旷的草地上有一根柱子,柱子上拴着一条长3m的绳子,绳子的一端拴着一只狗。
如果这只狗拴在夹角为120°的墙角
,那么它的
最大活动区域有多大?这个区域的边缘长是多少?
比较扇形面积(S)公式和弧长(l)公式,你能用弧长来表示扇形的面积吗?
探索弧长与扇形面积的关系
l
R
例1、制造弯形管道时,经常要先按中心线计算“展直长
度”,再下料,试计算图中所示的管道的展直长度
L
(结果取整数).
A
B
C
D
O
R=900
mm
700
mm
700
mm
100°
解:由弧长公式,得AB的长
因此所要求的展直长度
A
B
C
D
O
R=900
mm
700
mm
700
mm
100°
例2、如图,水平放置的圆柱形排水管道的截面半径是
0.6
m,其中水面高
0.3
m,求截面上有水部分的面积(结果保留小数点后两位).
O
A
B
C
D
解:连接OA,OB,作弦AB的垂直平分线,垂足为D,交弧AB于点C,连接AC.
OC=0.6
m,DC=0.3
m,
OD=OC-CD=0.3(m)
OD=DC
又AD
DC
AD是线段OC的垂直平分线
AC=AO=OC
从而
AOD=
AOB=
有水部分的面积
一个概念
三个公式
一种类比
一种转化
1、已知半径为2cm的扇形,其弧长为
,则这个扇形的面积,S扇=
.
2、如果一个扇形面积是它所在圆的面积
的,
则此扇形的圆心角
45°
随堂练习
课后作业
教科书
第1、2、3题
再见
同课章节目录
