人教版数学九年级上册 第24章 24.1圆的有关性质同步测试试题(word解析版)
文档属性
| 名称 | 人教版数学九年级上册 第24章 24.1圆的有关性质同步测试试题(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 437.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 19:16:06 | ||
图片预览


文档简介
圆的有关性质同步测试试题(一)
一.选择题
1.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OB=3:5,连接DO,则DE的长为( )
A.3 B.4 C.6 D.8
2.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则△OFC的面积是( )
A.40cm2 B.20cm2 C.10cm2 D.5cm2
3.如图,在⊙O中,点B是的中点,点D在上,连接OA、OB、BD、CD.若∠AOB=50°,则∠BDC的大小为( )
A.50° B.35° C.25° D.15°
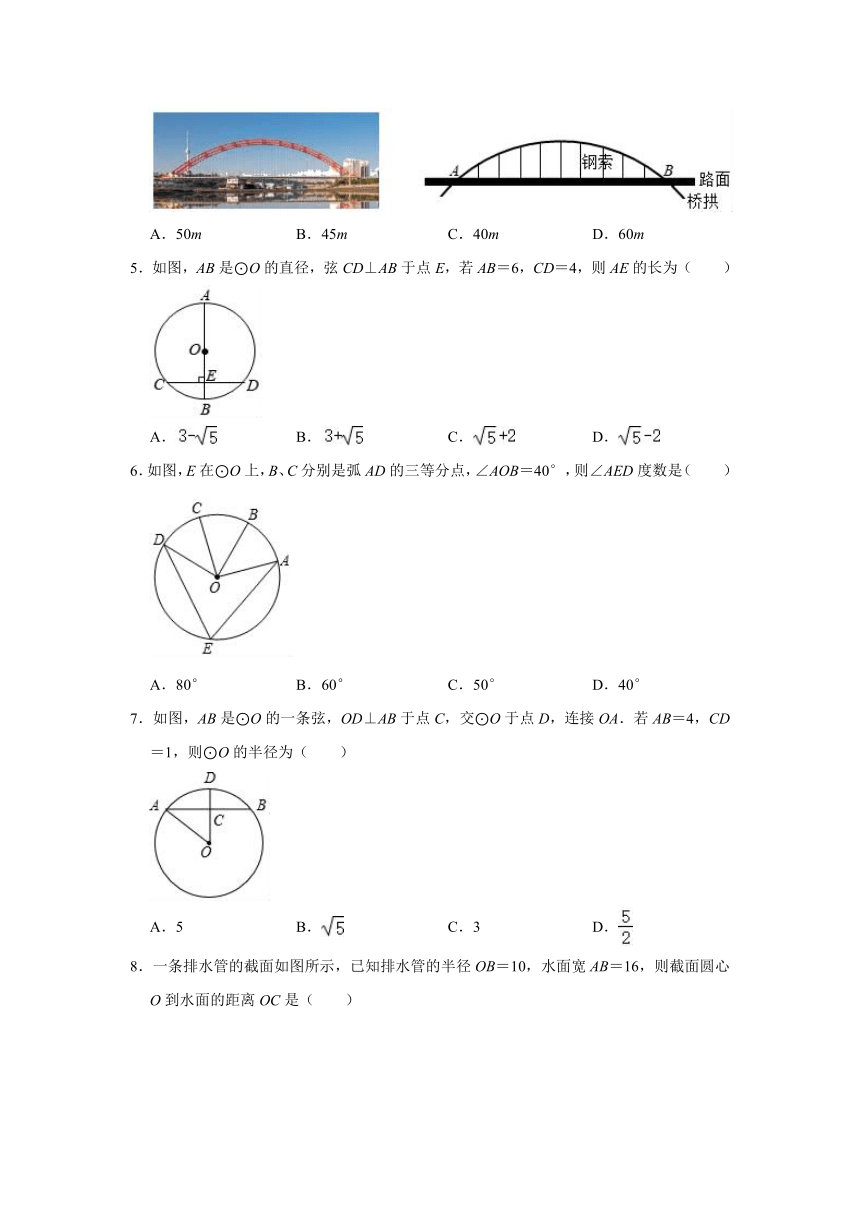
4.如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
A.50m B.45m C.40m D.60m
5.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=6,CD=4,则AE的长为( )
A. B. C. D.
6.如图,E在⊙O上,B、C分别是弧AD的三等分点,∠AOB=40°,则∠AED度数是( )
A.80° B.60° C.50° D.40°
7.如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,连接OA.若AB=4,CD=1,则⊙O的半径为( )
A.5 B. C.3 D.
8.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
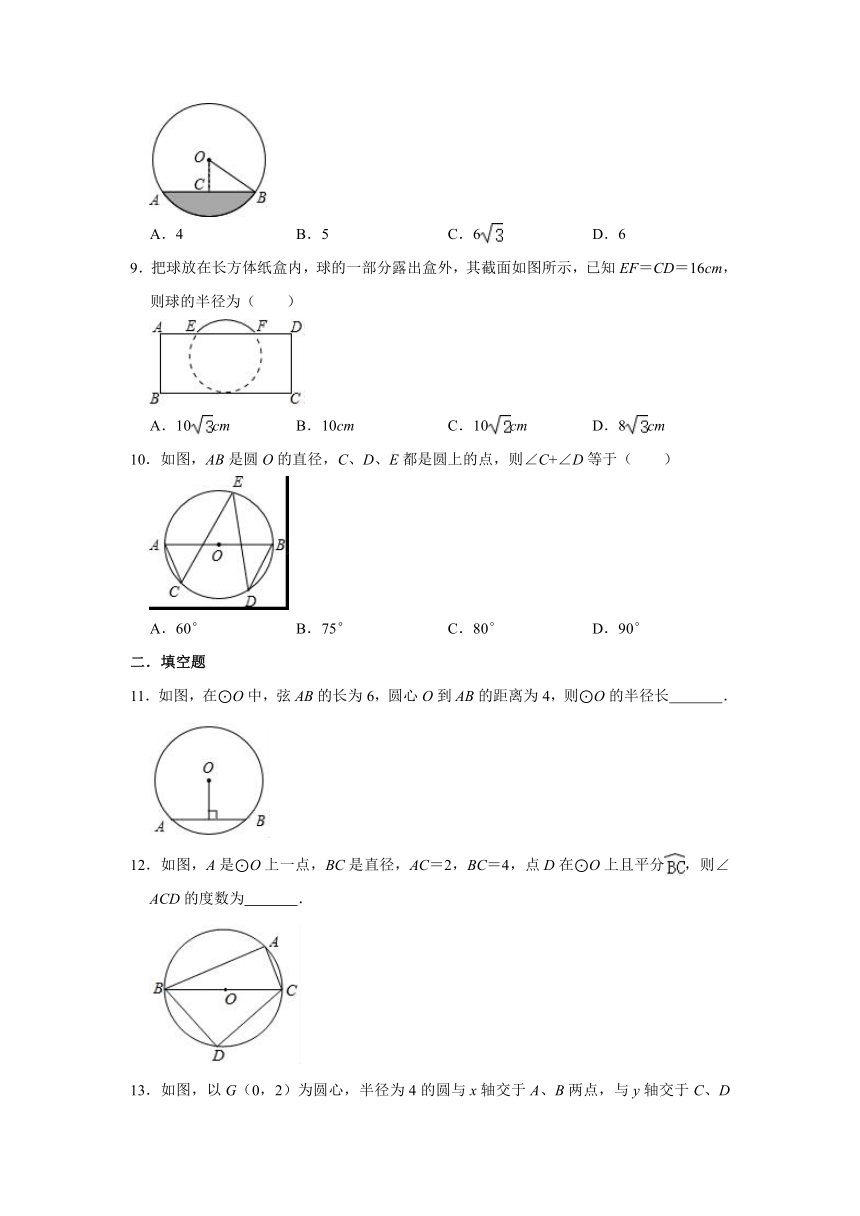
9.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
A.10cm B.10cm C.10cm D.8cm
10.如图,AB是圆O的直径,C、D、E都是圆上的点,则∠C+∠D等于( )
A.60° B.75° C.80° D.90°
二.填空题
11.如图,在⊙O中,弦AB的长为6,圆心O到AB的距离为4,则⊙O的半径长 .
12.如图,A是⊙O上一点,BC是直径,AC=2,BC=4,点D在⊙O上且平分,则∠ACD的度数为 .
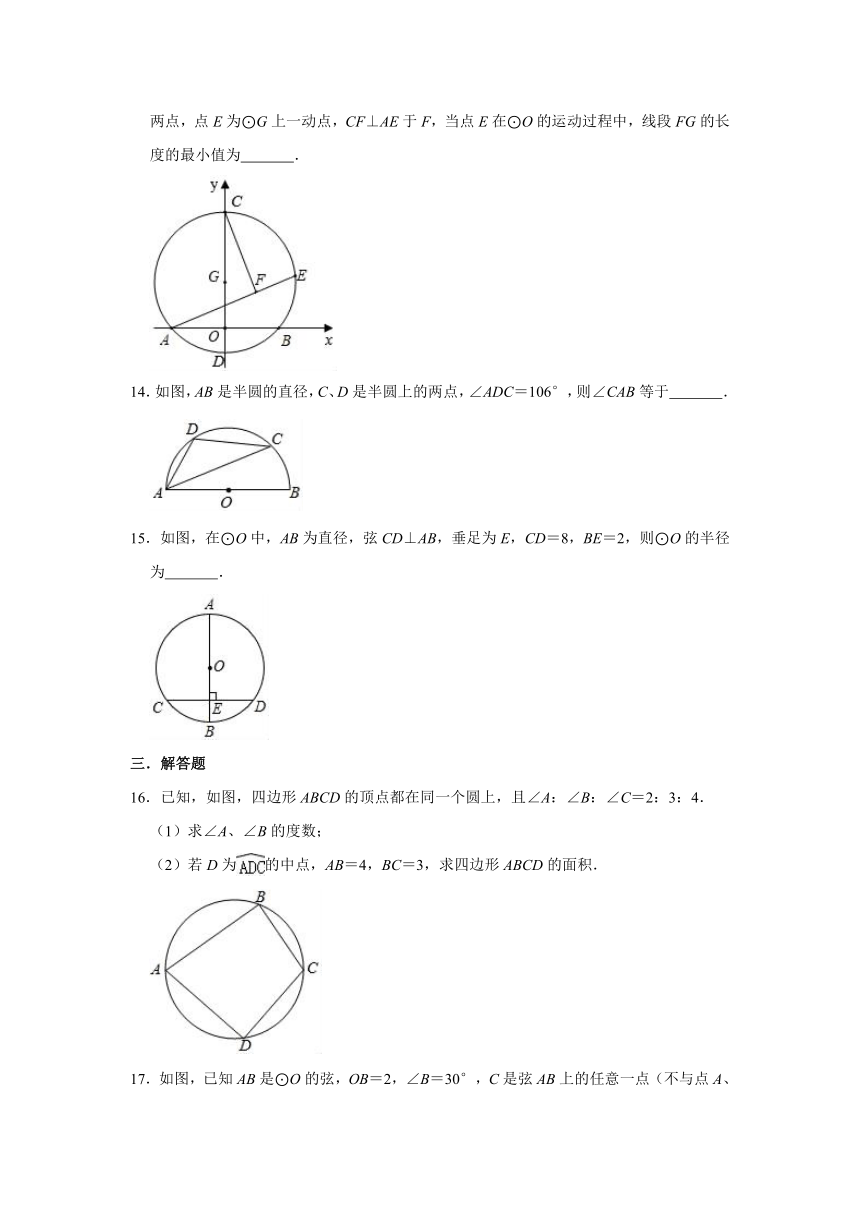
13.如图,以G(0,2)为圆心,半径为4的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E在⊙O的运动过程中,线段FG的长度的最小值为 .
14.如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于 .
15.如图,在⊙O中,AB为直径,弦CD⊥AB,垂足为E,CD=8,BE=2,则⊙O的半径为 .
三.解答题
16.已知,如图,四边形ABCD的顶点都在同一个圆上,且∠A:∠B:∠C=2:3:4.
(1)求∠A、∠B的度数;
(2)若D为的中点,AB=4,BC=3,求四边形ABCD的面积.
17.如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)求弦AB的长;
(2)当∠D=20°时,求∠BOD的度数.
18.已知:⊙O的半径为25cm,弦AB=40cm,弦CD=48cm,AB∥CD.求这两条平行弦AB,CD之间的距离.
19.如图,在平面直角坐标系中,以点M(0,)为圆心,以长为半径作⊙M交x轴于A、B两点,交y轴于C、D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
(1)求点C、P的坐标;
(2)求证:BE=2OE.
参考答案与试题解析
一.选择题
1.【解答】解:∵AB=10,OC:OB=3:5,
∴OC=3,
在Rt△OCD中,CD===4,
∵DE⊥AB,
∴DE=2CD=8,
故选:D.
2.【解答】解:连接OB,如图所示:
设⊙O的半径为rcm,则OE=(r﹣2)cm,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,
∴BE=DE=4(cm),
在Rt△OBE中,∵OE2+BE2=OB2 ,
∴(r﹣2)2+42=r2
解得:r=5,
∴AC=10(cm),EC=AC﹣AE=8(cm),
∴BC===4(cm),
∵OF⊥BC,
∴CF=BF=BC=2(cm),
∴OF===(cm),
∴△OFC的面积=CF×OF=×2×=5(cm2),
故选:D.
3.【解答】解:连接OC,如图,
∵点B是的中点,
∴=,
∴∠AOB=∠BOC=50°,
∵∠BDC=∠BOC=25°.
故选:C.
4.【解答】解:设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,如图所示:
则OA=OD=250,AC=BC=AB=150,
∴OC===200,
∴CD=OD﹣OC=250﹣200=50(m),
即这些钢索中最长的一根为50m,
故选:A.
5.【解答】解:连接OC,如图,
∵CD⊥AB,
∴CE=DE=CD=2,
在Rt△OCE中,∵OC=3,CE=2,
∴OE==,
∴AE=OA+OE=3+.
故选:B.
6.【解答】解:∵B、C分别是弧AD的三等分点,
∴==,
∴∠COD=∠BOC=∠AOB=40°,
∴∠AOD=3×40°=120°,
∴∠AED=∠AOD=60°,
故选:B.
7.【解答】解:设⊙O的半径为r,则OA=r,OC=r﹣1,
∵OD⊥AB,AB=4,
∴AC=AB=2,
在Rt△ACO中,OA2=AC2+OC2,
∴r2=22+(r﹣1)2,
r=,
故选:D.
8.【解答】解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:D.
9.【解答】解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
设OF=x,则OM=16﹣x,MF=8,
在直角三角形OMF中,OM2+MF2=OF2,
即:(16﹣x)2+82=x2,
解得:x=10.
故选:B.
10.【解答】解:连接OE,
根据圆周角定理可知:
∠C=∠AOE,∠D=∠BOE,
则∠C+∠D=(∠AOE+∠BOE)=90°,
故选:D.
二.填空题(共5小题)
11.【解答】解:连接OA,如图所示:
由题意得:OC⊥AB,OC=4,
∴AC=BC=AB=3,
在Rt△OAC中,∵OC=4,AC=3,
∴OA===5,
即⊙O的半径为5.
故答案为:5.
12.【解答】解:∵BC是⊙O的直径,
∴∠BAC=∠D=90°,
∵AC=2,AB=4,
∴cos∠ACB==,
∴∠ACB=60°,
又∵点D在⊙O上且平分,
∴,
∴BD=CD,
∴△BCD是等腰直角三角形,
∴∠DCB=∠DBC=45°,
∴∠ACD=∠ACB+∠DCB=105°,
故答案为:105°.
13.【解答】解:过G作GM⊥AC于M,连接AG,如图所示:
∵GO⊥AB,
∴OA=OB,
∵G(0,2),
∴OG=2,
在Rt△AGO中,∵AG=4,OG=2,
∴AG=2OG,OA==2,
∴∠GAO=30°,AB=2AO=4,
∴∠AGO=60°,
∵GC=GA=4,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=4,MG=CG=2,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣MG=2﹣2,
故答案为:2﹣2.
14.【解答】解:连接BD,如图,所示:
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠BDC=∠ADC﹣∠ADB=106°﹣90°=16°,
∴∠CAB=∠BDC=16°.
故答案为:16°.
15.【解答】解:连接OC,如图所示:
∵CD⊥AB,
∴CE=DE=CD=4,
设⊙O的半径为r,则OE=r﹣2,OC=r,
在Rt△OCE中,由勾股定理得:42+(r﹣2)2=r2,
解得:r=5,
即⊙O的半径为5.
故答案为:5.
三.解答题(共4小题)
16.【解答】解:(1)设∠A、∠B、∠C分别为2x、3x、4x,
∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,即2x+4x=180°,
解得,x=30°,
∴∠A、∠B分别为60°、90°;
(2)连接AC,
∵∠B=90°,
∴AC为圆的直径,AC==5,△ABC的面积=×3×4=6,∠D=90°,
∵点D为的中点,
∴AD=CD=AC=,
∴△ADC的面积=××=,
∴四边形ABCD的面积=6+=.
17.【解答】解:(1)过点O作OE⊥AB于E,如图:
则AE=BE=AB,∠OEB=90°,
∵OB=2,∠B=30°,
∴OE=OB=1,BE=OE=,
∴AB=2BE=2;
(2)连接OA,如图:
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D,
又∵∠B=30°,∠D=20°,
∴∠DAB=50°,
∴∠BOD=2∠DAB=100°.
18.【解答】解:(1)如图1,连接OB,OD,做OM⊥AB交CD于点N,
∵AB∥CD,
∴ON⊥CD,
∵AB=40cm,CD=48cm,
∴BM=20cm,DN=24cm,
∵⊙O的半径为25cm,
∴OB=OD=25cm,
∴OM=15cm,ON=7cm,
∵MN=OM﹣ON,
∴MN=8cm,
(2)如图2,连接OB,OD,做直线OM⊥AB交CD于点N,
∵AB∥CD,
∴ON⊥CD,
∵AB=40cm,CD=48cm,
∴BM=20cm,DN=24cm,
∵⊙O的半径为25cm,
∴OB=OD=25cm,
∴OM=15cm,ON=7cm,
∵MN=OM+ON,
∴MN=22cm.
∴平行弦AB,CD之间的距离为8cm或22cm.
19.【解答】(1)解:连接PB,∵PA是圆M的直径,∴∠PBA=90°
∴AO=OB=3
又∵MO⊥AB,∴PB∥MO.∴PB=2OM=
∴P点坐标为(3,)(2分)
在直角三角形ABP中,AB=6,PB=2,
根据勾股定理得:AP=4,
所以圆的半径MC=2,又OM=,
所以OC=MC﹣OM=,
则C(0,)(1分)
(2)证明:连接AC.
∵AM=MC=2,AO=3,OC=,
∴AM=MC=AC=2,
∴△AMC为等边三角形(2分)
又∵AP为圆M的直径
得∠ACP=90
一.选择题
1.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OB=3:5,连接DO,则DE的长为( )
A.3 B.4 C.6 D.8
2.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则△OFC的面积是( )
A.40cm2 B.20cm2 C.10cm2 D.5cm2
3.如图,在⊙O中,点B是的中点,点D在上,连接OA、OB、BD、CD.若∠AOB=50°,则∠BDC的大小为( )
A.50° B.35° C.25° D.15°
4.如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
A.50m B.45m C.40m D.60m
5.如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=6,CD=4,则AE的长为( )
A. B. C. D.
6.如图,E在⊙O上,B、C分别是弧AD的三等分点,∠AOB=40°,则∠AED度数是( )
A.80° B.60° C.50° D.40°
7.如图,AB是⊙O的一条弦,OD⊥AB于点C,交⊙O于点D,连接OA.若AB=4,CD=1,则⊙O的半径为( )
A.5 B. C.3 D.
8.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.6
9.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
A.10cm B.10cm C.10cm D.8cm
10.如图,AB是圆O的直径,C、D、E都是圆上的点,则∠C+∠D等于( )
A.60° B.75° C.80° D.90°
二.填空题
11.如图,在⊙O中,弦AB的长为6,圆心O到AB的距离为4,则⊙O的半径长 .
12.如图,A是⊙O上一点,BC是直径,AC=2,BC=4,点D在⊙O上且平分,则∠ACD的度数为 .
13.如图,以G(0,2)为圆心,半径为4的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E在⊙O的运动过程中,线段FG的长度的最小值为 .
14.如图,AB是半圆的直径,C、D是半圆上的两点,∠ADC=106°,则∠CAB等于 .
15.如图,在⊙O中,AB为直径,弦CD⊥AB,垂足为E,CD=8,BE=2,则⊙O的半径为 .
三.解答题
16.已知,如图,四边形ABCD的顶点都在同一个圆上,且∠A:∠B:∠C=2:3:4.
(1)求∠A、∠B的度数;
(2)若D为的中点,AB=4,BC=3,求四边形ABCD的面积.
17.如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)求弦AB的长;
(2)当∠D=20°时,求∠BOD的度数.
18.已知:⊙O的半径为25cm,弦AB=40cm,弦CD=48cm,AB∥CD.求这两条平行弦AB,CD之间的距离.
19.如图,在平面直角坐标系中,以点M(0,)为圆心,以长为半径作⊙M交x轴于A、B两点,交y轴于C、D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
(1)求点C、P的坐标;
(2)求证:BE=2OE.
参考答案与试题解析
一.选择题
1.【解答】解:∵AB=10,OC:OB=3:5,
∴OC=3,
在Rt△OCD中,CD===4,
∵DE⊥AB,
∴DE=2CD=8,
故选:D.
2.【解答】解:连接OB,如图所示:
设⊙O的半径为rcm,则OE=(r﹣2)cm,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,
∴BE=DE=4(cm),
在Rt△OBE中,∵OE2+BE2=OB2 ,
∴(r﹣2)2+42=r2
解得:r=5,
∴AC=10(cm),EC=AC﹣AE=8(cm),
∴BC===4(cm),
∵OF⊥BC,
∴CF=BF=BC=2(cm),
∴OF===(cm),
∴△OFC的面积=CF×OF=×2×=5(cm2),
故选:D.
3.【解答】解:连接OC,如图,
∵点B是的中点,
∴=,
∴∠AOB=∠BOC=50°,
∵∠BDC=∠BOC=25°.
故选:C.
4.【解答】解:设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,如图所示:
则OA=OD=250,AC=BC=AB=150,
∴OC===200,
∴CD=OD﹣OC=250﹣200=50(m),
即这些钢索中最长的一根为50m,
故选:A.
5.【解答】解:连接OC,如图,
∵CD⊥AB,
∴CE=DE=CD=2,
在Rt△OCE中,∵OC=3,CE=2,
∴OE==,
∴AE=OA+OE=3+.
故选:B.
6.【解答】解:∵B、C分别是弧AD的三等分点,
∴==,
∴∠COD=∠BOC=∠AOB=40°,
∴∠AOD=3×40°=120°,
∴∠AED=∠AOD=60°,
故选:B.
7.【解答】解:设⊙O的半径为r,则OA=r,OC=r﹣1,
∵OD⊥AB,AB=4,
∴AC=AB=2,
在Rt△ACO中,OA2=AC2+OC2,
∴r2=22+(r﹣1)2,
r=,
故选:D.
8.【解答】解:∵OC⊥AB,OC过圆心O点,
∴BC=AC=AB=×16=8,
在Rt△OCB中,由勾股定理得:OC===6,
故选:D.
9.【解答】解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
设OF=x,则OM=16﹣x,MF=8,
在直角三角形OMF中,OM2+MF2=OF2,
即:(16﹣x)2+82=x2,
解得:x=10.
故选:B.
10.【解答】解:连接OE,
根据圆周角定理可知:
∠C=∠AOE,∠D=∠BOE,
则∠C+∠D=(∠AOE+∠BOE)=90°,
故选:D.
二.填空题(共5小题)
11.【解答】解:连接OA,如图所示:
由题意得:OC⊥AB,OC=4,
∴AC=BC=AB=3,
在Rt△OAC中,∵OC=4,AC=3,
∴OA===5,
即⊙O的半径为5.
故答案为:5.
12.【解答】解:∵BC是⊙O的直径,
∴∠BAC=∠D=90°,
∵AC=2,AB=4,
∴cos∠ACB==,
∴∠ACB=60°,
又∵点D在⊙O上且平分,
∴,
∴BD=CD,
∴△BCD是等腰直角三角形,
∴∠DCB=∠DBC=45°,
∴∠ACD=∠ACB+∠DCB=105°,
故答案为:105°.
13.【解答】解:过G作GM⊥AC于M,连接AG,如图所示:
∵GO⊥AB,
∴OA=OB,
∵G(0,2),
∴OG=2,
在Rt△AGO中,∵AG=4,OG=2,
∴AG=2OG,OA==2,
∴∠GAO=30°,AB=2AO=4,
∴∠AGO=60°,
∵GC=GA=4,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=4,MG=CG=2,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣MG=2﹣2,
故答案为:2﹣2.
14.【解答】解:连接BD,如图,所示:
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠BDC=∠ADC﹣∠ADB=106°﹣90°=16°,
∴∠CAB=∠BDC=16°.
故答案为:16°.
15.【解答】解:连接OC,如图所示:
∵CD⊥AB,
∴CE=DE=CD=4,
设⊙O的半径为r,则OE=r﹣2,OC=r,
在Rt△OCE中,由勾股定理得:42+(r﹣2)2=r2,
解得:r=5,
即⊙O的半径为5.
故答案为:5.
三.解答题(共4小题)
16.【解答】解:(1)设∠A、∠B、∠C分别为2x、3x、4x,
∵四边形ABCD为圆内接四边形,
∴∠A+∠C=180°,即2x+4x=180°,
解得,x=30°,
∴∠A、∠B分别为60°、90°;
(2)连接AC,
∵∠B=90°,
∴AC为圆的直径,AC==5,△ABC的面积=×3×4=6,∠D=90°,
∵点D为的中点,
∴AD=CD=AC=,
∴△ADC的面积=××=,
∴四边形ABCD的面积=6+=.
17.【解答】解:(1)过点O作OE⊥AB于E,如图:
则AE=BE=AB,∠OEB=90°,
∵OB=2,∠B=30°,
∴OE=OB=1,BE=OE=,
∴AB=2BE=2;
(2)连接OA,如图:
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D,
又∵∠B=30°,∠D=20°,
∴∠DAB=50°,
∴∠BOD=2∠DAB=100°.
18.【解答】解:(1)如图1,连接OB,OD,做OM⊥AB交CD于点N,
∵AB∥CD,
∴ON⊥CD,
∵AB=40cm,CD=48cm,
∴BM=20cm,DN=24cm,
∵⊙O的半径为25cm,
∴OB=OD=25cm,
∴OM=15cm,ON=7cm,
∵MN=OM﹣ON,
∴MN=8cm,
(2)如图2,连接OB,OD,做直线OM⊥AB交CD于点N,
∵AB∥CD,
∴ON⊥CD,
∵AB=40cm,CD=48cm,
∴BM=20cm,DN=24cm,
∵⊙O的半径为25cm,
∴OB=OD=25cm,
∴OM=15cm,ON=7cm,
∵MN=OM+ON,
∴MN=22cm.
∴平行弦AB,CD之间的距离为8cm或22cm.
19.【解答】(1)解:连接PB,∵PA是圆M的直径,∴∠PBA=90°
∴AO=OB=3
又∵MO⊥AB,∴PB∥MO.∴PB=2OM=
∴P点坐标为(3,)(2分)
在直角三角形ABP中,AB=6,PB=2,
根据勾股定理得:AP=4,
所以圆的半径MC=2,又OM=,
所以OC=MC﹣OM=,
则C(0,)(1分)
(2)证明:连接AC.
∵AM=MC=2,AO=3,OC=,
∴AM=MC=AC=2,
∴△AMC为等边三角形(2分)
又∵AP为圆M的直径
得∠ACP=90
同课章节目录
