人教版 八年级数学 14.3 因式分解 培优训练(word含答案)
文档属性
| 名称 | 人教版 八年级数学 14.3 因式分解 培优训练(word含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 388.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 19:28:49 | ||
图片预览


文档简介
人教版
八年级数学
14.3
因式分解
培优训练
一、选择题(本大题共10道小题)
1.
(2020?丽水)下列多项式中,能运用平方差公式分解因式的是( )
A.a2+b2
B.2a﹣b2
C.a2﹣b2
D.﹣a2﹣b2
2.
多项式4y2-12y+9因式分解的结果为( )
A.(y-3)2
B.(2y-3)2
C.(y+3)2
D.(2y-9)2
3.
2019·晋州期末
把下列各式分解因式,结果为(x-2y)(x+2y)的多项式是( )
A.x2-4y2
B.x2+4y2
C.-x2+4y2
D.-x2-4y2
4.
多项式6a3b2-3a2b3因式分解时,应提取的公因式为( )
A.3a2b2
B.3a3b2
C.3a2b3
D.3a3b3
5.
将3a2m-6amn+3a分解因式,下面是四位同学分解的结果:
①3am(a-2n+1);②3a(am+2mn-1);③3a(am-2mn);④3a(am-2mn+1).
其中正确的是( )
A.①
B.②
C.③
D.④
6.
如图,长、宽分别为a,b的长方形的周长为10,面积为6,则a2b+ab2的值为( )
A.15
B.30
C.60
D.78
7.
2019·天水秦安期中
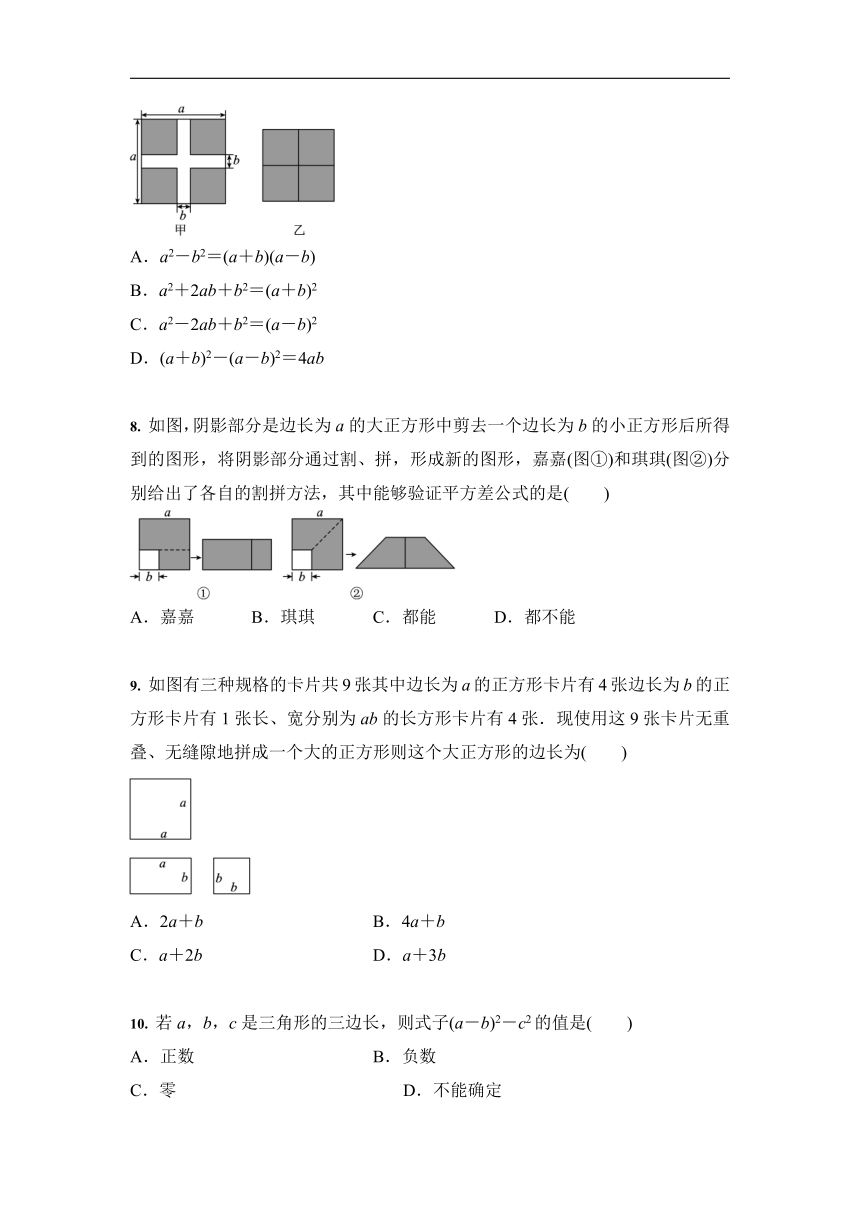
如图将甲图中阴影部分无重叠、无缝隙地拼成乙图根据两个图形中阴影部分的面积关系得到的等式是( )
A.a2-b2=(a+b)(a-b)
B.a2+2ab+b2=(a+b)2
C.a2-2ab+b2=(a-b)2
D.(a+b)2-(a-b)2=4ab
8.
如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,嘉嘉(图①)和琪琪(图②)分别给出了各自的割拼方法,其中能够验证平方差公式的是( )
A.嘉嘉
B.琪琪
C.都能
D.都不能
9.
如图有三种规格的卡片共9张其中边长为a的正方形卡片有4张边长为b的正方形卡片有1张长、宽分别为ab的长方形卡片有4张.现使用这9张卡片无重叠、无缝隙地拼成一个大的正方形则这个大正方形的边长为( )
A.2a+b
B.4a+b
C.a+2b
D.a+3b
10.
若a,b,c是三角形的三边长,则式子(a-b)2-c2的值是( )
A.正数
B.负数
C.零
D.不能确定
二、填空题(本大题共6道小题)
11.
(2020·株洲)因式分解:________.
12.
(2020·安徽)分解因式:ab2-a
=
.
13.
(2020·天水)分解因式:m3n-mn=________.
14.
2018·成都已知x+y=0.2x+3y=1则式子x2+4xy+4y2的值为________.
15.
若a-b=3x-y=2则a2-2ab+b2-x+y=________.
16.
(2020·常德)阅读理解:对于这类特殊的代数式可以按下面的方法分解因式:.
理解运用:如果,那么,即有或,因此,方程和的所有解就是方程的解.
解决问题:求方程的解为______.
三、解答题(本大题共4道小题)
17.
如图,在一块边长为a的正方形纸板的四个角上各剪去一个边长为b(b<)的小正方形,做一个无盖长方体纸盒,长方体纸盒所用的纸板(图中阴影部分)的面积是多少?当a=22.4,b=7.7时,这个面积的值又是多少?请利用分解因式的方法计算.
18.
分解因式:;
19.
分解因式:
20.
证明:在都是大于l的整数时,是合数.
人教版
八年级数学
14.3
因式分解
培优训练-答案
一、选择题(本大题共10道小题)
1.
【答案】C
【解析】能运用平方差公式因式分解的两项都是平方的形式或能化成平方的形式且两项必须是符号相反,只有a2﹣b2同时满足这两个条件,所以本题选C.
2.
【答案】B [解析]
4y2-12y+9=(2y)2-2×2y×3+32=(2y-3)2.
3.
【答案】A
4.
【答案】A
5.
【答案】D
6.
【答案】B [解析]
根据题意,得a+b=5,ab=6,则a2b+ab2=ab(a+b)=30.
7.
【答案】C [解析]
甲图中阴影部分的面积为a2-2ab+b2图乙中阴影部分的面积为(a-b)2
所以a2-2ab+b2=(a-b)2.
8.
【答案】C [解析]
在图①中,阴影部分的面积相等,左边的图形阴影部分的面积=a2-b2,右边的图形阴影部分的面积=(a+b)(a-b),故可得a2-b2=(a+b)(a-b),可以验证平方差公式;
在图②中,阴影部分的面积相等,左边的图形阴影部分的面积=a2-b2,右边的图形阴影部分的面积=(2b+2a)·(a-b)=(a+b)(a-b),故可得a2-b2=(a+b)(a-b),可以验证平方差公式.
9.
【答案】A [解析]
由题可知9张卡片的总面积为4a2+4ab+b2.因为4a2+4ab+b2=(2a+b)2所以大正方形的边长为2a+b.
10.
【答案】B [解析]
因为(a-b)2-c2=(a-b+c)(a-b-c),且a,b,c是三角形的三边长,
所以a+c-b>0,a-b-c<0.
所以(a-b)2-c2的值是负数.
故选B.
二、填空题(本大题共6道小题)
11.
【答案】
【解析】运用提公因式法分解因式即可.
.
故答案为:
12.
【答案】
a(b+1)(b-1)
【解析】原式=a(b2-1)=a(b+1)(b-1).
13.
【答案】mn(m+1)(m-1)
【解析】先提公因式,再利用平方差公式继续分解因式,m3n-mn=mn(m2-1)=mn(m+1)(m-1).
14.
【答案】0.36 [解析]
因为x+y=0.2x+3y=1所以2x+4y=1.2即x+2y=0.6.则原式=(x+2y)2=0.36.
15.
【答案】7 [解析]
a2-2ab+b2-x+y=(a-b)2-(x-y).
把a-b=3x-y=2代入得原式=32-2=7.
16.
【答案】或或
【解析】本题考查了因式分解的应用,因式分解是研究代数式的基础,通过因式分解将多项式合理变形,是求代数式值的常用解题方法,具体做法是:根据题目的特点,先通过因式分解将式子变形,然后再进行整体代入.解:,,,
,则,即,
或,解得或.因此本题答案为:或或.
三、解答题(本大题共4道小题)
17.
【答案】
解:长方体纸盒所用的纸板(图中阴影部分)的面积为a2-4b2.
当a=22.4,b=7.7时,
原式=(a+2b)(a-2b)
=(22.4+15.4)(22.4-15.4)
=37.8×7
=264.6.
18.
【答案】
【解析】;
19.
【答案】
【解析】
20.
【答案】
由于在都大于1时,两个因数中较小的那一个
即两个因数都是的真因数,所以是合数.
八年级数学
14.3
因式分解
培优训练
一、选择题(本大题共10道小题)
1.
(2020?丽水)下列多项式中,能运用平方差公式分解因式的是( )
A.a2+b2
B.2a﹣b2
C.a2﹣b2
D.﹣a2﹣b2
2.
多项式4y2-12y+9因式分解的结果为( )
A.(y-3)2
B.(2y-3)2
C.(y+3)2
D.(2y-9)2
3.
2019·晋州期末
把下列各式分解因式,结果为(x-2y)(x+2y)的多项式是( )
A.x2-4y2
B.x2+4y2
C.-x2+4y2
D.-x2-4y2
4.
多项式6a3b2-3a2b3因式分解时,应提取的公因式为( )
A.3a2b2
B.3a3b2
C.3a2b3
D.3a3b3
5.
将3a2m-6amn+3a分解因式,下面是四位同学分解的结果:
①3am(a-2n+1);②3a(am+2mn-1);③3a(am-2mn);④3a(am-2mn+1).
其中正确的是( )
A.①
B.②
C.③
D.④
6.
如图,长、宽分别为a,b的长方形的周长为10,面积为6,则a2b+ab2的值为( )
A.15
B.30
C.60
D.78
7.
2019·天水秦安期中
如图将甲图中阴影部分无重叠、无缝隙地拼成乙图根据两个图形中阴影部分的面积关系得到的等式是( )
A.a2-b2=(a+b)(a-b)
B.a2+2ab+b2=(a+b)2
C.a2-2ab+b2=(a-b)2
D.(a+b)2-(a-b)2=4ab
8.
如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,嘉嘉(图①)和琪琪(图②)分别给出了各自的割拼方法,其中能够验证平方差公式的是( )
A.嘉嘉
B.琪琪
C.都能
D.都不能
9.
如图有三种规格的卡片共9张其中边长为a的正方形卡片有4张边长为b的正方形卡片有1张长、宽分别为ab的长方形卡片有4张.现使用这9张卡片无重叠、无缝隙地拼成一个大的正方形则这个大正方形的边长为( )
A.2a+b
B.4a+b
C.a+2b
D.a+3b
10.
若a,b,c是三角形的三边长,则式子(a-b)2-c2的值是( )
A.正数
B.负数
C.零
D.不能确定
二、填空题(本大题共6道小题)
11.
(2020·株洲)因式分解:________.
12.
(2020·安徽)分解因式:ab2-a
=
.
13.
(2020·天水)分解因式:m3n-mn=________.
14.
2018·成都已知x+y=0.2x+3y=1则式子x2+4xy+4y2的值为________.
15.
若a-b=3x-y=2则a2-2ab+b2-x+y=________.
16.
(2020·常德)阅读理解:对于这类特殊的代数式可以按下面的方法分解因式:.
理解运用:如果,那么,即有或,因此,方程和的所有解就是方程的解.
解决问题:求方程的解为______.
三、解答题(本大题共4道小题)
17.
如图,在一块边长为a的正方形纸板的四个角上各剪去一个边长为b(b<)的小正方形,做一个无盖长方体纸盒,长方体纸盒所用的纸板(图中阴影部分)的面积是多少?当a=22.4,b=7.7时,这个面积的值又是多少?请利用分解因式的方法计算.
18.
分解因式:;
19.
分解因式:
20.
证明:在都是大于l的整数时,是合数.
人教版
八年级数学
14.3
因式分解
培优训练-答案
一、选择题(本大题共10道小题)
1.
【答案】C
【解析】能运用平方差公式因式分解的两项都是平方的形式或能化成平方的形式且两项必须是符号相反,只有a2﹣b2同时满足这两个条件,所以本题选C.
2.
【答案】B [解析]
4y2-12y+9=(2y)2-2×2y×3+32=(2y-3)2.
3.
【答案】A
4.
【答案】A
5.
【答案】D
6.
【答案】B [解析]
根据题意,得a+b=5,ab=6,则a2b+ab2=ab(a+b)=30.
7.
【答案】C [解析]
甲图中阴影部分的面积为a2-2ab+b2图乙中阴影部分的面积为(a-b)2
所以a2-2ab+b2=(a-b)2.
8.
【答案】C [解析]
在图①中,阴影部分的面积相等,左边的图形阴影部分的面积=a2-b2,右边的图形阴影部分的面积=(a+b)(a-b),故可得a2-b2=(a+b)(a-b),可以验证平方差公式;
在图②中,阴影部分的面积相等,左边的图形阴影部分的面积=a2-b2,右边的图形阴影部分的面积=(2b+2a)·(a-b)=(a+b)(a-b),故可得a2-b2=(a+b)(a-b),可以验证平方差公式.
9.
【答案】A [解析]
由题可知9张卡片的总面积为4a2+4ab+b2.因为4a2+4ab+b2=(2a+b)2所以大正方形的边长为2a+b.
10.
【答案】B [解析]
因为(a-b)2-c2=(a-b+c)(a-b-c),且a,b,c是三角形的三边长,
所以a+c-b>0,a-b-c<0.
所以(a-b)2-c2的值是负数.
故选B.
二、填空题(本大题共6道小题)
11.
【答案】
【解析】运用提公因式法分解因式即可.
.
故答案为:
12.
【答案】
a(b+1)(b-1)
【解析】原式=a(b2-1)=a(b+1)(b-1).
13.
【答案】mn(m+1)(m-1)
【解析】先提公因式,再利用平方差公式继续分解因式,m3n-mn=mn(m2-1)=mn(m+1)(m-1).
14.
【答案】0.36 [解析]
因为x+y=0.2x+3y=1所以2x+4y=1.2即x+2y=0.6.则原式=(x+2y)2=0.36.
15.
【答案】7 [解析]
a2-2ab+b2-x+y=(a-b)2-(x-y).
把a-b=3x-y=2代入得原式=32-2=7.
16.
【答案】或或
【解析】本题考查了因式分解的应用,因式分解是研究代数式的基础,通过因式分解将多项式合理变形,是求代数式值的常用解题方法,具体做法是:根据题目的特点,先通过因式分解将式子变形,然后再进行整体代入.解:,,,
,则,即,
或,解得或.因此本题答案为:或或.
三、解答题(本大题共4道小题)
17.
【答案】
解:长方体纸盒所用的纸板(图中阴影部分)的面积为a2-4b2.
当a=22.4,b=7.7时,
原式=(a+2b)(a-2b)
=(22.4+15.4)(22.4-15.4)
=37.8×7
=264.6.
18.
【答案】
【解析】;
19.
【答案】
【解析】
20.
【答案】
由于在都大于1时,两个因数中较小的那一个
即两个因数都是的真因数,所以是合数.
