人教版数学七年级上册 第4单元4.1---4.4复习题(word版含答案)
文档属性
| 名称 | 人教版数学七年级上册 第4单元4.1---4.4复习题(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 677.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览

文档简介
人教版数学七年级上册
第4章
4.1---4.4复习题含答案
4.1几何图形
一.选择题
1.用一个平面去截一个圆柱体,截面图形不可能是( )
A.长方形
B.梯形
C.圆形
D.椭圆形
2.如图是正方体的展开图,则原正方体相对两个面上的数字和最小是( )
A.8
B.7
C.6
D.4
3.如图,是一个五棱柱形的几何体,下列关于该几何体的叙述正确的是( )
A.有4条侧棱
B.有5个面
C.有10条棱
D.有10个顶点
4.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )
A.
B.
C.
D.
5.如图的正方体纸巾盒,它的平面展开图是( )
A.
B.
C.
D.
6.下列叙述,其中正确的个数有( )
①最小的正整数是0;
②若x+2是一个负数,则x一定是负数;
③用一个平面去裁正方体,截面不可能是六边形;
④三角形是多边形;
⑤绝对值等于本身的数是正整数.
A.1
B.2
C.3
D.4
7.如图所示的纸片折成一个长方体纸盒,折得的纸盒是( )
A.
B.
C.
D.
8.如图的平面展开图折叠成正方体后,相对面上的数都互为相反数,那么a的值是( )
A.1
B.﹣2
C.3
D.﹣b
9.如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A.
B.
C.
D.
10.下列图形中,可能是右面正方体的展开图的是( )
A.
B.
C.
D.
二.填空题
11.如果一个棱柱共有15条棱,那么它一定是
棱柱.
12.设三棱柱有a个面,b条棱,c个顶点,则a﹣b﹣c=
.
13.国际奥委会会旗上的图案是由代表五大洲的五个圆环组成,现在在某体育馆前的草坪上要修剪出此图案.已知,每个圆环的内、外半径分别为4米和5米,图中重叠部分的每个小曲边四边形的面积都为1平方米,若修剪每平方米的人工费用为10元,则修剪此图案所花费的人工费为
元(π取3).
14.如图,阴影部分的面积为
cm2.(π取3.14)
15.如图,两个长方形重叠部分的面积相当于大长方形面积的,相当于小长方形面积的,则大长方形和小长方形的面积的比值是
.
三.解答题
16.有一个硬纸做成的礼品盒,用彩带扎住(如图),打结处用去的彩带长18厘米.
(1)共需要彩带多少厘米?
(2)做这样一个礼品盒至少要多少硬纸?
(3)这个礼品盒的体积是多少?(π取3.14)
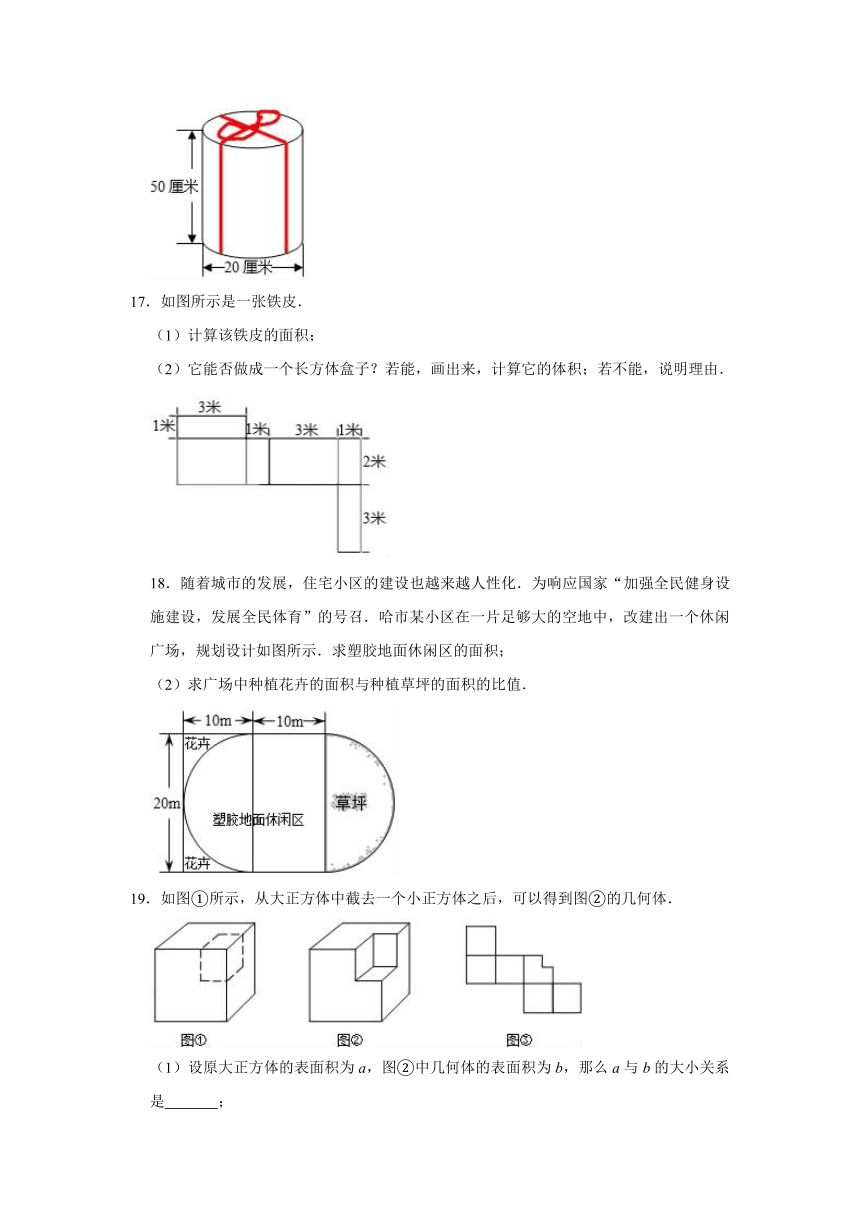
17.如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)它能否做成一个长方体盒子?若能,画出来,计算它的体积;若不能,说明理由.
18.随着城市的发展,住宅小区的建设也越来越人性化.为响应国家“加强全民健身设施建设,发展全民体育”的号召.哈市某小区在一片足够大的空地中,改建出一个休闲广场,规划设计如图所示.求塑胶地面休闲区的面积;
(2)求广场中种植花卉的面积与种植草坪的面积的比值.
19.如图①所示,从大正方体中截去一个小正方体之后,可以得到图②的几何体.
(1)设原大正方体的表面积为a,图②中几何体的表面积为b,那么a与b的大小关系是
;
A.a>b;B.a<b;C.a=b;D.无法判断.
(2)小明说“设图①中大正方体的棱长之和为m,图②中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图③是图②几何体的表面展开图吗?如有错误,请予修正.
参考答案与试题解析
一.选择题
1.【解答】解:用一个平面去截一个圆柱体,
截面图形可能是:长方形、正方形,圆形,椭圆形,
但不可能是梯形.
故选:B.
2.【解答】解:易得2和6是相对的两个面;3和4是相对两个面;1和5是相对的两个面,
所以原正方体相对两个面上的数字和最小的是6,
故选:C.
3.【解答】解:图中几何体是正五棱柱,五棱柱有
7个面,10个顶点,5条侧棱,15条棱.
故选:D.
4.【解答】解:A、不能折叠成正方体,故选项错误;
B、不能折成圆锥,故选项错误;
C、能折成圆柱,故选项正确;
D、不能折成三棱柱,故选项错误.
故选:C.
5.【解答】解:观察图形可知,正方体纸巾盒的平面展开图是:
故选:C.
6.【解答】解:①最小的正整数是1,此结论错误;
②若x+2是一个负数,则x一定是负数是正确的;
③用一个平面去截正方体,截面与六个面均相交即可得六边形,此结论错误;
④三角形是多边形是正确的;
⑤绝对值等于本身的数是正数和0,此结论错误.
故正确的个数有2个.
故选:B.
7.【解答】解:如图所示:
根据题意可知,A的对面是A′,B的对面是B′,C的对面是C′,A的短边阴影与C的阴影重合.
故用形如图所示的纸片折成一个长方体纸盒,折得的纸盒是C.
故选:C.
8.【解答】解:“a”与“﹣1”相对,
∵相对面上的两个数都互为相反数,
∴a=1.
故选:A.
9.【解答】解:因圆柱的展开面为长方形,AC展开应该是两线段,且有公共点C.
故选:A.
10.【解答】解:A、折叠后,圆不是与两个空白小正方形相邻,故与原正方体不符,故此选项错误;
B、折叠后,圆与三角形成对面,与原正方体不符,故此选项错误;
C、折叠后与原正方体相同,与原正方体符合,故此选项正确;
D、折叠后,两个三角形的短边不是与两个空白小正方形相邻,与原正方体不符,故此选项错误.
故选:C.
二.填空题(共5小题)
11.【解答】解:15÷3=5,
所以是五棱柱,
故答案为:五.
12.【解答】解:三棱柱有5个面,9条棱,6个顶点,
因此a=5,b=9,c=6,
所以a﹣b﹣c=5﹣9﹣6=﹣10,
故答案为:﹣10.
13.【解答】解:修剪草坪的面积为:(π×52﹣π×42)×5﹣1×8=45π﹣8≈127(平方米),
因此所用的人工费为10×127=1270(元),
故答案为:1270.
14.【解答】解:S阴影=S圆形﹣S正方形=π×()2﹣×2×2=π﹣2≈1.14(cm2),
故答案为:1.14.
15.【解答】解:设阴影部分的面积为k,
∵阴影部分的面积相当于大长方形面积的,相当于小长方形面积的,
∴大长方形的面积为6k,小长方形的面积为4k,
∴大长方形和小长方形的面积的比值为=,
故答案为:.
三.解答题(共4小题)
16.【解答】解:(1)50×4+20×4+18=298(cm),
(2)π×()2×2+π×20×50=200π+1000π=1200π(cm2),
(3)π×()2×50=5000π≈15700(cm3),
答:做这样一个礼品盒共需要彩带298厘米;至少要1200π平方厘米的硬纸;这个礼品盒的体积约为15700立方厘米.
17.【解答】解:(1)(1×3+2×3+1×2)×2=22(m2),
(2)根据棱柱的展开与折叠,可得可以折叠成长方体的盒子,其长、宽、高分别为3cm,2cm,1cm,
因此体积为:1×2×3=6(m3),
18.【解答】解:(1)S塑胶地面=S长方形+S半圆=10×20+π×()2=200+50π≈350(平方米),
答:塑胶地面休闲区的面积为350平方米;
(2)S种花卉=S长方形﹣S半圆=200﹣150=50(平方米),
S种草坪=S半圆=50π≈150(平方米),
所以,广场中种植花卉的面积与种植草坪的面积的比值为=.
19.【解答】解:(1)根据“切去三个小面”但又“新增三个小面”,因此与原来的表面积相等,即a=b,
故答案为:C;
(2)如图②红颜色的棱是多出来的,共6条,
如果截去的小正方体的棱长为大正方体的棱长的一半时,n比m正好多出大正方体的3条棱的长度,
如果截去的小正方体的棱长不是大正方体的棱长的一半,n比m就不是多出大正方体的
4.2直线、射线、线段
一.选择题
1.平面上有不同的三个点,经过其中任意两点画直线,一共可以画( )
A.1条
B.2条
C.3条
D.1条或3条
2.下列说法正确的是( )
A.延长直线AB到点C
B.延长射线AB到点C
C.延长线段AB到点C
D.射线AB与射线BA是同一条射线
3.平面上有三点A、B、C,如果AB=10,AC=7,BC=3,那么( )
A.点C在线段AB上
B.点C在线段AB的延长线上
C.点C在直线AB外
D.点C可能在直线AB上,也可能在直线AB外
4.如图,在公路MN两侧分别有A1,A2…A7,七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
①车站的位置设在C点好于B点;
②车站的位置设在B点与C点之间公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关;
④车站的位置设在BC段公路的最中间处要好于设在点B及点C处.
A.①③
B.③④
C.②③
D.②
5.图中共有线段( )
A.4条
B.6条
C.8条
D.10条
6.现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”,请用数学知识解释图中这一现象,其原因( )
A.两点之间,线段最短
B.过一点有无数条直线
C.两点确定一条直线
D.两点之间线段的长度,叫做这两点之间的距离
7.有下列生活、生产现象:
①从A地到B地架设电线,总是尽可能沿着线段AB架设.
②用两个钉子就可以把木条固定在墙上.
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线.
④把弯曲的公路改直,就能缩短路程.
其中能用“两点之间,线段最短”来解释的现象有( )
A.①④
B.②④
C.①②
D.③④
8.下列四个说法中,正确的有( )个
(1)﹣24=(﹣2)4;
(2)﹣|﹣1|=﹣(﹣1)3
(3)若a+1与b﹣1互为相反数,则2a+2b=0;
(4)若线段AB=BC,则点B是线段AC的中点.
A.1
B.2
C.3
D.4
9.在下列生活、生产现象中,不可以用基本事实“两点确定一条直线”来解释的有( )
A.用两颗钉子就可以把木条固定在墙上
B.当木工师傅锯木板时,他会用墨盒在木板上弹出墨线,这样会使木板沿直线锯下
C.把弯曲的公路改直,就能缩短路程
D.在正常情况下,射击时只要保证瞄准的一只眼在两个准星确定的直线上,就能射中目标
10.某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.线段的定义
D.圆弧的定义
二.填空题
11.西成高铁是中国首条穿越秦岭的高速铁路,大大减少了人们从西安到四川成都的时间,实现了人们“早上游大雁塔,晚上逛宽窄巷”的美好愿望.建造直隧道的目的可以用数学知识解释为
.
12.如图,点A,B是直线l上的两点,点C,D在直线l上且点C在点D的左侧,点D在点B的右侧.AC:CB=1:2,BD:AB=2:3.若CD=12,则AB=
.
13.海南环岛高铁是世界首创,其中某趟列车在东段的三亚站、陵水站、万宁站、琼海站、文昌站和海口东站6个站之间运行,那么该趟列车需要安排不同的车票
种,票价
种.
14.如图,把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是
.
15.如图,C为射线AB上一点,AB=30,AC比BC的多5,P、Q两点分别从A、B两点同时出发,分别以2个单位/秒和1个单位/秒的速度在射线AB上沿AB方向运动,当点P运动到点B时,两点同时停止运动,运动时间为t(s),M为BP的中点,N为MQ的中点,以下结论:①BC=2AC;②AB=4NQ;③当BP=BQ时,t=12;④M,N两点之间的距离是定值.其中正确的结论
(填写序号)
三.解答题
16.已知:点M是直线AB上的点,线段AB=12,AM=2,点N是线段MB的中点,画出图形并求线段MN的长.
17.如图,已知点C在线段AB上,点M,N分别在线段AC与线段BC上,且AM=2MC,BN=2NC.
(1)若AC=9,BC=6,求线段MN的长;
(2)若MN=5,求线段AB的长.
18.如图:A、B、C、D四点在同一直线上.
(1)若AB=CD.
①比较线段的大小:AC
BD(填“>”、“=”或“<”);
②若BC=AC,且AC=12cm,则AD的长为
cm;
(2)若线段AD被点B、C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是16cm,求AD的长.
19.如图,已知线段AB=4,延长AB到点C,使得AB=2BC,反向延长AB到点D,使AC=2AD.
(1)求线段CD的长;
(2)若Q为AB的中点,P为线段CD上一点,且BP=BC,求线段PQ的长.
参考答案与试题解析
一.选择题
1.【解答】解:如图,经过其中任意两点画直线可以画3条直线或1条直线,
故选:D.
2.【解答】解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
3.【解答】解:如图,在平面内,AB=10,
∵AC=7,BC=3,
∴点C为以A为圆心,7为半径,与以B为圆心,3为半径的两个圆的交点,
由于AB=10=7+3=AC+BC,
所以,点C在线段AB上,
故选:A.
4.【解答】解:①通过测量发现车站的位置设在C点好于B点,故原来的结论正确;
②车站设在B点与C点之间公路上,车站朝M方向始终有4个工厂,车站朝N方向始终有3个工厂,所以在这一段任何一点,效果一样,故原来的结论错误;
③工厂到车站的距离是线段的长,和各段的弯曲的小公路无关,故原来的结论正确;
④车站的位置设在BC段公路的最中间处与设在点B及点C处一样好,故原来的结论错误.
故选:A.
5.【解答】解:图中的线段有AC、AD、AE、AB;CD、CE、CB;DE、DB;EB;共10条,
故选:D.
6.【解答】解:现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”,请用数学知识解释图中这一现象,
其原因是两点之间,线段最短,
故选:A.
7.【解答】解:根据两点之间,线段最短,得到的是:①④;
②③的依据是两点确定一条直线.
故选:A.
8.【解答】解:(1)﹣24=﹣16,(﹣2)4=16
所以(1)错误;
(2)﹣|﹣1|=﹣1
﹣(﹣1)3=1
所以(2)错误;
(3)∵a+1与b﹣1互为相反数,
∴a+1+b﹣1=0
∴a+b=0
则2a+2b=0
所以(3)正确;
(4)线段AB=BC,如果点A、B、C三个点不在同一条直线上,
则点B不是线段AC的中点.
所以(4)错误.
所以正确的有1个.
故选:A.
9.【解答】解:A、用两颗钉子就可以把木条固定在墙上,可以用基本事实“两点确定一条直线”来解释,故本选项不符合题意.
B、当木工师傅锯木板时,他会用墨盒在木板上弹出墨线,这样会使木板沿直线锯下,可以用基本事实“两点确定一条直线”来解释,故本选项不符合题意.
C、把弯曲的公路改直,就能缩短路程,可以用基本事实“两点之间,线段最短”来解释,不能用基本事实“两点确定一条直线”来解释,故本选项符合题意.
D、在正常情况下,射击时只要保证瞄准的一只眼在两个准星确定的直线上,就能射中目标可以用基本事实“两点确定一条直线”来解释,故本选项不符合题意.
故选:C.
10.【解答】解:剩下的银杏叶的周长比原银杏叶的周长要小根据是两点之间线段最短,
故选:A.
二.填空题(共5小题)
11.【解答】解:建造直隧道的目的可以用数学知识解释为:两点之间,线段最短.
故答案为:两点之间,线段最短.
12.【解答】解:对C点的位置分情况讨论如下:
①C点在A点的左边,
∵AC:CB=1:2,BD:AB=2:3,
假设AC=3k,
则AB=3k,BD=2k,
∴CD=3k+3k+2k=8k,
∵CD=12,
∴k=1.5,
∴AB=4.5;
②C点在线段AB上,
∵AC:CB=1:2,BD:AB=2:3,
假设AC=k,
则CB=2k,BD=2k,
∴CD=CB+BD=4k,
∵CD=12,
∴k=3,
∴AB=AC+CB=3k=9;
③C点在B点后,不符合题意,舍去;
∴综上所述,AB=4.5或9.
13.【解答】解:令6个站分别为A、B、C、D、E、F,
则可得所组成的线段有15条,即需要安排15×2=30种不同的车票.
故答案为:30、15.
14.【解答】解:把原来弯曲的河道改直,两地间的河道长度会变短,
这其中蕴含的数学道理是两点之间线段最短.
故答案为:两点之间线段最短.
15.【解答】解:∵AB=30,AC比BC的多5,
∴BC=20,AC=10,
∴BC=2AC;故①正确;
∵P,Q两点分别从A,B两点同时出发,分别以2个单位/秒和1个单位/秒的速度,
∴BP=30﹣2t,BQ=t,
∵M为BP的中点,N为MQ的中点,
∴PM=BP=15﹣t,NQ=MB+BQ=15,NQ=MQ=7.5,
∴AB=4NQ;故②正确;
∵,
∴,解得:t=12,故③正确,
∵BP=30﹣2t,BQ=t,
∴BM=PB=15﹣t,
∴MQ=BM+BQ=15﹣t+t=15,
∴MN=MQ=,
∴MN的值与t无关是定值,
故答案为:①②③④.
三.解答题(共4小题)
16.【解答】解:由于点M的位置不确定,所以需要分类讨论:
①点M在点A左侧,如图1:
∵AB=12,AM=2,
∴MB=AB+AM=12+2=14,
∵N是MB的中点(已知),
∴MN=MB(中点定义),
∵MB=14,
∴MN=×14=7;
②点M在点A右侧,如图2:
∵AB=12,AM=2,
∴MB=AB﹣AM=12﹣2=10,
∵N是MB的中点(已知),
∴MN=MB(中点定义),
∵MB=10,
∴MN=×10=5,
综上所述,MN的长度为5或7.
17.【解答】解:(1)如图,AC=9,BC=6,则AB=AC=BC=9+6=15,
∵AM=2MC,BN=2NC.
∴MC=AC,NC=BC,
∴MN=MC+NC=(AC+BC)=AB=×15=5,
答:MN的长为5;
(2)由(1)得,MN═AB,
若MN=5时,AB=15,
答:AB的长为15.
18.【解答】解:(1)①∵AB=CD,
∴AB+BC=CD+BC,
即,AC=BD,
故答案为:=;
②∵BC=AC,且AC=12cm,
∴BC=×12=9(cm),
∴AB=CD=AC﹣BC=12﹣9=3(cm),
∴AD=AC+CD=12+3=15(cm),
故答案为:15;
(2)如图,
设每份为x,则AB=3x,BC=4x,CD=5x,AD=12x,
∵M是AB的中点,点N是CD的中点N,
∴AM=BM=x,CN=DN=x,
又∵MN=16,
∴x+4x+x=16,
解得,x=2,
∴AD=12x=24(cm),
答:AD的长为24cm.
19.【解答】解:(1)∵AB=4,AB=2BC,
∴BC=2,
∴AC=AB+BC=6,
∵AC=2AD,
∴AD=3,
∴CD=AC+AD=6+3=9;
(2)∵Q为AB中点,
∴BQ=AB=2,
∵BP=BC
4.4角同步
一.选择题
1.上午10:00时,钟表的时针与分针的夹角为( )
A.30°
B.60°
C.90°
D.120°
2.下列说法:①一个角的补角大于这个角;②小于平角的角是钝角;③同角或等角的余角相等;④若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角,其中正确的说法有( )
A.4个
B.3个
C.2个
D.1个
3.已知∠A=115°,∠B是∠A的补角,则∠B的余角的度数是( )
A.65°
B.115°
C.15°
D.25°
4.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=160°,则∠BOC等于( )
A.20°
B.30°
C.40°
D.50°
5.如图,两个直角∠AOC和∠BOD有公共顶点O,下列结论:
①∠AOB=∠COD;
②∠AOB+∠COD=90°;
③若OB平分∠AOC,则OC平分∠BOD;
④∠AOD的平分线与∠BOC的平分线是同一条射线.
其中结论正确的个数是( )
A.4个
B.3个
C.2个
D.1个
6.如图用一副三角板可以画出15°的角,用它们还可以画出其它一些特殊角,不能利用这副三角板直接画出的角度是( )
A.55°
B.75°
C.105°
D.135°
7.下面图形中,射线OP是表示北偏东30°方向的是( )
A.
B.
C.
D.
8.下列说法错误的是( )
A.如果两个角是同一个角的余角,那么这两个角相等
B.任何有理数都可以用数轴上的点表示
C.绝对值等于它的相反数的数都是负数
D.若a=b,则
9.“V”字手势表达胜利,必胜的意义.它源自于英国,“V”为英文Victory(胜利)的首字母.现在“V“字手势早已成为世界用语了.如图的“V”字手势中,食指和中指所夹锐角α的度数为( )
A.25°
B.35°
C.45°
D.55°
10.岛A和岛B处于东西方向的一条直线上,由岛A、岛B分别测得船C位于北偏东40°和北偏西50°方向上,下列符合条件的示意图是( )
A.
B.
C.
D.
二.填空题
11.若两个角互补,且度数之比为3:2,求较大角度数为
.
12.计算:已知∠α=20°20′,则∠α的余角为
.
13.如图,点A在点B的北偏西30°方向,点C在点B的南偏东60°方向.则∠ABC的度数是
.
14.如图,将长方形纸片进行折叠,ED,EF为折痕,A与A'、B与B'、C与C'重合,若∠AED=25°,则∠BEF的度数为
.
15.如图,射线OA的方向是北偏东20度,射线OB的方向是北偏西40度,OD是OB的反向延长线.若OC是∠AOD的平分线,则射线OC的方向是北偏东
度.
三.解答题
16.如图,已知∠ABP与∠CBP互余,∠CBD=32°,BP平分∠ABD.求∠ABP的度数.
17.如图,点O是直线AB上的一点,∠COD是一个直角,OE平分∠BOC.
(1)如图1,当∠AOC=30°,求∠DOE的度数;
(2)如图2,若∠AOC=x°,求∠DOE的度数.(用含有x的代数式表示)
18.如图,已知∠AOC:∠AOB=2:7,OD是∠AOB的平分线,若∠COD=15°,求∠AOC的度数.
19.探究题:如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=100°,将一直角三角形的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?说明理由;
(2)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为
(直接写出结果)
参考答案与试题解析
一.选择题
1.【解答】解:∵10点整,时针指向10,分针指向12,中间相差两大格,
钟表12个数字,每相邻两个数字之间的夹角为30°,
∴10点整分针与时针的夹角是2×30°=60度.
故选:B.
2.【解答】解:①已知∠A=140°,则∠A的补角=40°,原来的说法错误;
②大于直角小于平角的角是钝角,原来的说法错误;
③同角或等角的余角相等是正确的;
④和为180度的两个角互为补角,原来的说法错误.
故其中正确的说法有1个.
故选:D.
3.【解答】解:∠A的补角∠B的度数是:180°﹣115°=65°,
则余角是90°﹣65°=25°.
故选:D.
4.【解答】解:∵∠AOB=∠COD=90°,∠AOD=160°
∴∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣160°=20°.
故选:A.
5.【解答】解:①∵∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠BOC+∠COD=90°,
∴∠AOB=∠COD;
②∠AOB+∠COD=90°不一定和是90°;
③若OB平分∠AOC,则∠AOB=∠BOC=45°,
∴∠COD=45°,
∴OC平分∠BOD;
④∵∠AOB=∠COD,
∴∠BOE=∠COE,
∴∠AOE=∠DOE,
∴∠AOD的平分线与∠BOC的平分线是同一条射线.
∴①③④正确,
故选:B.
6.【解答】解:因为一副三角板有30°、45°、60°、90°的角,
又∵45°﹣30°=15°,45°+30°=75°,
45°+60°=105°,45°+90°=135°.
所以用一副三角板可以画出75°、105°、135°等特殊的角.
故选:A.
7.【解答】解:∵方向角是以正北,正南方向为基准,来描述物体所处的方向,
∴射线OP是表示北偏东30°方向可表示为如图.
故选:D.
8.【解答】解:A.如果两个角是同一个角的余角,那么这两个角相等,说法正确;
B.任何有理数都可以用数轴上的点表示,说法正确;
C.绝对值等于它的相反数的数都是负数和0,故原说法错误;
D.若a=b,则,说法正确;
故选:C.
9.【解答】解:如图所示:食指和中指所夹锐角α的度数为:35°.
故选:B.
10.【解答】解:符合题意的示意图为:
.
故选:D.
二.填空题(共5小题)
11.【解答】解:因为两个角的度数之比为3:2,
所以设这两个角的度数分别为(3x)°和(2x)°.
根据题意,列方程,得3x+2x=180,
解这个方程,得x=36,
所以3x=108.
即较大角度数为108°.
故答案为108°.
12.【解答】解:∠α的余角=90°﹣20°20′=69°40′.
故答案为:69°40′.
13.【解答】解:如图:
由题意,得
∠ABD=30°,∠EBC=60°.
∴∠FBC=90°﹣∠EBC=90°﹣60°=30°.
∵∠DBF=90°,
∴∠ABC=∠ABD+∠DBF+∠FBC=30°+90°+30°=150°,
故答案为:150°.
14.【解答】解:根据翻折的性质可知,∠AED=∠A′ED,∠BEF=∠FEB′,
∵∠AED+∠A′ED+∠BEF+∠FEB′=180°,
∴∠AED+∠BEF=90°,
又∵∠AED=25°,
∴∠BEF=65°.
故答案为:65°.
15.【解答】解:∵OB的方向是北偏西40°,OA的方向是北偏东20°,
∴∠AOB=40°+20°=60°,
∴∠AOD=180°﹣60°=120°,
∵OC是∠AOD的平分线,
∴∠AOC=60°,
∵20°+60°=80°,
∴射线OC的方向是北偏东80°;
故答案为:80.
三.解答题(共4小题)
16.【解答】解:∵∠ABP与∠CBP互余,
∴∠ABP+∠CBP90°,
即:∠ABC=90°,
∵∠CBD=32°,
∴∠ABD=90°+32°=122°,
∵BP平分∠ABD.
∴∠ABP=∠DBP=∠ABD=×122°=61°.
17.【解答】解:(1)∵∠AOC=30°,
∴∠BOC=180°﹣∠AOC=150°,
又∵OE平分∠BOC,
∴∠BOE=∠COE=∠BOC=75°,
又∵∠COD=90°,
∴∠DOE=∠COD﹣∠COE=15°;
(2)∵∠AOC=x°,
∴∠BOC=180°﹣∠AOC=(180﹣x)°,
又∵OE平分∠BOC
∴∠BOE=∠COE=∠BOC=(180﹣x)°,
又∵∠COD=90°
∴∠DOE=∠COD﹣∠COE=90°﹣(180﹣x)°=x°
18.【解答】解:∵∠AOC:∠AOB=2:7,
∴设∠AOC=2x°,∠AOB=7x°,
∵OD是∠AOB的平分线,
∴∠AOD=∠AOB=3.5x°,
∵∠DOC=15°,
∴3.5x﹣2x=15,
∴x=10,
即∠AOC=2x°=20°.
19.【解答】解:(1)平分,理由:延长NO,在延长线上取一点D,
∵∠MON=90°∴∠MOD=90°
∴∠MOB+∠NOB=90°,
∠MOC+∠COD=90°,
∵∠MOB=∠MOC,
∴∠NOB=∠COD,
∵∠NOB=∠AOD,
∴∠COD=∠AOD,
∴直线NO平分∠AOC;
(2)分两种情况:
①如图2,∵∠BOC=100°
∴∠AOC=80°,
当直线ON恰好平分锐角∠AOC时,∠AOD=∠COD=40°,
∴∠BON=40°,∠BOM=50°,
即逆时针旋转的角度为50°,
由题意得,5°t=50°
解得t=10(s);
②如图3,当NO平分∠AOC时,∠NOA=40°,
∴∠AOM=50°,
即逆时针旋转的角度为:180°+50°=230°
4.4 课题学习 设计制作长方体形状的包装纸盒
一、选择题
1.下列四个平面图形中,不能折叠成无盖的长方体盒子的是
( )
2.图是正方体的一种展开图,如果将其折叠成原来的正方体,那么与边a重合的边是
( )
A.d B.e
C.f D.i
二、非选择题
3.图是某些几何体的展开图,请填出这些几何体的名称.
4.图是一个无盖的长方体纸盒展开图,纸盒的底面积为600
cm2.
求:(1)纸盒的高为多少厘米;
(2)展开图的周长为多少厘米.
图
5.图是一个食品包装盒的展开图.请根据图中所标的尺寸,计算这个食品包装盒的表面积和体积.
6.图是一个食品包装盒的展开图(其中的六边形的六条边相等).
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积.
7.一个正方体的展开图已有一部分(如图),还有一个正方形未画出,现有10个位置可供选择,则放在哪些位置能围成正方体,放在哪些位置不能围成正方体?仔细观察图4-4-7,或许你还要动手做做呢!
放在 可围成正方体,放在 不可以围成正方体(填序号).?
参考答案
一、选择题
1.A
2.A
二、非选择题
3.圆锥 三棱柱 长方体
4.解:(1)设底面长为3x
cm,宽为2x
cm.
根据题意,得2x·3x=600,即x2=100,
解得x=10(负值已舍去).
故纸盒的高为10
cm.
(2)展开图的周长为2×(5×10+4×10)=180(cm).
5.解:这个食品包装盒的表面积为2×b2+4×ab=2b2+4ab.体积为b2×a=ab2.
6.解:(1)这个多面体是六棱柱.
(2)这个多面体的侧面积为6ab.
7.①⑦⑧⑨ ②③④⑤⑥⑩
第4章
4.1---4.4复习题含答案
4.1几何图形
一.选择题
1.用一个平面去截一个圆柱体,截面图形不可能是( )
A.长方形
B.梯形
C.圆形
D.椭圆形
2.如图是正方体的展开图,则原正方体相对两个面上的数字和最小是( )
A.8
B.7
C.6
D.4
3.如图,是一个五棱柱形的几何体,下列关于该几何体的叙述正确的是( )
A.有4条侧棱
B.有5个面
C.有10条棱
D.有10个顶点
4.下列选项中,左边的平面图形能够折成右边封闭的立体图形的是( )
A.
B.
C.
D.
5.如图的正方体纸巾盒,它的平面展开图是( )
A.
B.
C.
D.
6.下列叙述,其中正确的个数有( )
①最小的正整数是0;
②若x+2是一个负数,则x一定是负数;
③用一个平面去裁正方体,截面不可能是六边形;
④三角形是多边形;
⑤绝对值等于本身的数是正整数.
A.1
B.2
C.3
D.4
7.如图所示的纸片折成一个长方体纸盒,折得的纸盒是( )
A.
B.
C.
D.
8.如图的平面展开图折叠成正方体后,相对面上的数都互为相反数,那么a的值是( )
A.1
B.﹣2
C.3
D.﹣b
9.如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
A.
B.
C.
D.
10.下列图形中,可能是右面正方体的展开图的是( )
A.
B.
C.
D.
二.填空题
11.如果一个棱柱共有15条棱,那么它一定是
棱柱.
12.设三棱柱有a个面,b条棱,c个顶点,则a﹣b﹣c=
.
13.国际奥委会会旗上的图案是由代表五大洲的五个圆环组成,现在在某体育馆前的草坪上要修剪出此图案.已知,每个圆环的内、外半径分别为4米和5米,图中重叠部分的每个小曲边四边形的面积都为1平方米,若修剪每平方米的人工费用为10元,则修剪此图案所花费的人工费为
元(π取3).
14.如图,阴影部分的面积为
cm2.(π取3.14)
15.如图,两个长方形重叠部分的面积相当于大长方形面积的,相当于小长方形面积的,则大长方形和小长方形的面积的比值是
.
三.解答题
16.有一个硬纸做成的礼品盒,用彩带扎住(如图),打结处用去的彩带长18厘米.
(1)共需要彩带多少厘米?
(2)做这样一个礼品盒至少要多少硬纸?
(3)这个礼品盒的体积是多少?(π取3.14)
17.如图所示是一张铁皮.
(1)计算该铁皮的面积;
(2)它能否做成一个长方体盒子?若能,画出来,计算它的体积;若不能,说明理由.
18.随着城市的发展,住宅小区的建设也越来越人性化.为响应国家“加强全民健身设施建设,发展全民体育”的号召.哈市某小区在一片足够大的空地中,改建出一个休闲广场,规划设计如图所示.求塑胶地面休闲区的面积;
(2)求广场中种植花卉的面积与种植草坪的面积的比值.
19.如图①所示,从大正方体中截去一个小正方体之后,可以得到图②的几何体.
(1)设原大正方体的表面积为a,图②中几何体的表面积为b,那么a与b的大小关系是
;
A.a>b;B.a<b;C.a=b;D.无法判断.
(2)小明说“设图①中大正方体的棱长之和为m,图②中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图③是图②几何体的表面展开图吗?如有错误,请予修正.
参考答案与试题解析
一.选择题
1.【解答】解:用一个平面去截一个圆柱体,
截面图形可能是:长方形、正方形,圆形,椭圆形,
但不可能是梯形.
故选:B.
2.【解答】解:易得2和6是相对的两个面;3和4是相对两个面;1和5是相对的两个面,
所以原正方体相对两个面上的数字和最小的是6,
故选:C.
3.【解答】解:图中几何体是正五棱柱,五棱柱有
7个面,10个顶点,5条侧棱,15条棱.
故选:D.
4.【解答】解:A、不能折叠成正方体,故选项错误;
B、不能折成圆锥,故选项错误;
C、能折成圆柱,故选项正确;
D、不能折成三棱柱,故选项错误.
故选:C.
5.【解答】解:观察图形可知,正方体纸巾盒的平面展开图是:
故选:C.
6.【解答】解:①最小的正整数是1,此结论错误;
②若x+2是一个负数,则x一定是负数是正确的;
③用一个平面去截正方体,截面与六个面均相交即可得六边形,此结论错误;
④三角形是多边形是正确的;
⑤绝对值等于本身的数是正数和0,此结论错误.
故正确的个数有2个.
故选:B.
7.【解答】解:如图所示:
根据题意可知,A的对面是A′,B的对面是B′,C的对面是C′,A的短边阴影与C的阴影重合.
故用形如图所示的纸片折成一个长方体纸盒,折得的纸盒是C.
故选:C.
8.【解答】解:“a”与“﹣1”相对,
∵相对面上的两个数都互为相反数,
∴a=1.
故选:A.
9.【解答】解:因圆柱的展开面为长方形,AC展开应该是两线段,且有公共点C.
故选:A.
10.【解答】解:A、折叠后,圆不是与两个空白小正方形相邻,故与原正方体不符,故此选项错误;
B、折叠后,圆与三角形成对面,与原正方体不符,故此选项错误;
C、折叠后与原正方体相同,与原正方体符合,故此选项正确;
D、折叠后,两个三角形的短边不是与两个空白小正方形相邻,与原正方体不符,故此选项错误.
故选:C.
二.填空题(共5小题)
11.【解答】解:15÷3=5,
所以是五棱柱,
故答案为:五.
12.【解答】解:三棱柱有5个面,9条棱,6个顶点,
因此a=5,b=9,c=6,
所以a﹣b﹣c=5﹣9﹣6=﹣10,
故答案为:﹣10.
13.【解答】解:修剪草坪的面积为:(π×52﹣π×42)×5﹣1×8=45π﹣8≈127(平方米),
因此所用的人工费为10×127=1270(元),
故答案为:1270.
14.【解答】解:S阴影=S圆形﹣S正方形=π×()2﹣×2×2=π﹣2≈1.14(cm2),
故答案为:1.14.
15.【解答】解:设阴影部分的面积为k,
∵阴影部分的面积相当于大长方形面积的,相当于小长方形面积的,
∴大长方形的面积为6k,小长方形的面积为4k,
∴大长方形和小长方形的面积的比值为=,
故答案为:.
三.解答题(共4小题)
16.【解答】解:(1)50×4+20×4+18=298(cm),
(2)π×()2×2+π×20×50=200π+1000π=1200π(cm2),
(3)π×()2×50=5000π≈15700(cm3),
答:做这样一个礼品盒共需要彩带298厘米;至少要1200π平方厘米的硬纸;这个礼品盒的体积约为15700立方厘米.
17.【解答】解:(1)(1×3+2×3+1×2)×2=22(m2),
(2)根据棱柱的展开与折叠,可得可以折叠成长方体的盒子,其长、宽、高分别为3cm,2cm,1cm,
因此体积为:1×2×3=6(m3),
18.【解答】解:(1)S塑胶地面=S长方形+S半圆=10×20+π×()2=200+50π≈350(平方米),
答:塑胶地面休闲区的面积为350平方米;
(2)S种花卉=S长方形﹣S半圆=200﹣150=50(平方米),
S种草坪=S半圆=50π≈150(平方米),
所以,广场中种植花卉的面积与种植草坪的面积的比值为=.
19.【解答】解:(1)根据“切去三个小面”但又“新增三个小面”,因此与原来的表面积相等,即a=b,
故答案为:C;
(2)如图②红颜色的棱是多出来的,共6条,
如果截去的小正方体的棱长为大正方体的棱长的一半时,n比m正好多出大正方体的3条棱的长度,
如果截去的小正方体的棱长不是大正方体的棱长的一半,n比m就不是多出大正方体的
4.2直线、射线、线段
一.选择题
1.平面上有不同的三个点,经过其中任意两点画直线,一共可以画( )
A.1条
B.2条
C.3条
D.1条或3条
2.下列说法正确的是( )
A.延长直线AB到点C
B.延长射线AB到点C
C.延长线段AB到点C
D.射线AB与射线BA是同一条射线
3.平面上有三点A、B、C,如果AB=10,AC=7,BC=3,那么( )
A.点C在线段AB上
B.点C在线段AB的延长线上
C.点C在直线AB外
D.点C可能在直线AB上,也可能在直线AB外
4.如图,在公路MN两侧分别有A1,A2…A7,七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
①车站的位置设在C点好于B点;
②车站的位置设在B点与C点之间公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关;
④车站的位置设在BC段公路的最中间处要好于设在点B及点C处.
A.①③
B.③④
C.②③
D.②
5.图中共有线段( )
A.4条
B.6条
C.8条
D.10条
6.现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”,请用数学知识解释图中这一现象,其原因( )
A.两点之间,线段最短
B.过一点有无数条直线
C.两点确定一条直线
D.两点之间线段的长度,叫做这两点之间的距离
7.有下列生活、生产现象:
①从A地到B地架设电线,总是尽可能沿着线段AB架设.
②用两个钉子就可以把木条固定在墙上.
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线.
④把弯曲的公路改直,就能缩短路程.
其中能用“两点之间,线段最短”来解释的现象有( )
A.①④
B.②④
C.①②
D.③④
8.下列四个说法中,正确的有( )个
(1)﹣24=(﹣2)4;
(2)﹣|﹣1|=﹣(﹣1)3
(3)若a+1与b﹣1互为相反数,则2a+2b=0;
(4)若线段AB=BC,则点B是线段AC的中点.
A.1
B.2
C.3
D.4
9.在下列生活、生产现象中,不可以用基本事实“两点确定一条直线”来解释的有( )
A.用两颗钉子就可以把木条固定在墙上
B.当木工师傅锯木板时,他会用墨盒在木板上弹出墨线,这样会使木板沿直线锯下
C.把弯曲的公路改直,就能缩短路程
D.在正常情况下,射击时只要保证瞄准的一只眼在两个准星确定的直线上,就能射中目标
10.某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是( )
A.两点之间线段最短
B.两点确定一条直线
C.线段的定义
D.圆弧的定义
二.填空题
11.西成高铁是中国首条穿越秦岭的高速铁路,大大减少了人们从西安到四川成都的时间,实现了人们“早上游大雁塔,晚上逛宽窄巷”的美好愿望.建造直隧道的目的可以用数学知识解释为
.
12.如图,点A,B是直线l上的两点,点C,D在直线l上且点C在点D的左侧,点D在点B的右侧.AC:CB=1:2,BD:AB=2:3.若CD=12,则AB=
.
13.海南环岛高铁是世界首创,其中某趟列车在东段的三亚站、陵水站、万宁站、琼海站、文昌站和海口东站6个站之间运行,那么该趟列车需要安排不同的车票
种,票价
种.
14.如图,把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是
.
15.如图,C为射线AB上一点,AB=30,AC比BC的多5,P、Q两点分别从A、B两点同时出发,分别以2个单位/秒和1个单位/秒的速度在射线AB上沿AB方向运动,当点P运动到点B时,两点同时停止运动,运动时间为t(s),M为BP的中点,N为MQ的中点,以下结论:①BC=2AC;②AB=4NQ;③当BP=BQ时,t=12;④M,N两点之间的距离是定值.其中正确的结论
(填写序号)
三.解答题
16.已知:点M是直线AB上的点,线段AB=12,AM=2,点N是线段MB的中点,画出图形并求线段MN的长.
17.如图,已知点C在线段AB上,点M,N分别在线段AC与线段BC上,且AM=2MC,BN=2NC.
(1)若AC=9,BC=6,求线段MN的长;
(2)若MN=5,求线段AB的长.
18.如图:A、B、C、D四点在同一直线上.
(1)若AB=CD.
①比较线段的大小:AC
BD(填“>”、“=”或“<”);
②若BC=AC,且AC=12cm,则AD的长为
cm;
(2)若线段AD被点B、C分成了3:4:5三部分,且AB的中点M和CD的中点N之间的距离是16cm,求AD的长.
19.如图,已知线段AB=4,延长AB到点C,使得AB=2BC,反向延长AB到点D,使AC=2AD.
(1)求线段CD的长;
(2)若Q为AB的中点,P为线段CD上一点,且BP=BC,求线段PQ的长.
参考答案与试题解析
一.选择题
1.【解答】解:如图,经过其中任意两点画直线可以画3条直线或1条直线,
故选:D.
2.【解答】解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
3.【解答】解:如图,在平面内,AB=10,
∵AC=7,BC=3,
∴点C为以A为圆心,7为半径,与以B为圆心,3为半径的两个圆的交点,
由于AB=10=7+3=AC+BC,
所以,点C在线段AB上,
故选:A.
4.【解答】解:①通过测量发现车站的位置设在C点好于B点,故原来的结论正确;
②车站设在B点与C点之间公路上,车站朝M方向始终有4个工厂,车站朝N方向始终有3个工厂,所以在这一段任何一点,效果一样,故原来的结论错误;
③工厂到车站的距离是线段的长,和各段的弯曲的小公路无关,故原来的结论正确;
④车站的位置设在BC段公路的最中间处与设在点B及点C处一样好,故原来的结论错误.
故选:A.
5.【解答】解:图中的线段有AC、AD、AE、AB;CD、CE、CB;DE、DB;EB;共10条,
故选:D.
6.【解答】解:现实生活中“为何有人乱穿马路,却不愿从天桥或斑马线通过?”,请用数学知识解释图中这一现象,
其原因是两点之间,线段最短,
故选:A.
7.【解答】解:根据两点之间,线段最短,得到的是:①④;
②③的依据是两点确定一条直线.
故选:A.
8.【解答】解:(1)﹣24=﹣16,(﹣2)4=16
所以(1)错误;
(2)﹣|﹣1|=﹣1
﹣(﹣1)3=1
所以(2)错误;
(3)∵a+1与b﹣1互为相反数,
∴a+1+b﹣1=0
∴a+b=0
则2a+2b=0
所以(3)正确;
(4)线段AB=BC,如果点A、B、C三个点不在同一条直线上,
则点B不是线段AC的中点.
所以(4)错误.
所以正确的有1个.
故选:A.
9.【解答】解:A、用两颗钉子就可以把木条固定在墙上,可以用基本事实“两点确定一条直线”来解释,故本选项不符合题意.
B、当木工师傅锯木板时,他会用墨盒在木板上弹出墨线,这样会使木板沿直线锯下,可以用基本事实“两点确定一条直线”来解释,故本选项不符合题意.
C、把弯曲的公路改直,就能缩短路程,可以用基本事实“两点之间,线段最短”来解释,不能用基本事实“两点确定一条直线”来解释,故本选项符合题意.
D、在正常情况下,射击时只要保证瞄准的一只眼在两个准星确定的直线上,就能射中目标可以用基本事实“两点确定一条直线”来解释,故本选项不符合题意.
故选:C.
10.【解答】解:剩下的银杏叶的周长比原银杏叶的周长要小根据是两点之间线段最短,
故选:A.
二.填空题(共5小题)
11.【解答】解:建造直隧道的目的可以用数学知识解释为:两点之间,线段最短.
故答案为:两点之间,线段最短.
12.【解答】解:对C点的位置分情况讨论如下:
①C点在A点的左边,
∵AC:CB=1:2,BD:AB=2:3,
假设AC=3k,
则AB=3k,BD=2k,
∴CD=3k+3k+2k=8k,
∵CD=12,
∴k=1.5,
∴AB=4.5;
②C点在线段AB上,
∵AC:CB=1:2,BD:AB=2:3,
假设AC=k,
则CB=2k,BD=2k,
∴CD=CB+BD=4k,
∵CD=12,
∴k=3,
∴AB=AC+CB=3k=9;
③C点在B点后,不符合题意,舍去;
∴综上所述,AB=4.5或9.
13.【解答】解:令6个站分别为A、B、C、D、E、F,
则可得所组成的线段有15条,即需要安排15×2=30种不同的车票.
故答案为:30、15.
14.【解答】解:把原来弯曲的河道改直,两地间的河道长度会变短,
这其中蕴含的数学道理是两点之间线段最短.
故答案为:两点之间线段最短.
15.【解答】解:∵AB=30,AC比BC的多5,
∴BC=20,AC=10,
∴BC=2AC;故①正确;
∵P,Q两点分别从A,B两点同时出发,分别以2个单位/秒和1个单位/秒的速度,
∴BP=30﹣2t,BQ=t,
∵M为BP的中点,N为MQ的中点,
∴PM=BP=15﹣t,NQ=MB+BQ=15,NQ=MQ=7.5,
∴AB=4NQ;故②正确;
∵,
∴,解得:t=12,故③正确,
∵BP=30﹣2t,BQ=t,
∴BM=PB=15﹣t,
∴MQ=BM+BQ=15﹣t+t=15,
∴MN=MQ=,
∴MN的值与t无关是定值,
故答案为:①②③④.
三.解答题(共4小题)
16.【解答】解:由于点M的位置不确定,所以需要分类讨论:
①点M在点A左侧,如图1:
∵AB=12,AM=2,
∴MB=AB+AM=12+2=14,
∵N是MB的中点(已知),
∴MN=MB(中点定义),
∵MB=14,
∴MN=×14=7;
②点M在点A右侧,如图2:
∵AB=12,AM=2,
∴MB=AB﹣AM=12﹣2=10,
∵N是MB的中点(已知),
∴MN=MB(中点定义),
∵MB=10,
∴MN=×10=5,
综上所述,MN的长度为5或7.
17.【解答】解:(1)如图,AC=9,BC=6,则AB=AC=BC=9+6=15,
∵AM=2MC,BN=2NC.
∴MC=AC,NC=BC,
∴MN=MC+NC=(AC+BC)=AB=×15=5,
答:MN的长为5;
(2)由(1)得,MN═AB,
若MN=5时,AB=15,
答:AB的长为15.
18.【解答】解:(1)①∵AB=CD,
∴AB+BC=CD+BC,
即,AC=BD,
故答案为:=;
②∵BC=AC,且AC=12cm,
∴BC=×12=9(cm),
∴AB=CD=AC﹣BC=12﹣9=3(cm),
∴AD=AC+CD=12+3=15(cm),
故答案为:15;
(2)如图,
设每份为x,则AB=3x,BC=4x,CD=5x,AD=12x,
∵M是AB的中点,点N是CD的中点N,
∴AM=BM=x,CN=DN=x,
又∵MN=16,
∴x+4x+x=16,
解得,x=2,
∴AD=12x=24(cm),
答:AD的长为24cm.
19.【解答】解:(1)∵AB=4,AB=2BC,
∴BC=2,
∴AC=AB+BC=6,
∵AC=2AD,
∴AD=3,
∴CD=AC+AD=6+3=9;
(2)∵Q为AB中点,
∴BQ=AB=2,
∵BP=BC
4.4角同步
一.选择题
1.上午10:00时,钟表的时针与分针的夹角为( )
A.30°
B.60°
C.90°
D.120°
2.下列说法:①一个角的补角大于这个角;②小于平角的角是钝角;③同角或等角的余角相等;④若∠1+∠2+∠3=180°,则∠1、∠2、∠3互为补角,其中正确的说法有( )
A.4个
B.3个
C.2个
D.1个
3.已知∠A=115°,∠B是∠A的补角,则∠B的余角的度数是( )
A.65°
B.115°
C.15°
D.25°
4.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=160°,则∠BOC等于( )
A.20°
B.30°
C.40°
D.50°
5.如图,两个直角∠AOC和∠BOD有公共顶点O,下列结论:
①∠AOB=∠COD;
②∠AOB+∠COD=90°;
③若OB平分∠AOC,则OC平分∠BOD;
④∠AOD的平分线与∠BOC的平分线是同一条射线.
其中结论正确的个数是( )
A.4个
B.3个
C.2个
D.1个
6.如图用一副三角板可以画出15°的角,用它们还可以画出其它一些特殊角,不能利用这副三角板直接画出的角度是( )
A.55°
B.75°
C.105°
D.135°
7.下面图形中,射线OP是表示北偏东30°方向的是( )
A.
B.
C.
D.
8.下列说法错误的是( )
A.如果两个角是同一个角的余角,那么这两个角相等
B.任何有理数都可以用数轴上的点表示
C.绝对值等于它的相反数的数都是负数
D.若a=b,则
9.“V”字手势表达胜利,必胜的意义.它源自于英国,“V”为英文Victory(胜利)的首字母.现在“V“字手势早已成为世界用语了.如图的“V”字手势中,食指和中指所夹锐角α的度数为( )
A.25°
B.35°
C.45°
D.55°
10.岛A和岛B处于东西方向的一条直线上,由岛A、岛B分别测得船C位于北偏东40°和北偏西50°方向上,下列符合条件的示意图是( )
A.
B.
C.
D.
二.填空题
11.若两个角互补,且度数之比为3:2,求较大角度数为
.
12.计算:已知∠α=20°20′,则∠α的余角为
.
13.如图,点A在点B的北偏西30°方向,点C在点B的南偏东60°方向.则∠ABC的度数是
.
14.如图,将长方形纸片进行折叠,ED,EF为折痕,A与A'、B与B'、C与C'重合,若∠AED=25°,则∠BEF的度数为
.
15.如图,射线OA的方向是北偏东20度,射线OB的方向是北偏西40度,OD是OB的反向延长线.若OC是∠AOD的平分线,则射线OC的方向是北偏东
度.
三.解答题
16.如图,已知∠ABP与∠CBP互余,∠CBD=32°,BP平分∠ABD.求∠ABP的度数.
17.如图,点O是直线AB上的一点,∠COD是一个直角,OE平分∠BOC.
(1)如图1,当∠AOC=30°,求∠DOE的度数;
(2)如图2,若∠AOC=x°,求∠DOE的度数.(用含有x的代数式表示)
18.如图,已知∠AOC:∠AOB=2:7,OD是∠AOB的平分线,若∠COD=15°,求∠AOC的度数.
19.探究题:如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=100°,将一直角三角形的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?说明理由;
(2)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为
(直接写出结果)
参考答案与试题解析
一.选择题
1.【解答】解:∵10点整,时针指向10,分针指向12,中间相差两大格,
钟表12个数字,每相邻两个数字之间的夹角为30°,
∴10点整分针与时针的夹角是2×30°=60度.
故选:B.
2.【解答】解:①已知∠A=140°,则∠A的补角=40°,原来的说法错误;
②大于直角小于平角的角是钝角,原来的说法错误;
③同角或等角的余角相等是正确的;
④和为180度的两个角互为补角,原来的说法错误.
故其中正确的说法有1个.
故选:D.
3.【解答】解:∠A的补角∠B的度数是:180°﹣115°=65°,
则余角是90°﹣65°=25°.
故选:D.
4.【解答】解:∵∠AOB=∠COD=90°,∠AOD=160°
∴∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣160°=20°.
故选:A.
5.【解答】解:①∵∠AOC=∠BOD=90°,
∴∠AOB+∠BOC=∠BOC+∠COD=90°,
∴∠AOB=∠COD;
②∠AOB+∠COD=90°不一定和是90°;
③若OB平分∠AOC,则∠AOB=∠BOC=45°,
∴∠COD=45°,
∴OC平分∠BOD;
④∵∠AOB=∠COD,
∴∠BOE=∠COE,
∴∠AOE=∠DOE,
∴∠AOD的平分线与∠BOC的平分线是同一条射线.
∴①③④正确,
故选:B.
6.【解答】解:因为一副三角板有30°、45°、60°、90°的角,
又∵45°﹣30°=15°,45°+30°=75°,
45°+60°=105°,45°+90°=135°.
所以用一副三角板可以画出75°、105°、135°等特殊的角.
故选:A.
7.【解答】解:∵方向角是以正北,正南方向为基准,来描述物体所处的方向,
∴射线OP是表示北偏东30°方向可表示为如图.
故选:D.
8.【解答】解:A.如果两个角是同一个角的余角,那么这两个角相等,说法正确;
B.任何有理数都可以用数轴上的点表示,说法正确;
C.绝对值等于它的相反数的数都是负数和0,故原说法错误;
D.若a=b,则,说法正确;
故选:C.
9.【解答】解:如图所示:食指和中指所夹锐角α的度数为:35°.
故选:B.
10.【解答】解:符合题意的示意图为:
.
故选:D.
二.填空题(共5小题)
11.【解答】解:因为两个角的度数之比为3:2,
所以设这两个角的度数分别为(3x)°和(2x)°.
根据题意,列方程,得3x+2x=180,
解这个方程,得x=36,
所以3x=108.
即较大角度数为108°.
故答案为108°.
12.【解答】解:∠α的余角=90°﹣20°20′=69°40′.
故答案为:69°40′.
13.【解答】解:如图:
由题意,得
∠ABD=30°,∠EBC=60°.
∴∠FBC=90°﹣∠EBC=90°﹣60°=30°.
∵∠DBF=90°,
∴∠ABC=∠ABD+∠DBF+∠FBC=30°+90°+30°=150°,
故答案为:150°.
14.【解答】解:根据翻折的性质可知,∠AED=∠A′ED,∠BEF=∠FEB′,
∵∠AED+∠A′ED+∠BEF+∠FEB′=180°,
∴∠AED+∠BEF=90°,
又∵∠AED=25°,
∴∠BEF=65°.
故答案为:65°.
15.【解答】解:∵OB的方向是北偏西40°,OA的方向是北偏东20°,
∴∠AOB=40°+20°=60°,
∴∠AOD=180°﹣60°=120°,
∵OC是∠AOD的平分线,
∴∠AOC=60°,
∵20°+60°=80°,
∴射线OC的方向是北偏东80°;
故答案为:80.
三.解答题(共4小题)
16.【解答】解:∵∠ABP与∠CBP互余,
∴∠ABP+∠CBP90°,
即:∠ABC=90°,
∵∠CBD=32°,
∴∠ABD=90°+32°=122°,
∵BP平分∠ABD.
∴∠ABP=∠DBP=∠ABD=×122°=61°.
17.【解答】解:(1)∵∠AOC=30°,
∴∠BOC=180°﹣∠AOC=150°,
又∵OE平分∠BOC,
∴∠BOE=∠COE=∠BOC=75°,
又∵∠COD=90°,
∴∠DOE=∠COD﹣∠COE=15°;
(2)∵∠AOC=x°,
∴∠BOC=180°﹣∠AOC=(180﹣x)°,
又∵OE平分∠BOC
∴∠BOE=∠COE=∠BOC=(180﹣x)°,
又∵∠COD=90°
∴∠DOE=∠COD﹣∠COE=90°﹣(180﹣x)°=x°
18.【解答】解:∵∠AOC:∠AOB=2:7,
∴设∠AOC=2x°,∠AOB=7x°,
∵OD是∠AOB的平分线,
∴∠AOD=∠AOB=3.5x°,
∵∠DOC=15°,
∴3.5x﹣2x=15,
∴x=10,
即∠AOC=2x°=20°.
19.【解答】解:(1)平分,理由:延长NO,在延长线上取一点D,
∵∠MON=90°∴∠MOD=90°
∴∠MOB+∠NOB=90°,
∠MOC+∠COD=90°,
∵∠MOB=∠MOC,
∴∠NOB=∠COD,
∵∠NOB=∠AOD,
∴∠COD=∠AOD,
∴直线NO平分∠AOC;
(2)分两种情况:
①如图2,∵∠BOC=100°
∴∠AOC=80°,
当直线ON恰好平分锐角∠AOC时,∠AOD=∠COD=40°,
∴∠BON=40°,∠BOM=50°,
即逆时针旋转的角度为50°,
由题意得,5°t=50°
解得t=10(s);
②如图3,当NO平分∠AOC时,∠NOA=40°,
∴∠AOM=50°,
即逆时针旋转的角度为:180°+50°=230°
4.4 课题学习 设计制作长方体形状的包装纸盒
一、选择题
1.下列四个平面图形中,不能折叠成无盖的长方体盒子的是
( )
2.图是正方体的一种展开图,如果将其折叠成原来的正方体,那么与边a重合的边是
( )
A.d B.e
C.f D.i
二、非选择题
3.图是某些几何体的展开图,请填出这些几何体的名称.
4.图是一个无盖的长方体纸盒展开图,纸盒的底面积为600
cm2.
求:(1)纸盒的高为多少厘米;
(2)展开图的周长为多少厘米.
图
5.图是一个食品包装盒的展开图.请根据图中所标的尺寸,计算这个食品包装盒的表面积和体积.
6.图是一个食品包装盒的展开图(其中的六边形的六条边相等).
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积.
7.一个正方体的展开图已有一部分(如图),还有一个正方形未画出,现有10个位置可供选择,则放在哪些位置能围成正方体,放在哪些位置不能围成正方体?仔细观察图4-4-7,或许你还要动手做做呢!
放在 可围成正方体,放在 不可以围成正方体(填序号).?
参考答案
一、选择题
1.A
2.A
二、非选择题
3.圆锥 三棱柱 长方体
4.解:(1)设底面长为3x
cm,宽为2x
cm.
根据题意,得2x·3x=600,即x2=100,
解得x=10(负值已舍去).
故纸盒的高为10
cm.
(2)展开图的周长为2×(5×10+4×10)=180(cm).
5.解:这个食品包装盒的表面积为2×b2+4×ab=2b2+4ab.体积为b2×a=ab2.
6.解:(1)这个多面体是六棱柱.
(2)这个多面体的侧面积为6ab.
7.①⑦⑧⑨ ②③④⑤⑥⑩
