苏科版数学八年级上册 5.2 平面直角坐标系 教案
文档属性
| 名称 | 苏科版数学八年级上册 5.2 平面直角坐标系 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 705.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览


文档简介
凤凰初中数学配套教学软件_教学设计
数学教学设计
5.2 平面直角坐标系(1)
教学目标 1.认识并能画出平面直角坐标系,知道点的坐标及象限的含义;2.能在给定的直角坐标系中,由点的位置写出它的坐标和由点的坐标指出它的位置;3.经历画坐标系,由点找坐标等过程,发展数形结合意识.
教学重点 认识并能画出平面直角坐标系,根据所给的直角坐标系中给出的点的位置写出点的坐标.
教学难点 横(或纵)坐标相同的点的连线与坐标轴的关系的探究,以及坐标轴上点的坐标有什么特点的总结.
教学过程(教师) 学生活动 设计思路
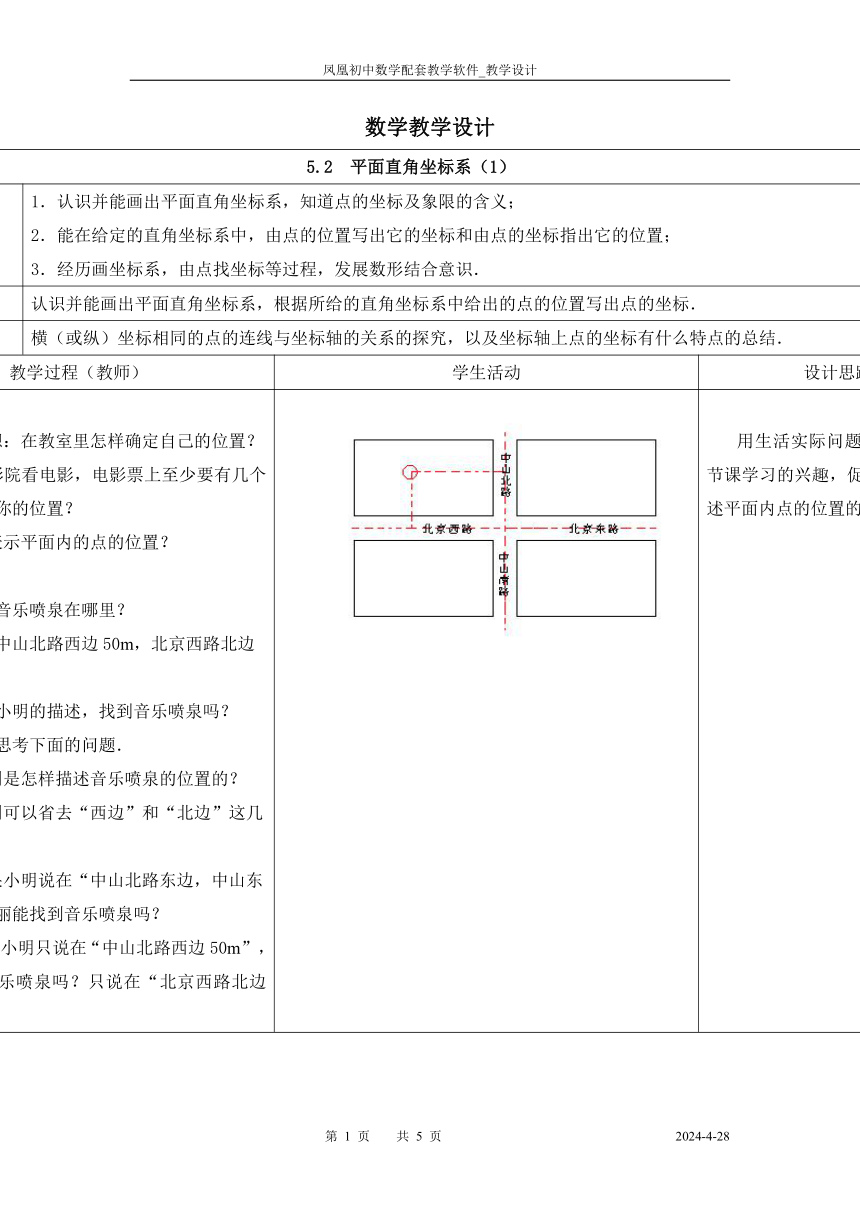
问题的引入1.想一想:在教室里怎样确定自己的位置?2.上电影院看电影,电影票上至少要有几个数字才能确定你的位置?3.怎样表示平面内的点的位置?小丽问:音乐喷泉在哪里?小明说:中山北路西边50m,北京西路北边30m.小丽能按小明的描述,找到音乐喷泉吗?请同学们思考下面的问题.(1)小明是怎样描述音乐喷泉的位置的?(2)小明可以省去“西边”和“北边”这几个字吗?(3)如果小明说在“中山北路东边,中山东路北边”,小丽能找到音乐喷泉吗?(4)如果小明只说在“中山北路西边50m”, 小丽能找到音乐喷泉吗?只说在“北京西路北边30m”呢? 用生活实际问题激发学生对本节课学习的兴趣,促进其对如何描述平面内点的位置的问题的思考.
探索规律,揭示新知生活中,我们常要描述各种目标的位置.如果将东西向的北京路和南北向的中山路看成两条互相垂直的数轴,十字路口为它们的公共原点,那么中山北路西边50m可记为-50,北京西路北边30m可记为+30,音乐喷泉的位置就可以用一对实数(-50,30)来描述. 平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系.水平方向的数轴称为x轴或横轴,竖直方向的数轴称为y轴或纵轴,它们统称为坐标轴.两条坐标轴的公共原点称为坐标原点,通常记为O.x轴和y轴将平面分成的4个区域称为象限,按逆时针顺序分别记为第一象限、第二象限、第三象限、第四象限.但必须注意,坐标轴上的点不属于任何象限. 从学生的生活实践经验,找出音乐喷泉的位置.就在这个图的基础上去掉单位,再加上两条数轴,学生就很容易理解确定音乐喷泉的位置要用两个数来表示,引出直角坐标系的雏形,再把这个实际问题迁移到数学上来,建立直角坐标系也就迎刃而解了,同时也就解决了为什么平面上点的位置必须用一对有序实数对表示这一难点.这样学生思路清楚,理解起来很方便.整节课都是在教师指导下学生自己完成的.这部分内容以老师讲授为主,使学生了解有关概念.
在直角坐标系中,由一对有序实数(a,b),可以确定一个点P的位置:过x轴上表示实数的点画x轴的垂线,过y轴上表示实数的点画y轴的垂线,这两条垂线的交点,即为点P.反过来,如果点Q是直角坐标系中一点,你能找到一对相应的有序实数(m,n)吗?在直角坐标系中,一对有序实数可以确定一个点的位置;反之,任意一点的位置都可以用一对有序实数表示.这样的有序实数对叫做点的坐标.右图中点P的坐标为(a,b),其中a称为点P的横坐标,b称为点P的纵坐标,横坐标应写在纵坐标的前面.由点Q的位置可以知道它的坐标为(m,n).点的坐标通常与表示该点的大写字母写在一起,如P(a,b),Q(m,n). 让学生自学后分小组进行讨论、交流,培养学生的自学能力,发现新问题的意识.
尝试反馈,领悟新知例 1 在直角坐标系中,描出下列各点的位置:A (4,1),B(-1,4),C(-4,-2),D(3,-2),E( 0, 1 ),F( -4, 0 ) .例2 写出右图中A、B、C 各点的坐标.注意:1.开始要遵照前面点的坐标的概念,从图上的点分别向两轴作垂线,得出坐标.探究、讨论:第一象限的点的坐标有什么特点?其他象限的点呢?2.坐标轴上的点有什么特点?在x轴上的点,纵坐标等于0;在y轴上的点,横坐标等于0.探索:点的坐标的几何意义.已知点A(a,b),过点A作x轴的垂线,垂足为B,过点A作y轴的垂线,垂足为C.(1)四边形OBAC是矩形吗?(2)线段OC的长度与点A的坐标有什么数量关系?(3)线段OB的长度与点A的坐标有什么数量关系? 例题可由学生自己来完成,同学们互相改正错误.学生尝试把点的坐标具体化,并画图,分组讨论点A分别在第一、二、三、四象限时,线段OB、OC的长度与点A的坐标的关系.再由学生总结:线段OB的长度就是|a|,线段OC的长度就是|b|. 问题的解决,让学生尝试解决更复杂更难的问题,进一步激发其探求的欲望,培养学生良好的学习品德.学生应用从研究简单问题获得的经验解决较为复杂的问题,学习处理复杂问题的研究方法和手段.
课堂练习一、课本P122练习1、2.二、判断.1.对于坐标平面内的任一点,都有唯一的一对有序实数与它对应.( )2.在直角坐标系内,原点的坐标是0.( ) 3.点 A(a ,-b )在第二象限,则点B(-a , b )在第四象限. ( )4.若点 P 的坐标为(a,b),且a·b=0,则点P 一定在坐标原点. ( )三、已知 P 点坐标为(2 a+1,a-3),( 1 ) 点 P 在 x 轴上,则a= ; ( 2 ) 点 P 在 y 轴上,则a= . 四、若点 P(x,y)在第四象限,| x |=5,| y |=4,则 P 点的坐标为 . 学生独立完成.
归纳小结,巩固提高1.什么是平面直角坐标系?2.平面内点的坐标的意义,你理解了吗?3.在学习过程中你还存在哪些问题? 尝试对知识方法进行归纳、提炼、总结,形成理性的认识, 内化数学的方法和经验. 试对所学知识进行反思、归纳和总结.会对知识进行提炼,体会数学的思想和应用,将感性的认识升华为理性的认识.
布置作业,巩固新知1.课本129页1、2.2.补充习题.
第 1 页 共 5 页 2024-1-13
数学教学设计
5.2 平面直角坐标系(1)
教学目标 1.认识并能画出平面直角坐标系,知道点的坐标及象限的含义;2.能在给定的直角坐标系中,由点的位置写出它的坐标和由点的坐标指出它的位置;3.经历画坐标系,由点找坐标等过程,发展数形结合意识.
教学重点 认识并能画出平面直角坐标系,根据所给的直角坐标系中给出的点的位置写出点的坐标.
教学难点 横(或纵)坐标相同的点的连线与坐标轴的关系的探究,以及坐标轴上点的坐标有什么特点的总结.
教学过程(教师) 学生活动 设计思路
问题的引入1.想一想:在教室里怎样确定自己的位置?2.上电影院看电影,电影票上至少要有几个数字才能确定你的位置?3.怎样表示平面内的点的位置?小丽问:音乐喷泉在哪里?小明说:中山北路西边50m,北京西路北边30m.小丽能按小明的描述,找到音乐喷泉吗?请同学们思考下面的问题.(1)小明是怎样描述音乐喷泉的位置的?(2)小明可以省去“西边”和“北边”这几个字吗?(3)如果小明说在“中山北路东边,中山东路北边”,小丽能找到音乐喷泉吗?(4)如果小明只说在“中山北路西边50m”, 小丽能找到音乐喷泉吗?只说在“北京西路北边30m”呢? 用生活实际问题激发学生对本节课学习的兴趣,促进其对如何描述平面内点的位置的问题的思考.
探索规律,揭示新知生活中,我们常要描述各种目标的位置.如果将东西向的北京路和南北向的中山路看成两条互相垂直的数轴,十字路口为它们的公共原点,那么中山北路西边50m可记为-50,北京西路北边30m可记为+30,音乐喷泉的位置就可以用一对实数(-50,30)来描述. 平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系.水平方向的数轴称为x轴或横轴,竖直方向的数轴称为y轴或纵轴,它们统称为坐标轴.两条坐标轴的公共原点称为坐标原点,通常记为O.x轴和y轴将平面分成的4个区域称为象限,按逆时针顺序分别记为第一象限、第二象限、第三象限、第四象限.但必须注意,坐标轴上的点不属于任何象限. 从学生的生活实践经验,找出音乐喷泉的位置.就在这个图的基础上去掉单位,再加上两条数轴,学生就很容易理解确定音乐喷泉的位置要用两个数来表示,引出直角坐标系的雏形,再把这个实际问题迁移到数学上来,建立直角坐标系也就迎刃而解了,同时也就解决了为什么平面上点的位置必须用一对有序实数对表示这一难点.这样学生思路清楚,理解起来很方便.整节课都是在教师指导下学生自己完成的.这部分内容以老师讲授为主,使学生了解有关概念.
在直角坐标系中,由一对有序实数(a,b),可以确定一个点P的位置:过x轴上表示实数的点画x轴的垂线,过y轴上表示实数的点画y轴的垂线,这两条垂线的交点,即为点P.反过来,如果点Q是直角坐标系中一点,你能找到一对相应的有序实数(m,n)吗?在直角坐标系中,一对有序实数可以确定一个点的位置;反之,任意一点的位置都可以用一对有序实数表示.这样的有序实数对叫做点的坐标.右图中点P的坐标为(a,b),其中a称为点P的横坐标,b称为点P的纵坐标,横坐标应写在纵坐标的前面.由点Q的位置可以知道它的坐标为(m,n).点的坐标通常与表示该点的大写字母写在一起,如P(a,b),Q(m,n). 让学生自学后分小组进行讨论、交流,培养学生的自学能力,发现新问题的意识.
尝试反馈,领悟新知例 1 在直角坐标系中,描出下列各点的位置:A (4,1),B(-1,4),C(-4,-2),D(3,-2),E( 0, 1 ),F( -4, 0 ) .例2 写出右图中A、B、C 各点的坐标.注意:1.开始要遵照前面点的坐标的概念,从图上的点分别向两轴作垂线,得出坐标.探究、讨论:第一象限的点的坐标有什么特点?其他象限的点呢?2.坐标轴上的点有什么特点?在x轴上的点,纵坐标等于0;在y轴上的点,横坐标等于0.探索:点的坐标的几何意义.已知点A(a,b),过点A作x轴的垂线,垂足为B,过点A作y轴的垂线,垂足为C.(1)四边形OBAC是矩形吗?(2)线段OC的长度与点A的坐标有什么数量关系?(3)线段OB的长度与点A的坐标有什么数量关系? 例题可由学生自己来完成,同学们互相改正错误.学生尝试把点的坐标具体化,并画图,分组讨论点A分别在第一、二、三、四象限时,线段OB、OC的长度与点A的坐标的关系.再由学生总结:线段OB的长度就是|a|,线段OC的长度就是|b|. 问题的解决,让学生尝试解决更复杂更难的问题,进一步激发其探求的欲望,培养学生良好的学习品德.学生应用从研究简单问题获得的经验解决较为复杂的问题,学习处理复杂问题的研究方法和手段.
课堂练习一、课本P122练习1、2.二、判断.1.对于坐标平面内的任一点,都有唯一的一对有序实数与它对应.( )2.在直角坐标系内,原点的坐标是0.( ) 3.点 A(a ,-b )在第二象限,则点B(-a , b )在第四象限. ( )4.若点 P 的坐标为(a,b),且a·b=0,则点P 一定在坐标原点. ( )三、已知 P 点坐标为(2 a+1,a-3),( 1 ) 点 P 在 x 轴上,则a= ; ( 2 ) 点 P 在 y 轴上,则a= . 四、若点 P(x,y)在第四象限,| x |=5,| y |=4,则 P 点的坐标为 . 学生独立完成.
归纳小结,巩固提高1.什么是平面直角坐标系?2.平面内点的坐标的意义,你理解了吗?3.在学习过程中你还存在哪些问题? 尝试对知识方法进行归纳、提炼、总结,形成理性的认识, 内化数学的方法和经验. 试对所学知识进行反思、归纳和总结.会对知识进行提炼,体会数学的思想和应用,将感性的认识升华为理性的认识.
布置作业,巩固新知1.课本129页1、2.2.补充习题.
第 1 页 共 5 页 2024-1-13
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
