人教版九年级上册数学学案:24.3正多边形和圆
文档属性
| 名称 | 人教版九年级上册数学学案:24.3正多边形和圆 | 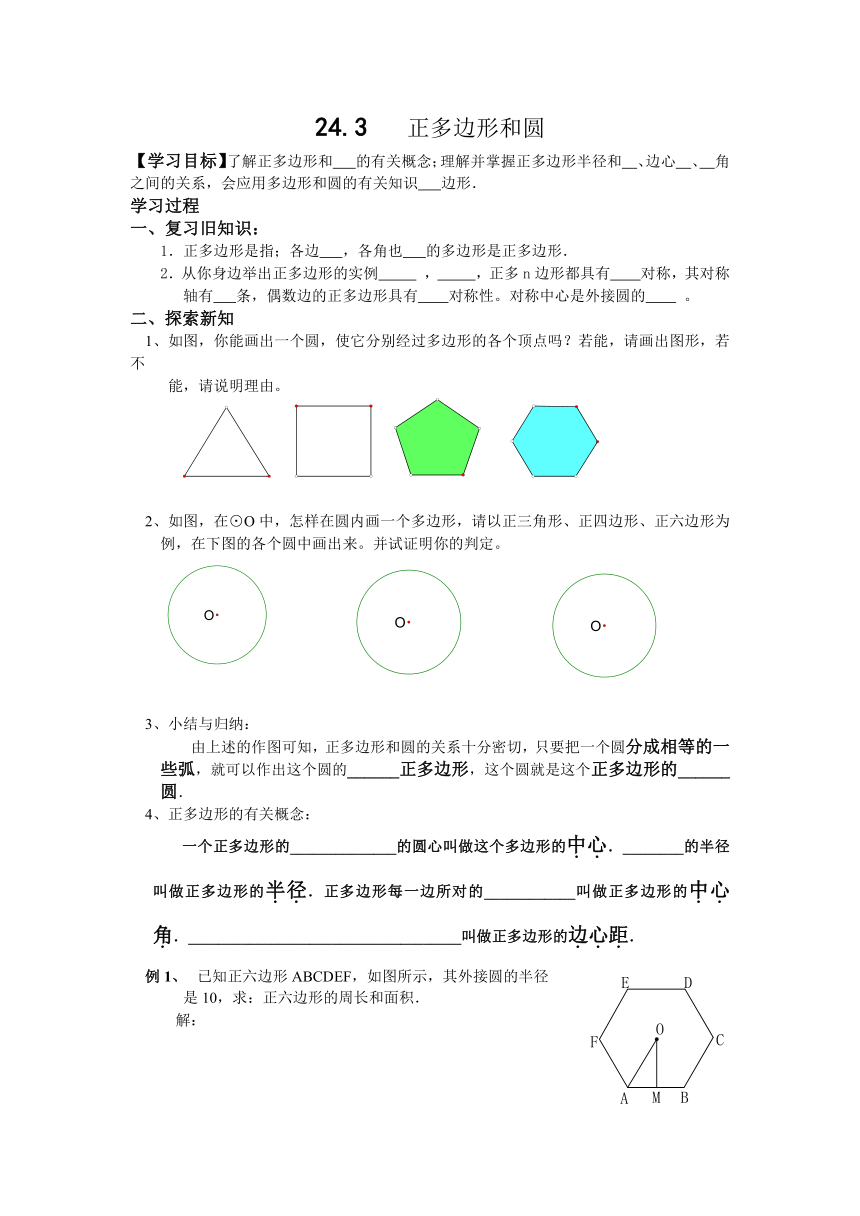 | |
| 格式 | zip | ||
| 文件大小 | 31.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 08:38:15 | ||
图片预览

文档简介
24.3
正多边形和圆
【学习目标】了解正多边形和
的有关概念;理解并掌握正多边形半径和
、边心
、
角之间的关系,会应用多边形和圆的有关知识
边形.
学习过程
一、复习旧知识:
1.正多边形是指;各边
,各角也
的多边形是正多边形.
2.从你身边举出正多边形的实例
,
,正多n边形都具有
对称,其对称轴有
条,偶数边的正多边形具有
对称性。对称中心是外接圆的
。
二、探索新知
1、如图,你能画出一个圆,使它分别经过多边形的各个顶点吗?若能,请画出图形,若不
能,请说明理由。
2、如图,在⊙O中,怎样在圆内画一个多边形,请以正三角形、正四边形、正六边形为例,在下图的各个圆中画出来。并试证明你的判定。
3、小结与归纳:
由上述的作图可知,正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的______正多边形,这个圆就是这个正多边形的______圆.
4、正多边形的有关概念:
一个正多边形的______________的圆心叫做这个多边形的中心.________的半径叫做正多边形的半径.正多边形每一边所对的____________叫做正多边形的中心角.____________________________________叫做正多边形的边心距.
已知正六边形ABCDEF,如图所示,其外接圆的半径
是10,求:正六边形的周长和面积.
解:
三、练习巩固
1.如图1所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是(
).
A.60°
B.45°
C.30°
D.22.5°
(1)
(2)
(3)
2.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是(
).
A.36°
B.60°
C.72°
D.108°
3.若半径为5cm的一段弧长等于半径为2cm的圆的周长,则这段弧所对的圆心角为(
)
A.18°
B.36°
C.72°
D.144°
4.已知正六边形边长为2,则它的内切圆面积为_______.
5.在△ABC中,∠ACB=90°,∠B=30°,以C为圆心,CA长为半径的圆交AB于D,
如图2所示,若AC=6,则AD的长为________.
6.四边形ABCD为⊙O的内接梯形,如图3所示,AB∥CD,且CD为直径,如果⊙O的半径等于r,∠C=60°,那图中△OAB的边长AB是______;△ODA的周长是_______;∠BOC的度数是________.
四、综合提高题
1.等边△ABC的边长为4,求其内切圆的内接正方形DEFG的面积.
2.如图所示,已知⊙O的周长等于6cm,求以它的半径为边长的正六边形ABCDEF的面积.
五、课后作业
1.如图所示,已知⊙O的周长等于6cm,求以它的半径为边长的正六边形ABCDEF的面积.
2.(完成下面的表格有关正多边形的计算)
多边形的边数
内角
中心角
半径
边长
边心距
周长
面积
3
6
4
6
6
6
六、教学反思:
正多边形和圆
【学习目标】了解正多边形和
的有关概念;理解并掌握正多边形半径和
、边心
、
角之间的关系,会应用多边形和圆的有关知识
边形.
学习过程
一、复习旧知识:
1.正多边形是指;各边
,各角也
的多边形是正多边形.
2.从你身边举出正多边形的实例
,
,正多n边形都具有
对称,其对称轴有
条,偶数边的正多边形具有
对称性。对称中心是外接圆的
。
二、探索新知
1、如图,你能画出一个圆,使它分别经过多边形的各个顶点吗?若能,请画出图形,若不
能,请说明理由。
2、如图,在⊙O中,怎样在圆内画一个多边形,请以正三角形、正四边形、正六边形为例,在下图的各个圆中画出来。并试证明你的判定。
3、小结与归纳:
由上述的作图可知,正多边形和圆的关系十分密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的______正多边形,这个圆就是这个正多边形的______圆.
4、正多边形的有关概念:
一个正多边形的______________的圆心叫做这个多边形的中心.________的半径叫做正多边形的半径.正多边形每一边所对的____________叫做正多边形的中心角.____________________________________叫做正多边形的边心距.
已知正六边形ABCDEF,如图所示,其外接圆的半径
是10,求:正六边形的周长和面积.
解:
三、练习巩固
1.如图1所示,正六边形ABCDEF内接于⊙O,则∠ADB的度数是(
).
A.60°
B.45°
C.30°
D.22.5°
(1)
(2)
(3)
2.圆内接正五边形ABCDE中,对角线AC和BD相交于点P,则∠APB的度数是(
).
A.36°
B.60°
C.72°
D.108°
3.若半径为5cm的一段弧长等于半径为2cm的圆的周长,则这段弧所对的圆心角为(
)
A.18°
B.36°
C.72°
D.144°
4.已知正六边形边长为2,则它的内切圆面积为_______.
5.在△ABC中,∠ACB=90°,∠B=30°,以C为圆心,CA长为半径的圆交AB于D,
如图2所示,若AC=6,则AD的长为________.
6.四边形ABCD为⊙O的内接梯形,如图3所示,AB∥CD,且CD为直径,如果⊙O的半径等于r,∠C=60°,那图中△OAB的边长AB是______;△ODA的周长是_______;∠BOC的度数是________.
四、综合提高题
1.等边△ABC的边长为4,求其内切圆的内接正方形DEFG的面积.
2.如图所示,已知⊙O的周长等于6cm,求以它的半径为边长的正六边形ABCDEF的面积.
五、课后作业
1.如图所示,已知⊙O的周长等于6cm,求以它的半径为边长的正六边形ABCDEF的面积.
2.(完成下面的表格有关正多边形的计算)
多边形的边数
内角
中心角
半径
边长
边心距
周长
面积
3
6
4
6
6
6
六、教学反思:
同课章节目录
