3.2 圆的对称性 课件(共32张PPT)
文档属性
| 名称 | 3.2 圆的对称性 课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 21:32:16 | ||
图片预览


文档简介
(共32张PPT)
第三章
圆
3.2
圆的对称性
北师大版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
【知识与技能】
理解圆的旋转不变性,掌握圆心角、弧、弦之间的关系定理及其推论,会用这三者之间的关系进行简单的证明.
【过程与方法】
通过本节课的学习培养学生观察、实验、探究、归纳和概括能力.
【情感态度】
结合本课教学内容向学生渗透事物之间可相互转化的辩证唯物主义教育;渗透圆的内在美.
【教学重点】
圆心角、弧、弦之间的关系定理及其推论.
【教学难点】
对定理中“在同圆或等圆中”前提条件的理解,以及从感性到理性的认识,发现归纳能力的培养.
情景导学
2
情景导学
熊宝宝要过生日了!要把蛋糕平均分成四块,你会分吗?
新课进行时
3
新课进行时
核心知识点一
圆的对称性
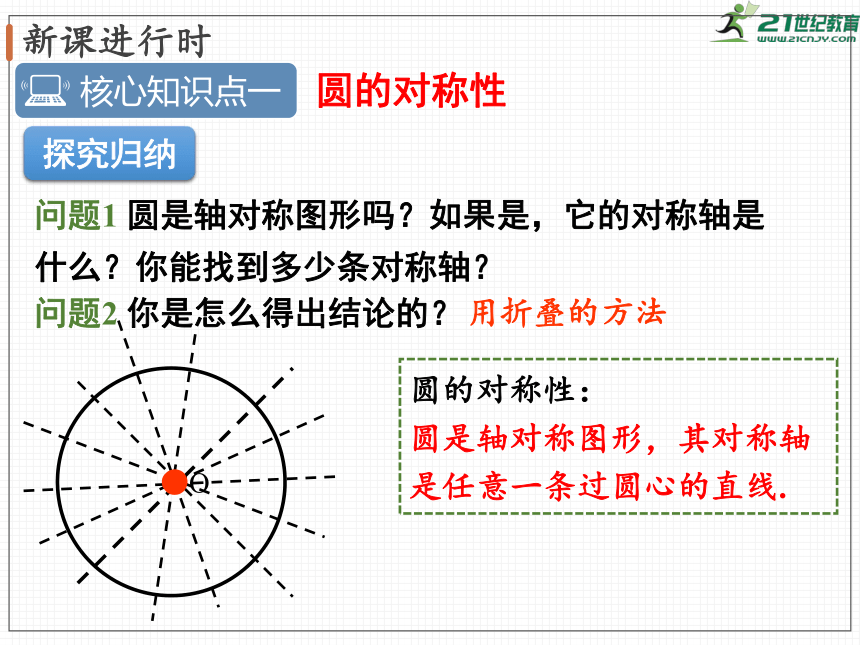
问题1
圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
问题2
你是怎么得出结论的?
圆的对称性:
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
用折叠的方法
●O
探究归纳
新课进行时
.
O
A
B
180°
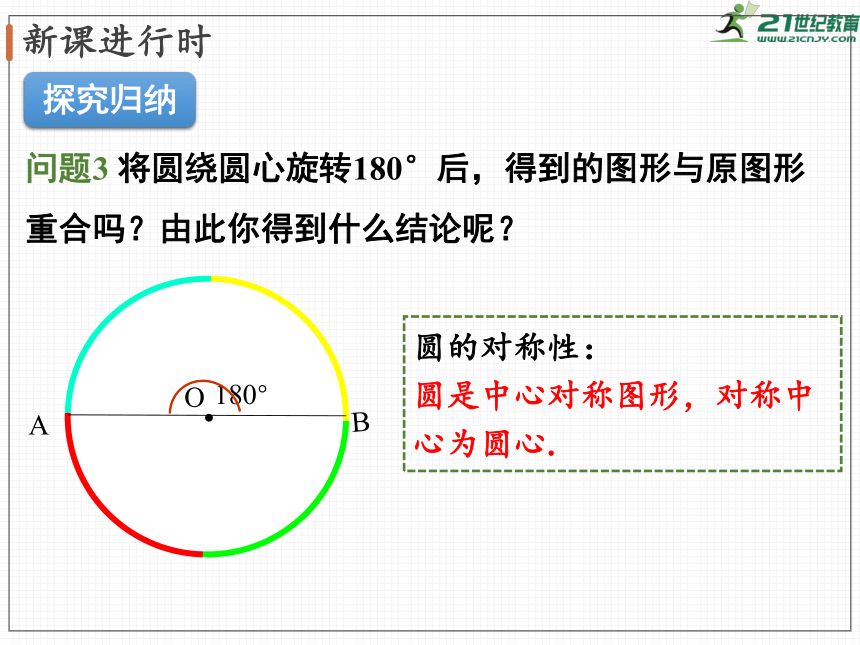
问题3
将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
探究归纳
圆的对称性:
圆是中心对称图形,对称中心为圆心.
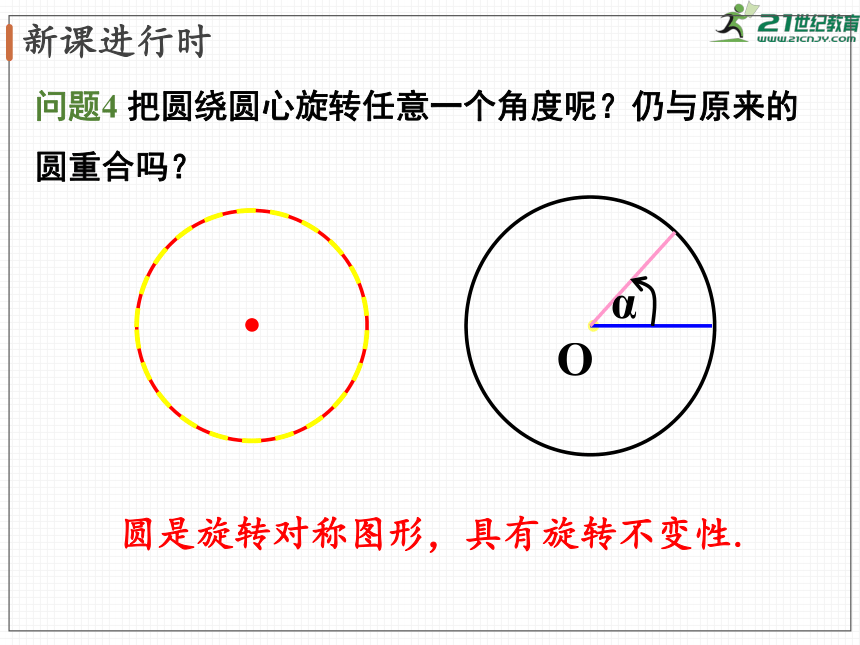
问题4
把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
圆是旋转对称图形,具有旋转不变性.
·
新课进行时
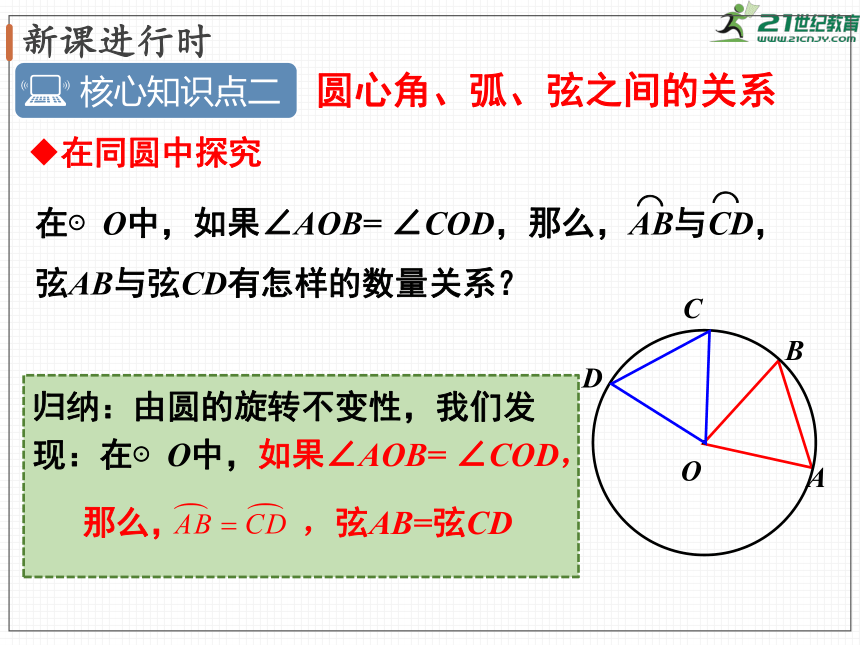
在同圆中探究
在⊙O中,如果∠AOB=
∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
C
·
O
A
B
D
归纳:由圆的旋转不变性,我们发现:在⊙O中,如果∠AOB=
∠COD,
那么,
,弦AB=弦CD
新课进行时
核心知识点二
圆心角、弧、弦之间的关系
O
′
·
O
A
B
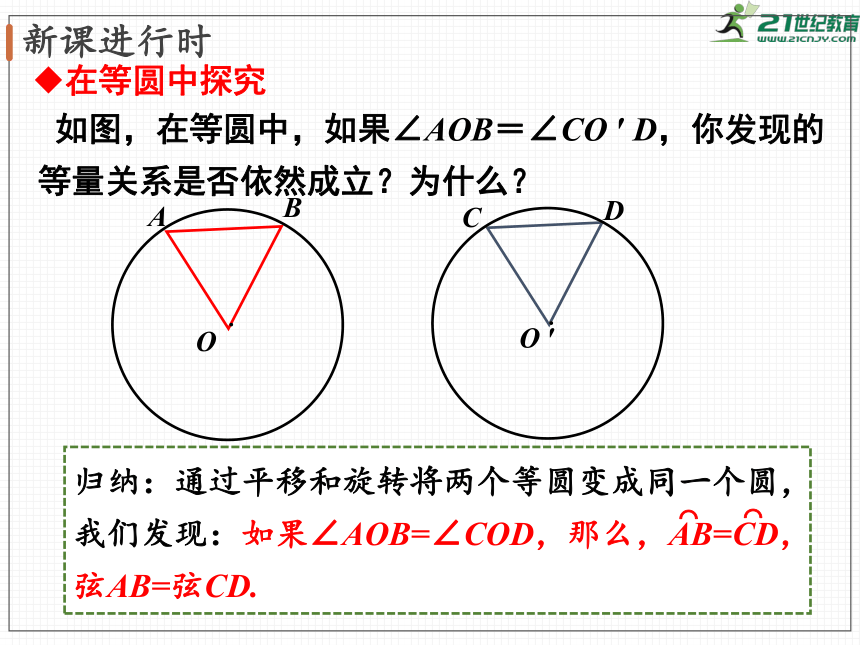
如图,在等圆中,如果∠AOB=∠CO
′
D,你发现的等量关系是否依然成立?为什么?
·
C
D
在等圆中探究
归纳:通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠COD,那么,AB=CD,弦AB=弦CD.
⌒
⌒
新课进行时
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
①∠AOB=∠COD
②AB=CD
⌒
⌒
③AB=CD
A
B
O
D
C
要点归纳
弧、弦与圆心角的关系定理
新课进行时
想一想:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
新课进行时
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
在同圆或等圆中
题设
结论
新课进行时
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧、弦与圆心角关系定理的推论
要点归纳
新课进行时
×
×
√
抢答题
1.等弦所对的弧相等.
(
)
2.等弧所对的弦相等.
(
)
3.圆心角相等,所对的弦相等.
(
)
新课进行时
典例精析
例1
如图,AB,DE是⊙O
的直径,C是⊙O
上的一点,
且AD=CE.BE和CE的大小有什么关系?为什么?
·
E
B
C
O
A
D
解:BE=CE.理由是:
∵∠AOD=∠BOE,
∴AD=BE.
又∵AD=CE,
∴BE=CE.
∴BE=CE.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
新课进行时
核心知识点三
关系定理及推论的运用
解:
∵
例2
如图,AB是⊙O
的直径,
∠COD=35°,求∠AOE
的度数.
·
A
O
B
C
D
E
新课进行时
证明:
∴
AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴
△ABC是等边三角形
,
AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
例3
如图,在⊙O中,
AB=AC
,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
·
A
B
C
O
⌒
⌒
温馨提示:本题告诉我们,弧、圆心角、弦灵活转化是解题的关键.
∵AB=CD,
⌒
⌒
新课进行时
填一填:
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么_________,____________.
(2)如果
,那么_________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
·
C
A
B
D
E
F
O
AB=CD
AB=CD
AB=CD
(
(
∠AOB=
∠COD
∠AOB=
∠COD
AB=CD
(
(
AB=CD
(
(
针对训练
新课进行时
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
解:OE=OF.
理由如下:
·
C
A
B
D
E
F
O
新课进行时
知识小结
4
知识小结
圆心角
相等
弧
相等
弦
相等
弦、弧、圆心角的关系定理
在同圆或等圆中
应用提醒
①要注意前提条件;
②要灵活转化.
圆
圆是轴对称图形,其对称轴是任意一条过圆心的直线;
圆是中心对称图形,对称中心为圆心.
随堂演练
5
随堂演练
1.如果两个圆心角相等,那么
(
)
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
2.弦长等于半径的弦所对的圆心角等于
.
D
60
°
3.在同圆中,圆心角∠AOB=2∠COD,则AB与CD的关系是(
)
⌒
⌒
A
A.
AB=2CD
⌒
⌒
B.
AB>CD
⌒
⌒
C.
AB⌒
⌒
D.
不能确定
4.如图,已知AB、CD为⊙O的两条弦,
求证:AB=CD.
.
C
A
B
D
O
随堂演练
能力提升:
我们已经知道在⊙O中,如果2∠AOB=∠COD,则CD=2AB,那么CD=2AB也成立吗?若成立,请说明理由;若不成立,那它们之间的关系又是什么?
⌒
⌒
解:CD=2AB不成立.理由如下:
取
的中点E,连接OE,CE,DE.
那么∠AOB=∠COE=∠DOE,
所以弦AB=CE=DE,
在△CDE中,CE+DE>CD,即CD<2AB.
A
B
C
D
E
O
随堂演练
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第三章
圆
3.2
圆的对称性
北师大版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
【知识与技能】
理解圆的旋转不变性,掌握圆心角、弧、弦之间的关系定理及其推论,会用这三者之间的关系进行简单的证明.
【过程与方法】
通过本节课的学习培养学生观察、实验、探究、归纳和概括能力.
【情感态度】
结合本课教学内容向学生渗透事物之间可相互转化的辩证唯物主义教育;渗透圆的内在美.
【教学重点】
圆心角、弧、弦之间的关系定理及其推论.
【教学难点】
对定理中“在同圆或等圆中”前提条件的理解,以及从感性到理性的认识,发现归纳能力的培养.
情景导学
2
情景导学
熊宝宝要过生日了!要把蛋糕平均分成四块,你会分吗?
新课进行时
3
新课进行时
核心知识点一
圆的对称性
问题1
圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
问题2
你是怎么得出结论的?
圆的对称性:
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
用折叠的方法
●O
探究归纳
新课进行时
.
O
A
B
180°
问题3
将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
探究归纳
圆的对称性:
圆是中心对称图形,对称中心为圆心.
问题4
把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
圆是旋转对称图形,具有旋转不变性.
·
新课进行时
在同圆中探究
在⊙O中,如果∠AOB=
∠COD,那么,AB与CD,弦AB与弦CD有怎样的数量关系?
⌒
⌒
C
·
O
A
B
D
归纳:由圆的旋转不变性,我们发现:在⊙O中,如果∠AOB=
∠COD,
那么,
,弦AB=弦CD
新课进行时
核心知识点二
圆心角、弧、弦之间的关系
O
′
·
O
A
B
如图,在等圆中,如果∠AOB=∠CO
′
D,你发现的等量关系是否依然成立?为什么?
·
C
D
在等圆中探究
归纳:通过平移和旋转将两个等圆变成同一个圆,我们发现:如果∠AOB=∠COD,那么,AB=CD,弦AB=弦CD.
⌒
⌒
新课进行时
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
①∠AOB=∠COD
②AB=CD
⌒
⌒
③AB=CD
A
B
O
D
C
要点归纳
弧、弦与圆心角的关系定理
新课进行时
想一想:定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图.
A
B
O
D
C
新课进行时
如果弧相等
那么
弧所对的圆心角相等
弧所对的弦相等
如果弦相等
那么
弦所对应的圆心角相等
弦所对应的优弧相等
弦所对应的劣弧相等
如果圆心角相等
那么
圆心角所对的弧相等
圆心角所对的弦相等
在同圆或等圆中
题设
结论
新课进行时
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
弧、弦与圆心角关系定理的推论
要点归纳
新课进行时
×
×
√
抢答题
1.等弦所对的弧相等.
(
)
2.等弧所对的弦相等.
(
)
3.圆心角相等,所对的弦相等.
(
)
新课进行时
典例精析
例1
如图,AB,DE是⊙O
的直径,C是⊙O
上的一点,
且AD=CE.BE和CE的大小有什么关系?为什么?
·
E
B
C
O
A
D
解:BE=CE.理由是:
∵∠AOD=∠BOE,
∴AD=BE.
又∵AD=CE,
∴BE=CE.
∴BE=CE.
⌒
⌒
⌒
⌒
⌒
⌒
⌒
⌒
新课进行时
核心知识点三
关系定理及推论的运用
解:
∵
例2
如图,AB是⊙O
的直径,
∠COD=35°,求∠AOE
的度数.
·
A
O
B
C
D
E
新课进行时
证明:
∴
AB=AC.△ABC是等腰三角形.
又∠ACB=60°,
∴
△ABC是等边三角形
,
AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
例3
如图,在⊙O中,
AB=AC
,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC.
·
A
B
C
O
⌒
⌒
温馨提示:本题告诉我们,弧、圆心角、弦灵活转化是解题的关键.
∵AB=CD,
⌒
⌒
新课进行时
填一填:
如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么_________,____________.
(2)如果
,那么_________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
·
C
A
B
D
E
F
O
AB=CD
AB=CD
AB=CD
(
(
∠AOB=
∠COD
∠AOB=
∠COD
AB=CD
(
(
AB=CD
(
(
针对训练
新课进行时
(4)如果AB=CD,OE⊥AB于E,OF⊥CD于F,OE与OF相等吗?为什么?
解:OE=OF.
理由如下:
·
C
A
B
D
E
F
O
新课进行时
知识小结
4
知识小结
圆心角
相等
弧
相等
弦
相等
弦、弧、圆心角的关系定理
在同圆或等圆中
应用提醒
①要注意前提条件;
②要灵活转化.
圆
圆是轴对称图形,其对称轴是任意一条过圆心的直线;
圆是中心对称图形,对称中心为圆心.
随堂演练
5
随堂演练
1.如果两个圆心角相等,那么
(
)
A.这两个圆心角所对的弦相等
B.这两个圆心角所对的弧相等
C.这两个圆心角所对的弦的弦心距相等
D.以上说法都不对
2.弦长等于半径的弦所对的圆心角等于
.
D
60
°
3.在同圆中,圆心角∠AOB=2∠COD,则AB与CD的关系是(
)
⌒
⌒
A
A.
AB=2CD
⌒
⌒
B.
AB>CD
⌒
⌒
C.
AB
⌒
D.
不能确定
4.如图,已知AB、CD为⊙O的两条弦,
求证:AB=CD.
.
C
A
B
D
O
随堂演练
能力提升:
我们已经知道在⊙O中,如果2∠AOB=∠COD,则CD=2AB,那么CD=2AB也成立吗?若成立,请说明理由;若不成立,那它们之间的关系又是什么?
⌒
⌒
解:CD=2AB不成立.理由如下:
取
的中点E,连接OE,CE,DE.
那么∠AOB=∠COE=∠DOE,
所以弦AB=CE=DE,
在△CDE中,CE+DE>CD,即CD<2AB.
A
B
C
D
E
O
随堂演练
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
