3.8 圆内接正多边形 课件(共32张PPT)
文档属性
| 名称 | 3.8 圆内接正多边形 课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
第三章
圆
3.8
圆内接正多边形
北师大版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
【知识与技能】
1.掌握圆内接正多边形、外接圆、边心距、中心角的概念.
2.正多边形的画法.
【过程与方法】
通过作图的过程,提高学生的几何语言表达能力和合情推理能力.
【情感态度】
在学生动手操作的过程中,增强学生的数学应用意识,提高学生学习数学的兴趣和积极性,培养学生主动探索的精神,培养学生合作交流和创新意识.
【教学重点】
圆内接正多边形、外接圆、边心距、中心角的概念.
【教学难点】
圆内接正多边形、外接圆、边心距、中心角的概念.
情景导学
2
情景导学
问题:观看大屏幕上这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗?
观察与思考
新课进行时
3
新课进行时
核心知识点一
正多边形的回顾
问题1
什么叫做正多边形?
各边相等,各角也相等的多边形叫做正多边形.
问题2
矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
注意
正多边形
各边相等
各角相等
缺一不可
新课进行时
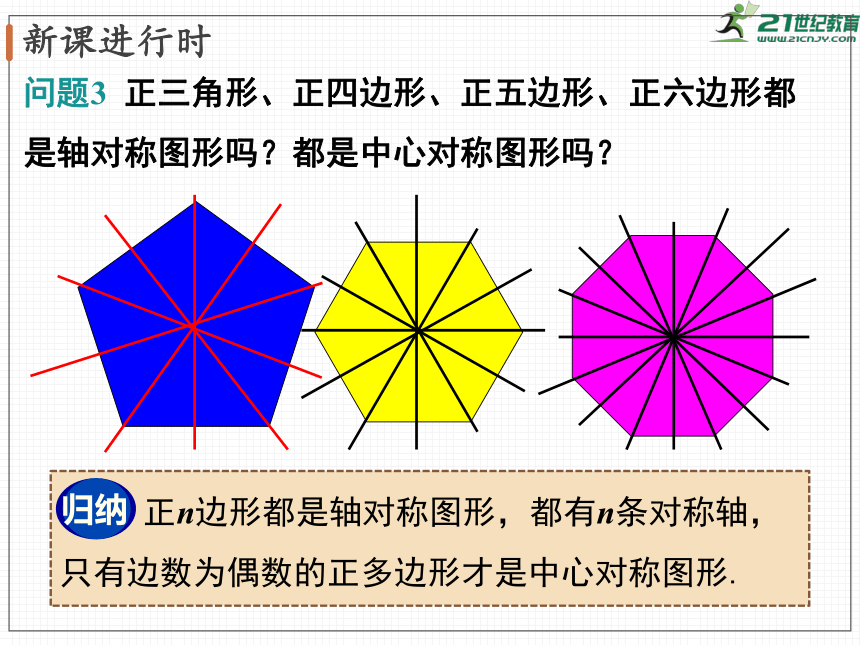
问题3
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形才是中心对称图形.
问题1
问题3
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
归纳
新课进行时
探究归纳
问题1
如图,把⊙O分成相等的5段弧,即AB=BC=CD=DE=EA,依次连接各等分点,所得五边形ABCDE是正五边形吗?
⌒
⌒
⌒
⌒
⌒
·
A
B
C
D
E
O
∴
同理
∴
解:
AB=BC=CD=DE=EA.
∠B=∠C=∠D=∠E.
∠A=∠B.
∴
五边形ABCDE是正五边形.
∵
AB=BC=CD=DE=EA
⌒
⌒
⌒
⌒
⌒
∴
BCE=CDA=3AB
⌒
⌒
⌒
新课进行时
核心知识点二
正多边形与圆的关系
弦相等(多边形的边相等)
圆周角相等(多边形的角相等)
—多边形是正多边形
问题2
将圆n(n≥3)等分,依次连接各等分点,所得到的多边形是正多边形吗?
弧相等—
将一个圆n(n≥3)等分,依次连接各等分点所得到的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆,正n边形的各顶点n等分其外接圆.
归纳
新课进行时
已知⊙O的半径为r,求作⊙O的内接正六边形.
分析:因为正六边形每条边所对的圆心角为
__
,
所以正六边形的边长与圆的半径
_
.
因此,在半径为r的圆上依次截取等于
的弦,
即可将圆六等分.
60?
相等
r
.
O
做一做
新课进行时
作法:(1)作⊙O的任意一条直径FC;
(2)分别以F,C为圆心,以r为半径作弧,与⊙O
交于点E,A和D,B;
(3)依次连接AB、BC、CD、DE、EF、FA,便
得到正六边形ABCDEF即为所求.
.
O
F
C
A
B
D
E
新课进行时
O
C
D
A
B
M
半径R
圆心角
弦心距r
弦a
圆心
中心角
A
B
C
D
E
F
O
半径R
边心距r
中心
类比学习
圆内接正多边形
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
弦心距
正多边形的边心距
M
核心知识点三
正多边形的有关概念及性质
新课进行时
中心角
A
B
C
D
E
F
O
半径R
边心距r
中心
正多边
形边数
内角
中心角
外角
3
4
6
n
60
°
120
°
120
°
90
°
90
°
90
°
120
°
60
°
60
°
正多边形的外角=中心角
练一练
完成下面的表格:
新课进行时
想一想
问题4
正n边形的中心角怎么计算?
C
D
O
B
E
F
A
P
问题5
正n边形的边长a,半径R,边心距r之间有什么关系?
a
R
r
问题6
边长a,边心距r的正n边形的面积如何计算?
其中l为正n边形的周长.
新课进行时
核心知识点四
圆内接正多边形的有关计算
例1:如图,正五边形ABCDE内接于⊙O,则∠ADE的度数是
(
)
A.60°
B.45°
C.
36°
D.
30°
·
A
B
C
D
E
O
典例精析
C
新课进行时
例2
有一个亭子,它的地基是半径为4
m的正六边形,求地基的周长和面积
(精确到0.1
m2).
C
D
O
E
F
A
P
抽象成
典例精析
B
新课进行时
利用勾股定理,可得边心距
亭子地基的面积
4m
O
A
B
C
D
E
F
M
r
解:过点O作OM⊥BC于M.
在Rt△OMB中,OB=4,MB=
亭子地基的周长l=6×4=24(m)
新课进行时
2.作边心距,构造直角三角形.
1.连半径,得中心角;
O
A
B
C
D
E
F
R
M
r
·
圆内接正多边形的辅助线
方法归纳
O
边心距r
边长一半
半径R
C
M
中心角一半
新课进行时
1.如图,正八边形ABCDEFGH的半径为2,它的面积为______.
解:连接AO,BO,CO,AC,
∵正八边形ABCDEFGH的半径为2,
∴AO=BO=CO=2,∠AOB=∠BOC=
,
∴∠AOC=90°,
∴AC=
,此时AC与BO垂直,
∴S四边形AOCB=
,
∴正八边形面积为:
.
新课进行时
知识小结
4
知识小结
圆内接正多边形
正多边形和圆的关系
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正n边形各顶点等分其外接圆.
随堂演练
5
随堂演练
正多边形边数
半径
边长
边心距
周长
面积
3
4
1
6
1.
填表
2
1
2
8
4
2
2
12
2.
若正多边形的边心距与半径的比为1:2,则这个多边形的边数是
.
3
3.已知一个正多边形的每个内角均为108°,则它的中心角为________度.
72
4.下列说法正确的是(
)
A.各边都相等的多边形是正多边形
B.一个圆有且只有一个内接正多边形
C.圆内接正四边形的边长等于半径
D.圆内接正n边形的中心角度数为
D
随堂演练
6.
要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
也就是要找这个正方形外接圆的直径
5.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为
___度.(不取近似值)
随堂演练
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第三章
圆
3.8
圆内接正多边形
北师大版
九年级数学下册
教学课件
目录
1
新课目标
新课进行时
3
2
情景导学
知识小结
4
CONTENTS
随堂演练
5
课后作业
6
新课目标
1
新课目标
【知识与技能】
1.掌握圆内接正多边形、外接圆、边心距、中心角的概念.
2.正多边形的画法.
【过程与方法】
通过作图的过程,提高学生的几何语言表达能力和合情推理能力.
【情感态度】
在学生动手操作的过程中,增强学生的数学应用意识,提高学生学习数学的兴趣和积极性,培养学生主动探索的精神,培养学生合作交流和创新意识.
【教学重点】
圆内接正多边形、外接圆、边心距、中心角的概念.
【教学难点】
圆内接正多边形、外接圆、边心距、中心角的概念.
情景导学
2
情景导学
问题:观看大屏幕上这些美丽的图案,都是在日常生活中我们经常能看到的.你能从这些图案中找出类似的图形吗?
观察与思考
新课进行时
3
新课进行时
核心知识点一
正多边形的回顾
问题1
什么叫做正多边形?
各边相等,各角也相等的多边形叫做正多边形.
问题2
矩形是正多边形吗?为什么?菱形是正多边形吗?为什么?
不是,因为矩形不符合各边相等;
不是,因为菱形不符合各角相等;
注意
正多边形
各边相等
各角相等
缺一不可
新课进行时
问题3
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
正n边形都是轴对称图形,都有n条对称轴,只有边数为偶数的正多边形才是中心对称图形.
问题1
问题3
正三角形、正四边形、正五边形、正六边形都是轴对称图形吗?都是中心对称图形吗?
归纳
新课进行时
探究归纳
问题1
如图,把⊙O分成相等的5段弧,即AB=BC=CD=DE=EA,依次连接各等分点,所得五边形ABCDE是正五边形吗?
⌒
⌒
⌒
⌒
⌒
·
A
B
C
D
E
O
∴
同理
∴
解:
AB=BC=CD=DE=EA.
∠B=∠C=∠D=∠E.
∠A=∠B.
∴
五边形ABCDE是正五边形.
∵
AB=BC=CD=DE=EA
⌒
⌒
⌒
⌒
⌒
∴
BCE=CDA=3AB
⌒
⌒
⌒
新课进行时
核心知识点二
正多边形与圆的关系
弦相等(多边形的边相等)
圆周角相等(多边形的角相等)
—多边形是正多边形
问题2
将圆n(n≥3)等分,依次连接各等分点,所得到的多边形是正多边形吗?
弧相等—
将一个圆n(n≥3)等分,依次连接各等分点所得到的多边形叫作这个圆的内接正多边形,这个圆是这个正多边形的外接圆,正n边形的各顶点n等分其外接圆.
归纳
新课进行时
已知⊙O的半径为r,求作⊙O的内接正六边形.
分析:因为正六边形每条边所对的圆心角为
__
,
所以正六边形的边长与圆的半径
_
.
因此,在半径为r的圆上依次截取等于
的弦,
即可将圆六等分.
60?
相等
r
.
O
做一做
新课进行时
作法:(1)作⊙O的任意一条直径FC;
(2)分别以F,C为圆心,以r为半径作弧,与⊙O
交于点E,A和D,B;
(3)依次连接AB、BC、CD、DE、EF、FA,便
得到正六边形ABCDEF即为所求.
.
O
F
C
A
B
D
E
新课进行时
O
C
D
A
B
M
半径R
圆心角
弦心距r
弦a
圆心
中心角
A
B
C
D
E
F
O
半径R
边心距r
中心
类比学习
圆内接正多边形
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
弦心距
正多边形的边心距
M
核心知识点三
正多边形的有关概念及性质
新课进行时
中心角
A
B
C
D
E
F
O
半径R
边心距r
中心
正多边
形边数
内角
中心角
外角
3
4
6
n
60
°
120
°
120
°
90
°
90
°
90
°
120
°
60
°
60
°
正多边形的外角=中心角
练一练
完成下面的表格:
新课进行时
想一想
问题4
正n边形的中心角怎么计算?
C
D
O
B
E
F
A
P
问题5
正n边形的边长a,半径R,边心距r之间有什么关系?
a
R
r
问题6
边长a,边心距r的正n边形的面积如何计算?
其中l为正n边形的周长.
新课进行时
核心知识点四
圆内接正多边形的有关计算
例1:如图,正五边形ABCDE内接于⊙O,则∠ADE的度数是
(
)
A.60°
B.45°
C.
36°
D.
30°
·
A
B
C
D
E
O
典例精析
C
新课进行时
例2
有一个亭子,它的地基是半径为4
m的正六边形,求地基的周长和面积
(精确到0.1
m2).
C
D
O
E
F
A
P
抽象成
典例精析
B
新课进行时
利用勾股定理,可得边心距
亭子地基的面积
4m
O
A
B
C
D
E
F
M
r
解:过点O作OM⊥BC于M.
在Rt△OMB中,OB=4,MB=
亭子地基的周长l=6×4=24(m)
新课进行时
2.作边心距,构造直角三角形.
1.连半径,得中心角;
O
A
B
C
D
E
F
R
M
r
·
圆内接正多边形的辅助线
方法归纳
O
边心距r
边长一半
半径R
C
M
中心角一半
新课进行时
1.如图,正八边形ABCDEFGH的半径为2,它的面积为______.
解:连接AO,BO,CO,AC,
∵正八边形ABCDEFGH的半径为2,
∴AO=BO=CO=2,∠AOB=∠BOC=
,
∴∠AOC=90°,
∴AC=
,此时AC与BO垂直,
∴S四边形AOCB=
,
∴正八边形面积为:
.
新课进行时
知识小结
4
知识小结
圆内接正多边形
正多边形和圆的关系
正多边形的
有关概念
正多边形的
有关计算
添加辅助线的方法:
连半径,作边心距
中心
半径
边心距
中心角
正n边形各顶点等分其外接圆.
随堂演练
5
随堂演练
正多边形边数
半径
边长
边心距
周长
面积
3
4
1
6
1.
填表
2
1
2
8
4
2
2
12
2.
若正多边形的边心距与半径的比为1:2,则这个多边形的边数是
.
3
3.已知一个正多边形的每个内角均为108°,则它的中心角为________度.
72
4.下列说法正确的是(
)
A.各边都相等的多边形是正多边形
B.一个圆有且只有一个内接正多边形
C.圆内接正四边形的边长等于半径
D.圆内接正n边形的中心角度数为
D
随堂演练
6.
要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
也就是要找这个正方形外接圆的直径
5.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为
___度.(不取近似值)
随堂演练
课后作业
6
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
