简单的线性规划问题
图片预览



文档简介
(共26张PPT)
简单的线性规划问题
O
x
y
3
5
复习判断二元一次不等式表示哪一侧平面区域的方法
O
x
y
1
1
x+y-1=0
x+y-1>0
x+y-1<0
由于对在直线ax+by+c=0同
一侧所有点(x,y),把它的坐标
(x,y)代入ax+by+c,所得的实
数的符号都相同,故只需在这条
直线的某一侧取一特殊点(x0,y0)
以ax0+by0+c的正负的情况便可
判断ax+by+c>0表示这一直线
哪一侧的平面区域,特殊地,当
c≠0时常把原点作为此特殊点
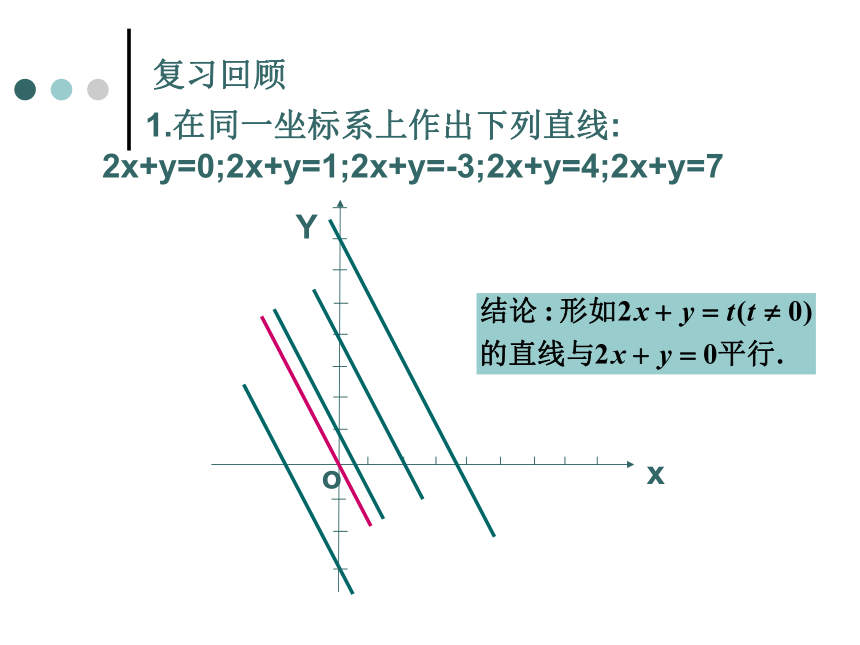
复习回顾
1.在同一坐标系上作出下列直线:
2x+y=0;2x+y=1;2x+y=-3;2x+y=4;2x+y=7
x
Y
o
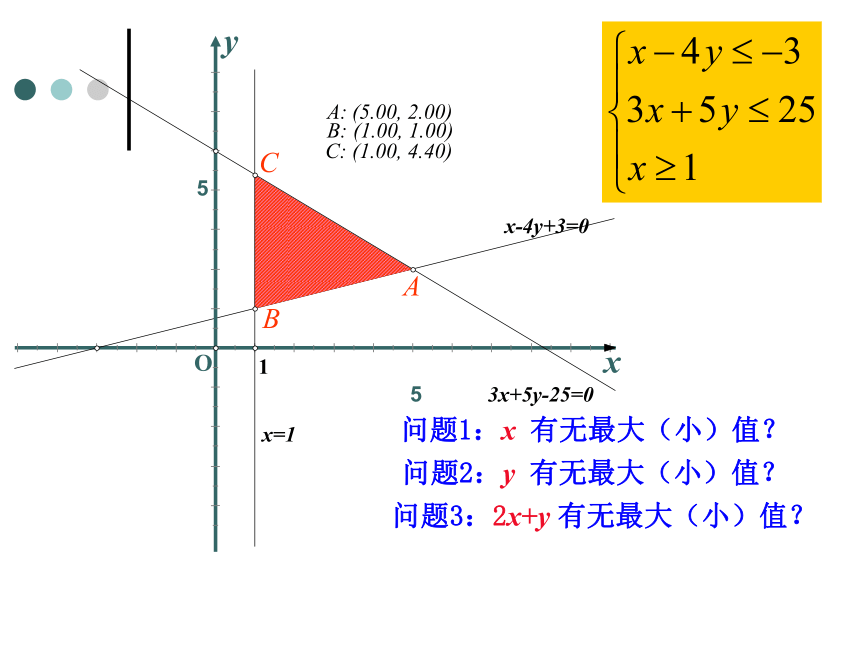
2.作出下列不等式组的所表示的平面区域
5
5
x=1
x-4y+3=0
3x+5y-25=0
1
A
B
C
C:
(1.00, 4.40)
A:
(5.00, 2.00)
B:
(1.00, 1.00)
O
x
y
问题1:x 有无最大(小)值?
问题2:y 有无最大(小)值?
问题3:2x+y 有无最大(小)值?
二.提出问题
把上面两个问题综合起来:
设z=2x+y,求满足
时,z的最大值和最小值.
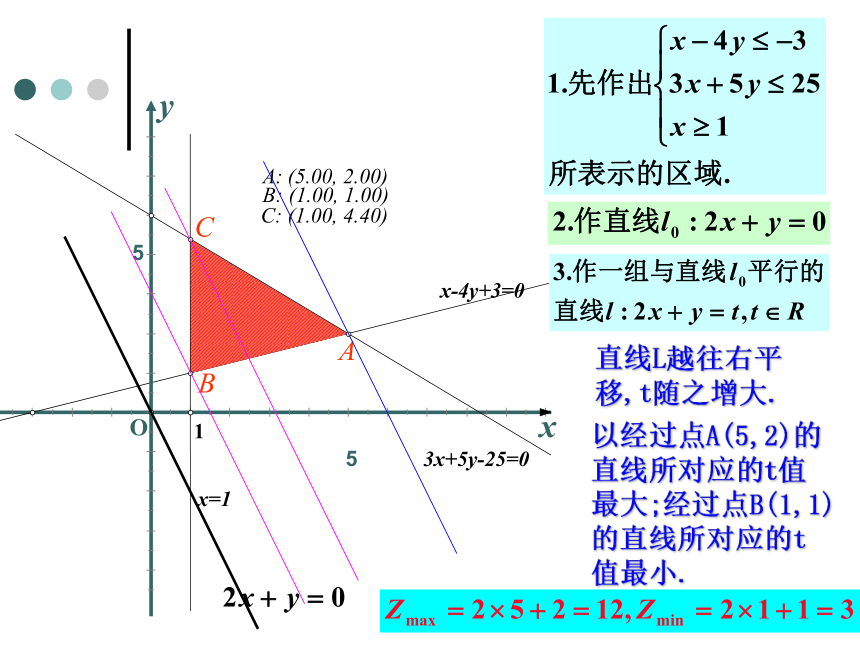
5
5
x=1
x-4y+3=0
3x+5y-25=0
1
A
B
C
C:
(1.00, 4.40)
A:
(5.00, 2.00)
B:
(1.00, 1.00)
O
x
y
直线L越往右平移,t随之增大.
以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.
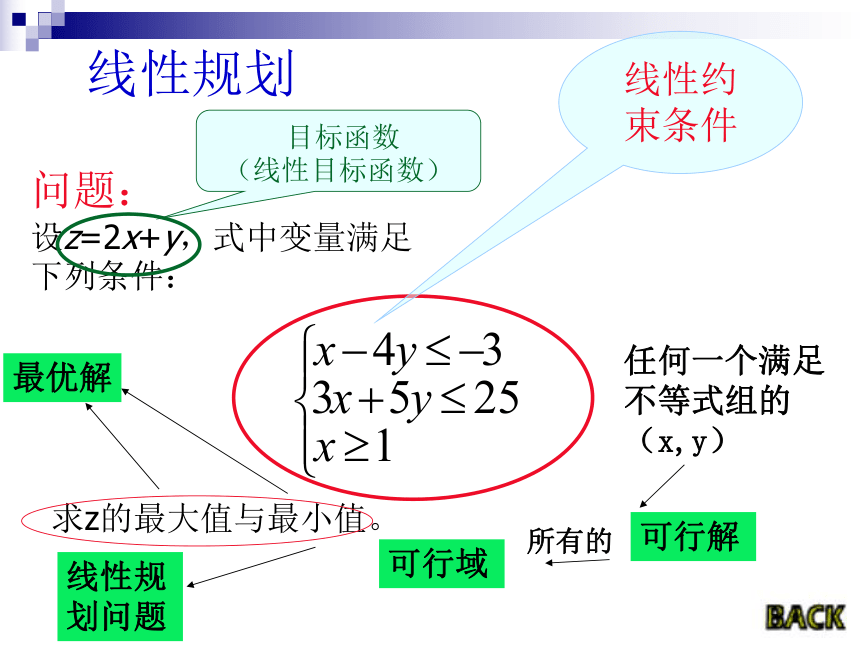
线性规划
问题:
设z=2x+y,式中变量满足
下列条件:
求z的最大值与最小值。
目标函数
(线性目标函数)
线性约
束条件
任何一个满足不等式组的(x,y)
可行解
可行域
所有的
最优解
线性规划问题
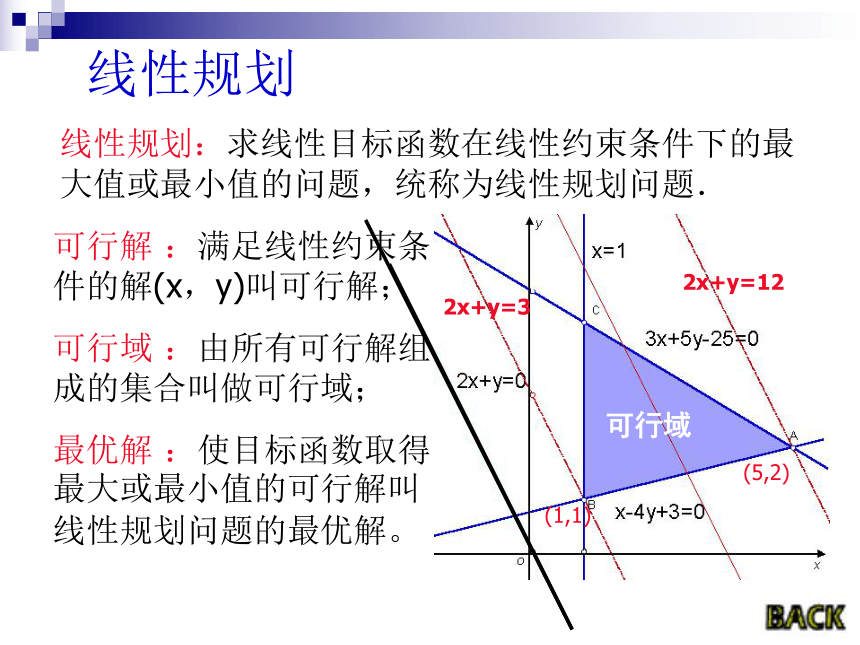
线性规划
线性规划:求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.
可行解 :满足线性约束条件的解(x,y)叫可行解;
可行域 :由所有可行解组成的集合叫做可行域;
最优解 :使目标函数取得最大或最小值的可行解叫线性规划问题的最优解。
可行域
2x+y=3
2x+y=12
(1,1)
(5,2)
线性规划
练习1: 解下列线性规划问题:
求z=2x+y的最大值和最小值,使式中x、y满足下
列条件:
探索结论
2x+y=0
2x+y=-3
2x+y=3
答案:当x=-1,y=-1时,z=2x+y有最小值-3.
当x=2,y=-1时,z=2x+y有最大值3.
线性规划
例2 解下列线性规划问题:
求z=300x+900y的最大值和最小值,使式中x、y满足下列条件:
探索结论
x+3y=0
300x+900y=0
300x+900y=112500
答案:当x=0,y=0时,z=300x+900y有最小值0.
当x=0,y=125时,z=300x+900y有最大值112500.
解线性规划问题的步骤:
(2)移:在线性目标函数所表示的一组平行 线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
(3)求:通过解方程组求出最优解;
(4)答:作出答案。
(1)画:画出线性约束条件所表示的可行域;
总结
几个结论:
1、线性目标函数的最大(小)值一般在可行域的顶点处取得,也可能在边界处取得。
2、求线性目标函数的最优解,要注意分析线性目标函数所表示的几何意义 ——在y轴上的截距或其相反数。
课本91页练习 1(1)
课本91页练习 2
例5 营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1kg食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?
食物/kg 碳水化合物/kg 蛋白质/kg 脂肪/kg
A 0.105 0.07 0.14
B 0.105 0.14 0.07
将已知数据列表得
解:设每天食用xkg食物A,ykg食物B,总成本为z,那么
解:设每天食用xkg食物A,ykg食物B,总成本为z,那么
目标函数为z=28x+21y
作出二元一次不等式组所表示的可行域,如图:
目标函数为z=28x+21y
答:每天食用食物A约143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元.
例2 要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 :
解:设需截第一种钢板x张,第一种钢板y张,一共使用z张. 则
规格类型
钢板类型
第一种钢板
第二种钢板
A规格
B规格
C规格
2
1
2
1
3
1
作出可行域(如图)
目标函数为 z=x+y
今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。
2x+y=15
x+3y=27
x+2y=18
x+y =0
2x+y≥15,
{
x+2y≥18,
x+3y≥27,
x≥0, x∈N*
y≥0 y∈N*
直线x+y=12经过的整点是B(3,9)和C(4,8),它们是最优解.
答:(略)
作出一组平行直线z = x+y,
目标函数z = x+y
B(3,9)
C(4,8)
M(18/5,39/5)
调整优值法
作直线x+y=12
当直线经过点M时z=x+y=11.4,但它不是最优整数解,
解得交点B,C的坐标B(3,9)和C(4,8)
x
0
y
2x+y=15
x+3y=27
x+2y=18
x+y =0
经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.
答:(略)
作出一组平行直线z = x+y,
目标函数z = x+y
B(3,9)
C(4,8)
M(18/5,39/5)
打网格线法
在可行域内打出网格线,
当直线经过点M时z=x+y=11.4,但它不是最优整数解,
将直线x+y=11.4继续向上平移,
x
0
y
简单的线性规划问题
O
x
y
3
5
复习判断二元一次不等式表示哪一侧平面区域的方法
O
x
y
1
1
x+y-1=0
x+y-1>0
x+y-1<0
由于对在直线ax+by+c=0同
一侧所有点(x,y),把它的坐标
(x,y)代入ax+by+c,所得的实
数的符号都相同,故只需在这条
直线的某一侧取一特殊点(x0,y0)
以ax0+by0+c的正负的情况便可
判断ax+by+c>0表示这一直线
哪一侧的平面区域,特殊地,当
c≠0时常把原点作为此特殊点
复习回顾
1.在同一坐标系上作出下列直线:
2x+y=0;2x+y=1;2x+y=-3;2x+y=4;2x+y=7
x
Y
o
2.作出下列不等式组的所表示的平面区域
5
5
x=1
x-4y+3=0
3x+5y-25=0
1
A
B
C
C:
(1.00, 4.40)
A:
(5.00, 2.00)
B:
(1.00, 1.00)
O
x
y
问题1:x 有无最大(小)值?
问题2:y 有无最大(小)值?
问题3:2x+y 有无最大(小)值?
二.提出问题
把上面两个问题综合起来:
设z=2x+y,求满足
时,z的最大值和最小值.
5
5
x=1
x-4y+3=0
3x+5y-25=0
1
A
B
C
C:
(1.00, 4.40)
A:
(5.00, 2.00)
B:
(1.00, 1.00)
O
x
y
直线L越往右平移,t随之增大.
以经过点A(5,2)的直线所对应的t值最大;经过点B(1,1)的直线所对应的t值最小.
线性规划
问题:
设z=2x+y,式中变量满足
下列条件:
求z的最大值与最小值。
目标函数
(线性目标函数)
线性约
束条件
任何一个满足不等式组的(x,y)
可行解
可行域
所有的
最优解
线性规划问题
线性规划
线性规划:求线性目标函数在线性约束条件下的最大值或最小值的问题,统称为线性规划问题.
可行解 :满足线性约束条件的解(x,y)叫可行解;
可行域 :由所有可行解组成的集合叫做可行域;
最优解 :使目标函数取得最大或最小值的可行解叫线性规划问题的最优解。
可行域
2x+y=3
2x+y=12
(1,1)
(5,2)
线性规划
练习1: 解下列线性规划问题:
求z=2x+y的最大值和最小值,使式中x、y满足下
列条件:
探索结论
2x+y=0
2x+y=-3
2x+y=3
答案:当x=-1,y=-1时,z=2x+y有最小值-3.
当x=2,y=-1时,z=2x+y有最大值3.
线性规划
例2 解下列线性规划问题:
求z=300x+900y的最大值和最小值,使式中x、y满足下列条件:
探索结论
x+3y=0
300x+900y=0
300x+900y=112500
答案:当x=0,y=0时,z=300x+900y有最小值0.
当x=0,y=125时,z=300x+900y有最大值112500.
解线性规划问题的步骤:
(2)移:在线性目标函数所表示的一组平行 线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线;
(3)求:通过解方程组求出最优解;
(4)答:作出答案。
(1)画:画出线性约束条件所表示的可行域;
总结
几个结论:
1、线性目标函数的最大(小)值一般在可行域的顶点处取得,也可能在边界处取得。
2、求线性目标函数的最优解,要注意分析线性目标函数所表示的几何意义 ——在y轴上的截距或其相反数。
课本91页练习 1(1)
课本91页练习 2
例5 营养学家指出,成人良好的日常饮食应该至少提供0.075kg的碳水化合物,0.06kg的蛋白质,0.06kg的脂肪,1kg食物A含有0.105kg碳水化合物,0.07kg蛋白质,0.14kg脂肪,花费28元;而1kg食物B含有0.105kg碳水化合物,0.14kg蛋白质,0.07kg脂肪,花费21元。为了满足营养专家指出的日常饮食要求,同时使花费最低,需要同时食用食物A和食物B多少kg?
食物/kg 碳水化合物/kg 蛋白质/kg 脂肪/kg
A 0.105 0.07 0.14
B 0.105 0.14 0.07
将已知数据列表得
解:设每天食用xkg食物A,ykg食物B,总成本为z,那么
解:设每天食用xkg食物A,ykg食物B,总成本为z,那么
目标函数为z=28x+21y
作出二元一次不等式组所表示的可行域,如图:
目标函数为z=28x+21y
答:每天食用食物A约143g,食物B约571g,能够满足日常饮食要求,又使花费最低,最低成本为16元.
例2 要将两种大小不同规格的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示 :
解:设需截第一种钢板x张,第一种钢板y张,一共使用z张. 则
规格类型
钢板类型
第一种钢板
第二种钢板
A规格
B规格
C规格
2
1
2
1
3
1
作出可行域(如图)
目标函数为 z=x+y
今需要A,B,C三种规格的成品分别为15,18,27块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少。
2x+y=15
x+3y=27
x+2y=18
x+y =0
2x+y≥15,
{
x+2y≥18,
x+3y≥27,
x≥0, x∈N*
y≥0 y∈N*
直线x+y=12经过的整点是B(3,9)和C(4,8),它们是最优解.
答:(略)
作出一组平行直线z = x+y,
目标函数z = x+y
B(3,9)
C(4,8)
M(18/5,39/5)
调整优值法
作直线x+y=12
当直线经过点M时z=x+y=11.4,但它不是最优整数解,
解得交点B,C的坐标B(3,9)和C(4,8)
x
0
y
2x+y=15
x+3y=27
x+2y=18
x+y =0
经过可行域内的整点B(3,9)和C(4,8)且和原点距离最近的直线是x+y=12,它们是最优解.
答:(略)
作出一组平行直线z = x+y,
目标函数z = x+y
B(3,9)
C(4,8)
M(18/5,39/5)
打网格线法
在可行域内打出网格线,
当直线经过点M时z=x+y=11.4,但它不是最优整数解,
将直线x+y=11.4继续向上平移,
x
0
y
