一元二次不等式及其解法

(共29张PPT)
课题:一元二次不等式解法(一)
一元二次不等式及其解法
复习：一元二次方程与一元二次函数
(1)一元二次方程的解法
因式分解法(十字相乘）
公式法：
(2)一元二次函数
开口方向；
对称轴
顶点 坐标
例如下面的不等式：
15x2+30x－1>0 和 3x2+6x－1≤0.
一元二次不等式有两个共同特点：
（1）含有一个未知数x；
（2）未知数的最高次数为2.
一般地，含有一个未知数，且未知数的最高次数为2的整式不等式，叫做一元二次不等式。
问题：如何解一元二次不等式呢？
考察：对一次函数y=2x-7，当x为何值时，y=0;当x为何值时，y<0;当x为何值时，y>0？
当x=3.5时，2x-7=0，
即 y=0；
当x<3.5时，2x-7<0，
即 y<0；
当x>3.5时，2x-7>0，
即 y>0
O
y
x
3.5
O
y
x
m
O
y
x
n
想一想，当x取何值时，y 的值大于零？（或小于零？）
O
y
x
3
-2
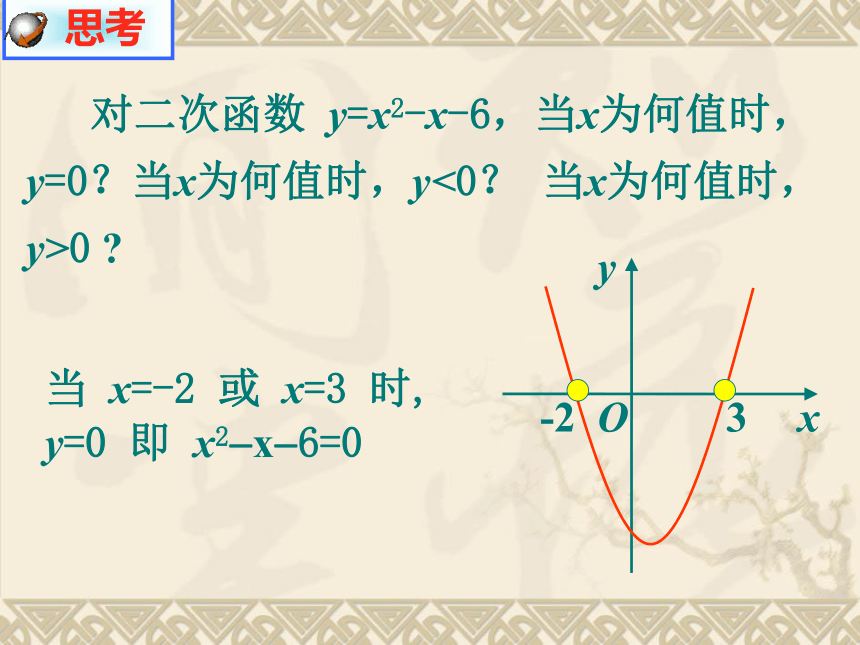
对二次函数 y=x2-x-6，当x为何值时，y=0？当x为何值时，y<0？ 当x为何值时，y>0
思考
当 x=-2 或 x=3 时, y=0 即 x2 x 6=0
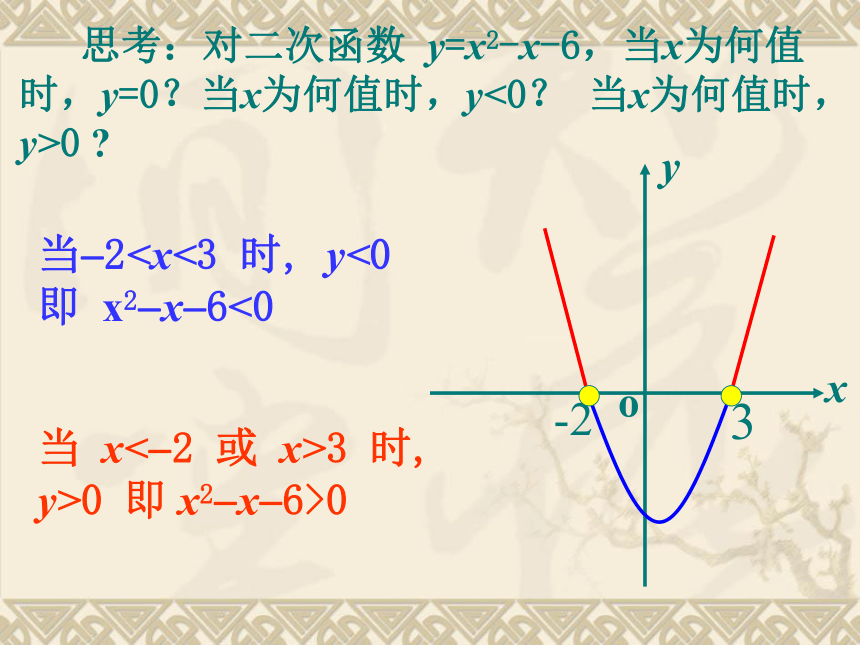
思考：对二次函数 y=x2-x-6，当x为何值时，y=0？当x为何值时，y<0？ 当x为何值时，y>0
当 x< 2 或 x>3 时, y>0 即 x2 x 6>0
当 2o
x
y
3
-2
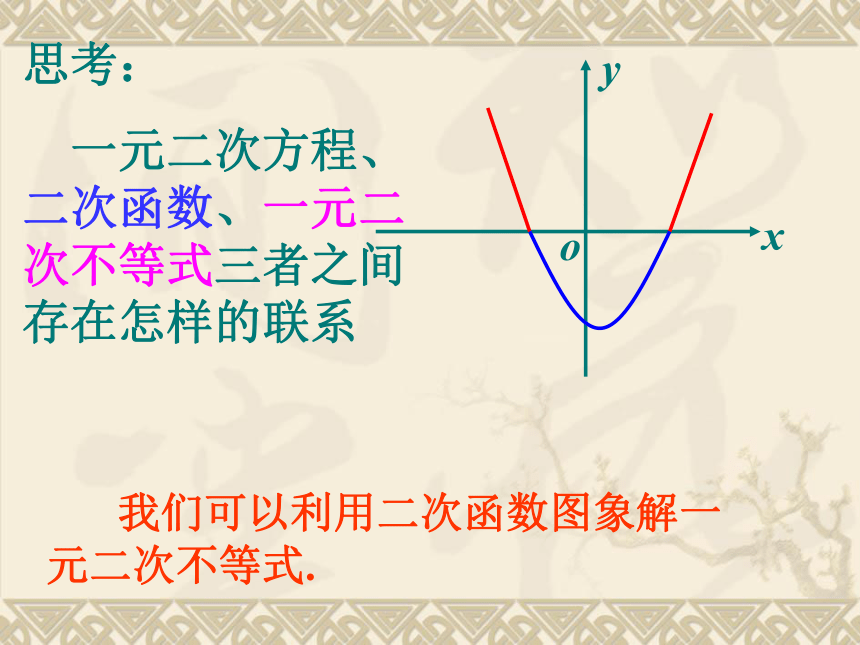
思考：
一元二次方程、二次函数、一元二次不等式三者之间存在怎样的联系
o
x
y
我们可以利用二次函数图象解一元二次不等式.
O
y
x
3
-2
若一元二次方程x2-x-6=0
的解是x1=-2，x2=3.
则抛物线y=x2-x-6与
x轴的交点就是
(-2，0)与(3，0),
一元二次不等式
x2-x-6<0 的解集是 {x|-2x2-x-6>0 的解集是 {x|x<-2或x>3}.
y=x2-x-6
问：二次函数y= ax2＋bx＋c（a>0）
与x轴的交点情况有哪几种？
Δ>0 Δ=0 Δ<0
O
y
x
x1
x2
x1=x2
利用二次函数图象能解一元二次不等式！
=
=
<
<
>
>
练习.解不等式 2x2－3x－2 > 0 .
解:因为△ =(-3)2-4×2×(-2)>0,
所以方程2x2－3x－2 =0的解是
所以,原不等式的解集是
先求方程的根
然后想像图象形状
若改为:不等式 2x2－3x－2 < 0 .
总结: 解一元二次不等式 ax2+bx+c>0 (a>0，△≥0 )的步骤：
① 将二次不等式化成一般式（a>0 ）；
② 求出方程ax2+bx+c=0的两根;
④ 根据图象写出不等式的解集.
③ 画出y=ax2+bx+c的图象;
思考：
如何求一元二次
不等式x2-7x+6 > 0
的解集
(-∞，1）
（1，6）
（6，+∞）
小于取中间
x
y
y=x2-7x+6
大于取两边
判别式
△=b2- 4ac
y=ax2+bx+c
(a>0)的图象
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
△>0
有两相异实根
x1, x2 (x1{x|xx2}
{x|x1< x △=0
△<0
有两相等实根
x1=x2=
{x|x≠ }
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
这张表是我们今后求解一元二次不等式的主要工具，必须熟练掌握，其关键是抓住相应的二次函数的图像。
记忆口诀：
大于取两边，小于取中间.
求解一元二次不等式ax2+bx+c>0
(a>0)的程序框图（课本87页）:
△≥0
x< x1或x> x2
例1.解不等式 4x2－4x＋1 > 0
解:因为△ =0,方程4x2－4x＋1 =0的解是
所以,原不等式的解集是
注:4x2－4x＋1 <0
无解
例2、－x2 ＋2x -3＞0
x
o
y
－x2 ＋2x －3＞0图象如右图：
x
o
y
再次强调注意公式口诀的大前提： a>0
课本80页 练习 1（1）（2）（3）
课本80页 A 1（2）（3）（4）
课本80页 A 2（2）
课本80页 A 3,4
解：设这辆车刹车前的车速至少为xkm/h，根据题意，我们得到
移项整理，得
例3、某种汽车在水泥路面上的刹车距离s(米)和汽车车速x(千米/小时)有如下关系，
在一次交通事故测得这种车的刹车距离大于39.5m，那么这辆车刹车前的车速至少是多少？(精确到0.01km/h)
在这个实际问题中，x>0,所以这辆车刹车的车速至少为79.94km/h。
例3、某种汽车在水泥路面上的刹车距离s(米)和汽车车速x(千米/小时)有如下关系，
在一次交通事故测得这种车的刹车距离大于39.5m，那么这辆车刹车前的车速至少是多少？(精确到0.01km/h)
移项整理，得
例4 一个车辆制造厂引进了一条摩托车整车装配流水线,这条流水线生产的摩托车数量x(辆)与创造的价值 y(元)之间有如下的关系: y = -2 x2 + 220x. 若这家工厂希望在一个星期内利用这条流水线创收6000元以上,那么它在一个星期内大约应该生产多少辆摩托车
解:设在一个星期内大约应该生产x辆摩托车.根据题意,得到 -2x2 + 220x > 6000
移项整理,得 x2 - 110x + 3000 < 0.
因为△=100>0,所以方程 x2-110x+3000=0有两个实数根x1=50, x2=60.
解:设在一个星期内大约应该生产x辆摩托车.根据题意,得到 -2x2 + 220x > 6000
移项整理,得 x2 - 110x + 3000 < 0.
因为△=100>0,所以方程 x2-110x+3000=0有两个实数根
x1=50, x2=60.
由函数y=x2-110x+3000的图象,
得不等式的解为50因为x只能取整数,所以当这条摩托
车整车装配流水线在一周内生产的摩托
车数量在51辆到59辆之间时,这家工厂
能够获得6000元以上的收益.