人教版数学九年级上册 24.2.2 直线和圆的位置关系 同步练习(共3课时 word版 含答案)
文档属性
| 名称 | 人教版数学九年级上册 24.2.2 直线和圆的位置关系 同步练习(共3课时 word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 264.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 08:39:08 | ||
图片预览




文档简介
24.2.2 直线和圆的位置关系
第1课时 直线和圆的位置关系
1.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为( )
A.相离 B.相切 C.相交 D.无法确定
2.已知一条直线与圆有公共点,则这条直线与圆的位置关系是( )
A.相离 B.相切 C.相交 D.相切或相交
3.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
A.相离 B.相交
C.相切 D.以上三种情况均有可能
4.⊙O的半径为6,一条弦长6,以3为半径的同心圆与这条弦的关系是( )
A.相切 B.相交
C.相离 D.相切或相交
5.在Rt△ABC中,∠C=90°,AB=4 cm,BC=2 cm,以C为圆心,r为半径的圆与AB有何种位置关系?请你写出判断过程.
(1)r=1.5 cm;(2)r= cm;(3)r=2 cm.
6.设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d的取值范围为( )
A.d≤4 B.d<4 C.d≥4 D.d=4
7.如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1 B.1或5 C.3 D.5
8.⊙O的半径为R,点O到直线l的距离为d,R,d是方程x2-4x+m=0的两根,当直线l与⊙O相切时,m的值为 .
9.如图,在Rt△ABC中,∠A=90°,∠C=60°,BO=x,⊙O的半径为2,当x在什么范围内取值时,AB所在的直线与⊙O相交、相切、相离?
10.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是
11.如图,⊙O的半径OC=5 cm,直线l⊥OC,垂足为H,且l交⊙O于A,B两点,AB=8 cm.若l沿OC所在直线平移与⊙O相切,则平移的距离是 .
12.如图,在Rt△ABC中,∠B=90°,∠A=60°,BC=4 cm,以B为圆心,2 cm长为半径作圆,则⊙B与AC的位置关系是( )
A.相离 B.相切 C.相交 D.外切
13.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.-2≤b≤2
C.-214.已知如图,∠BOA=30°,M是OB上一点,以M为圆心、2 cm为半径作⊙M,点M在射线OB上运动,当OM=5 cm时,⊙M与直线OA的位置关系是 .
15. 如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于点N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上,则以MN为直径的圆与直线AB的位置关系是
16.如图所示,半径为2的⊙P的圆心在直线y=2x-1上运动.
(1)当⊙P和x轴相切时,写出点P的坐标;并判断此时y轴与⊙P的位置关系;
(2)当⊙P和y轴相切时,写出点P的坐标;并判断此时x轴与⊙P的位置关系;
(3)⊙P是否能同时与x轴和y轴相切?若能,写出点P的坐标;若不能,说明理由.
17.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m= ;
(2)当m=2时,d的取值范围是 .
第2课时 切线的判定与性质
1.下列说法中,正确的是( )
A.AB垂直于⊙O的半径,则AB是⊙O的切线
B.经过半径外端的直线是圆的切线
C.经过切点的直线是圆的切线
D.圆心到直线的距离等于半径,那么这条直线是圆的切线
2.如图,AB是半圆的直径,O为圆心,AD,BD是半圆的弦,且∠PDA=∠PBD.判断直线PD是否为⊙O的切线,并说明理由.
3.如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA=30°,则OB的长为( )
A.4 B.4 C.2 D.2
4.如图,已知直线AD是⊙O的切线,点A为切点,OD交⊙O于点B,点C在⊙O上,且∠ODA=36°,则∠ACB的度数为( )
A.54° B.36° C.30° D.27°
5.如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,PB=3,则⊙O的半径是( )
A.5 B.4 C.4.5 D.3.5
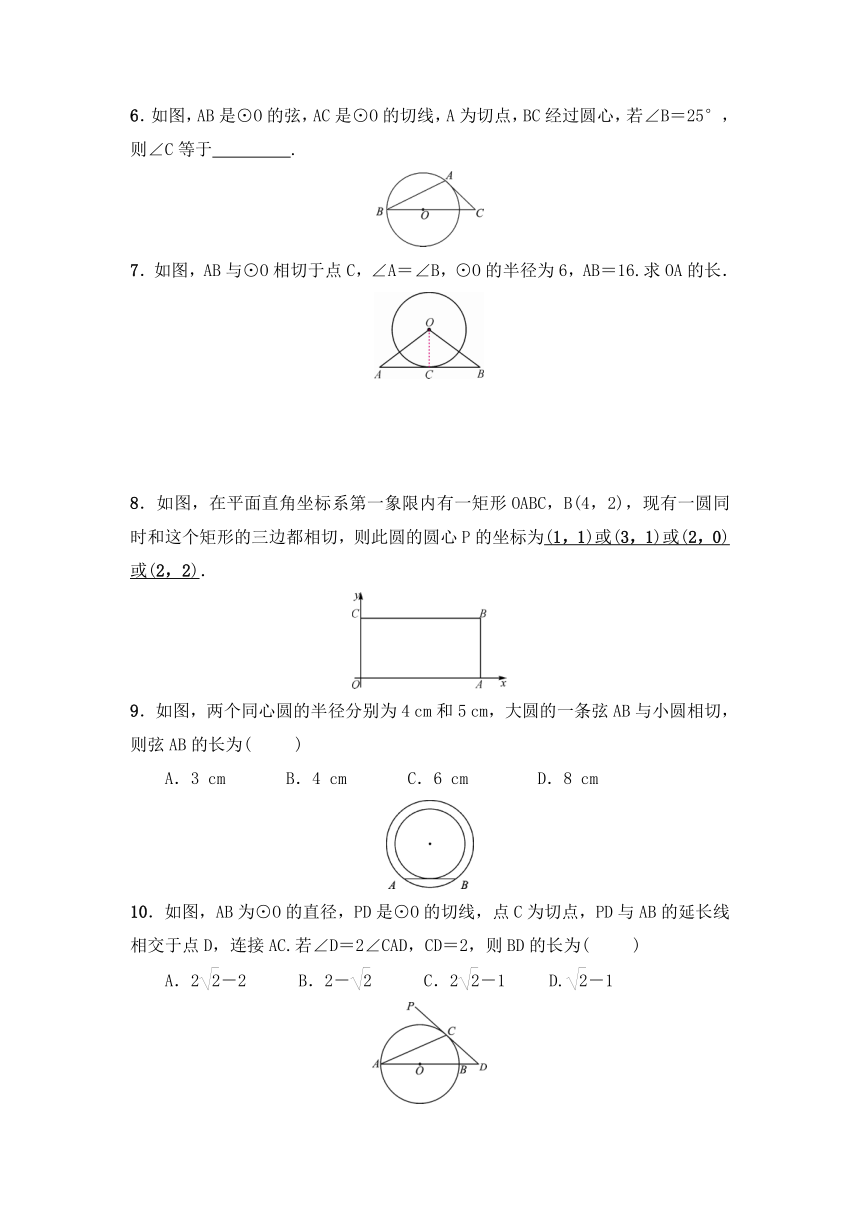
6.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C等于 .
7.如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16.求OA的长.
8.如图,在平面直角坐标系第一象限内有一矩形OABC,B(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心P的坐标为(1,1)或(3,1)或(2,0)或(2,2).
9.如图,两个同心圆的半径分别为4 cm和5 cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
A.3 cm B.4 cm C.6 cm D.8 cm
10.如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC.若∠D=2∠CAD,CD=2,则BD的长为( )
A.2-2 B.2- C.2-1 D.-1
11.如图,以△AOB的顶点O为圆心,OA为半径的⊙O交BO于点C,此时AB恰好与⊙O相切,P为⊙O上任意一点(不与A,C重合),已知BC=AO,则∠P= .
12. 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA,CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.
13.如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线;
(2)若∠A=30°,AC=6,求⊙O的周长.
14.如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.求证:∠1=∠2.
15.如图,等腰△ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
324612029210(1)求证:直线EF是⊙O的切线;
(2)求DF的值.
第3课时 切线长定理
1.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.4 D.8
2.如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
A.15° B.30° C.60° D.75°
3.如图,AB,AC,BD是⊙O的切线,P,C,D为切点,如果AB=5,AC=3,则BD的长为 .
4.如图,PA,PB是⊙O的切线,切点分别是A,B,若∠APB=60°,OA=2 cm,则OP= cm.
5.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若三角板与圆相切且测得PA=5 cm,求铁环的半径.
6.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
7.如图,△ABC中,AB=7 cm,AC=8 cm,BC=6 cm,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则△CEF的周长为 cm.
8.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC=26 cm,CA=28 cm,求AF,BD,CE的长.
9.如图,△ABC是圆的内接三角形,点P是△ABC的内心,∠A=50°,则∠BPC的度数为 .
10.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( )
A.9 B.10 C.12 D.14
11.如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6 m和8 m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
A.2 m B.3 m C.6 m D.9 m
12.如图,菱形ABCD的边长为10,⊙O分别与AB,AD相切于E,F两点,且与BG相切于点G.若AO=5,且⊙O的半径为3,则BG的长度为( )
A.4 B.5 C.6 D.7
13.如图,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在上,若PA长为2,则△PEF的周长为 .
14.如图所示,点I为△ABC的内心,点O为△ABC的外心,若∠BOC=140°,求∠BIC的度数.
15.如图,CD是⊙O的直径,且CD=2 cm,点P为CD的延长线上一点,过点P作⊙O的切线PA,PB,切点分别为点A,B.
(1)连接AC,若∠APO=30°,试证明△ACP是等腰三角形;
(2)填空:
①当DP=1cm时,四边形AOBD是菱形;
②当DP=(-1)cm时,四边形AOBP是正方形.
参考答案:
24.2.2 直线和圆的位置关系
第1课时 直线和圆的位置关系
1.C
2.D
3.C
4.A
5.解:过点C作CD⊥AB,垂足为D.
∵AB=4,BC=2,∴AC=2.
又∵S△ABC=AB·CD=BC·AC,
∴CD==.
(1)r=1.5 cm时,相离.
(2)r= cm时,相切.
(3)r=2 cm时,相交.
6.C
7.B
8.4.
9.解:过点O作OD⊥AB,垂足为D.
∵∠A=90°,∠C=60°,∴∠B=30°.
∴OD=OB=x.
当AB所在的直线与⊙O相切时,OD=r=2,
∴BO=4.
∴04时,相离.
10.相切或相交.
11.2__cm或8__cm.
12.B
13.D
14.相离.
15. 相交.
16.解:(1)∵⊙P的圆心在直线y=2x-1上,
∴圆心坐标可设为(x,2x-1).
当⊙P和x轴相切时,
2x-1=2或2x-1=-2,
解得x1=1.5,x2=-0.5.
∴P1(1.5,2),P2(-0.5,-2).
∵1.5<2,|-0.5|<2,
∴y轴与⊙P相交.
(2)当⊙P和y轴相切时,x=2或-2.
得2x-1=3或2x-1=-5.
∵|-5|>2,3>2,
∴x轴与⊙P相离.
(3)不能.∵当x=2时,y=3,
当x=-2时,y=-5,|-5|≠2,3≠2,
∴⊙P不能同时与x轴和y轴相切.
17.(1)1;
(2)1<d<3.
第2课时 切线的判定与性质
1.D
2.解:PD是⊙O的切线.
理由如下:
∵AB为直径,
∴∠ADB=90°.
∴∠ADO+∠ODB=90°.
∵OD=OB,
∴∠OBD=∠ODB.
∵∠PDA=∠PBD,
∴∠ADO+∠PDA=90°,即∠PDO=90°.
又∵直线PD经过⊙O半径的外端,
∴PD是⊙O的切线.
3.B
4.D
5.C
6.40°.
7.
解:连接OC.
∵AB与⊙O相切于点C,
∴OC⊥AB.
∵∠A=∠B,∴OA=OB.
∴AC=BC=AB=8.
∵OC=6,
∴OA==10.
8.(1,1)或(3,1)或(2,0)或(2,2).
9.C
10.A
11.30°.
12.
证明:连接OE,DE.
∵CD是⊙O的直径,
∴∠AED=∠CED=90°.
∵G是AD的中点,
∴EG=AD=DG.
∴∠GED=∠GDE.
∵OE=OD,
∴∠OED=∠ODE .
∴∠GED+∠OED=∠GDE+∠ODE,即∠OEG=∠ODG.
∵CD⊥AB,
∴∠ODG=90°.
∴∠OEG=90°.
又∵OE是⊙O的半径,
∴GE是⊙O的切线.
13.
解:(1)证明:连接OC.
∵OA=OB,CA=CB,
∴OC⊥AB.
∵OC是⊙O的半径,
∴AB是⊙O的切线.
(2)∵∠A=30°,∴OC=OA.
根据勾股定理,得OC2+AC2=OA2,
即(OA)2+AC2=OA2.
∵AC=6,∴OA=4.
∴OC=OA=2.
∴⊙O的周长为2π·2=4π.
14.
证明:连接OD.
∵DE为⊙O的切线,
∴OD⊥DE.
∴∠ODE=90°,
即∠2+∠ODC=90°.
∵OC=OD,
∴∠C=∠ODC.
∴∠2+∠C=90°.
而OC⊥OB,
∴∠C+∠3=90°.∴∠2=∠3.
∵∠1=∠3,∴∠1=∠2.
综合题
15.
解:(1)证明:连接CD.
∵BC为⊙O的直径,
∴∠BDC=90°.
∴CD⊥AB.
∵AC=BC,
∴∠ACD=∠BCD.
∵OC=OD,
∴∠BCD=∠ODC.
∴∠ODC=∠ACD.
∴OD∥AC.
∵DF⊥AC,
∴OD⊥EF.
又∵OD是⊙O的半径,
∴EF与⊙O相切.
(2)∵△ABC是等腰三角形,
∴BD=AD=6.
在Rt△BDC中,CD===8.
设AF=x,则CF=10-x.
在Rt△ADF和Rt△CDF中,
AD2-AF2=CD2-CF2.
∴62-x2=82-(10-x)2.
解得x=3.6.
∴DF==4.8.
第3课时 切线长定理
1.B
2.D
3.2.
4.4__cm.
5.解:设圆心为O,连接OA,OP.
3261995112395∵三角板有一个锐角为30°,
∴∠PAO=60°.
又∵PA与⊙O相切,
∴∠OPA=90°.∴∠POA=30°.
∵PA=5 cm,∴OP=5 cm.
∴铁环的半径为5 cm.
6.B
7.14__cm.
8.解:根据切线长定理,得
AE=AF,BF=BD,CE=CD.
设AF=AE=x cm,
则CE=CD=(28-x)cm,BF=BD=(18-x)cm.
∵BC=26 cm,
∴(18-x)+(28-x)=26.解得x=10.
∴AF=10 cm,BD=8 cm,CE=18 cm.
9.115°.
10.D
11.C
12.C
13.4.
14.解:∵点O为△ABC的外心,∠BOC=140°,
∴∠A=70°.
又∵点I为△ABC的内心,
∴∠BIC=90°+∠A=90°+35°=125°.
15.
证明:连接OA.
∵PA为⊙O的切线,
∴∠OAP=90°.
在Rt△AOP中,
∠AOP=90°-∠APO
=90°-30°=60°.
∴∠ACP=∠AOP=×60°=30°.
∴∠ACP=∠APO.∴AC=AP.
∴△ACP是等腰三角形.
第1课时 直线和圆的位置关系
1.已知半径为5的圆,其圆心到直线的距离是3,此时直线和圆的位置关系为( )
A.相离 B.相切 C.相交 D.无法确定
2.已知一条直线与圆有公共点,则这条直线与圆的位置关系是( )
A.相离 B.相切 C.相交 D.相切或相交
3.如图,∠O=30°,C为OB上一点,且OC=6,以点C为圆心,半径为3的圆与OA的位置关系是( )
A.相离 B.相交
C.相切 D.以上三种情况均有可能
4.⊙O的半径为6,一条弦长6,以3为半径的同心圆与这条弦的关系是( )
A.相切 B.相交
C.相离 D.相切或相交
5.在Rt△ABC中,∠C=90°,AB=4 cm,BC=2 cm,以C为圆心,r为半径的圆与AB有何种位置关系?请你写出判断过程.
(1)r=1.5 cm;(2)r= cm;(3)r=2 cm.
6.设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d的取值范围为( )
A.d≤4 B.d<4 C.d≥4 D.d=4
7.如图,在平面直角坐标系xOy中,半径为2的⊙P的圆心P的坐标为(-3,0),将⊙P沿x轴正方向平移,使⊙P与y轴相切,则平移的距离为( )
A.1 B.1或5 C.3 D.5
8.⊙O的半径为R,点O到直线l的距离为d,R,d是方程x2-4x+m=0的两根,当直线l与⊙O相切时,m的值为 .
9.如图,在Rt△ABC中,∠A=90°,∠C=60°,BO=x,⊙O的半径为2,当x在什么范围内取值时,AB所在的直线与⊙O相交、相切、相离?
10.已知⊙O的半径为2,直线l上有一点P满足PO=2,则直线l与⊙O的位置关系是
11.如图,⊙O的半径OC=5 cm,直线l⊥OC,垂足为H,且l交⊙O于A,B两点,AB=8 cm.若l沿OC所在直线平移与⊙O相切,则平移的距离是 .
12.如图,在Rt△ABC中,∠B=90°,∠A=60°,BC=4 cm,以B为圆心,2 cm长为半径作圆,则⊙B与AC的位置关系是( )
A.相离 B.相切 C.相交 D.外切
13.以坐标原点O为圆心,作半径为2的圆,若直线y=-x+b与⊙O相交,则b的取值范围是( )
A.0≤b<2 B.-2≤b≤2
C.-2
15. 如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于点N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上,则以MN为直径的圆与直线AB的位置关系是
16.如图所示,半径为2的⊙P的圆心在直线y=2x-1上运动.
(1)当⊙P和x轴相切时,写出点P的坐标;并判断此时y轴与⊙P的位置关系;
(2)当⊙P和y轴相切时,写出点P的坐标;并判断此时x轴与⊙P的位置关系;
(3)⊙P是否能同时与x轴和y轴相切?若能,写出点P的坐标;若不能,说明理由.
17.如图,给定一个半径长为2的圆,圆心O到水平直线l的距离为d,即OM=d.我们把圆上到直线l的距离等于1的点的个数记为m.如d=0时,l为经过圆心O的一条直线,此时圆上有四个到直线l的距离等于1的点,即m=4,由此可知:
(1)当d=3时,m= ;
(2)当m=2时,d的取值范围是 .
第2课时 切线的判定与性质
1.下列说法中,正确的是( )
A.AB垂直于⊙O的半径,则AB是⊙O的切线
B.经过半径外端的直线是圆的切线
C.经过切点的直线是圆的切线
D.圆心到直线的距离等于半径,那么这条直线是圆的切线
2.如图,AB是半圆的直径,O为圆心,AD,BD是半圆的弦,且∠PDA=∠PBD.判断直线PD是否为⊙O的切线,并说明理由.
3.如图,直线AB与⊙O相切于点A,⊙O的半径为2,若∠OBA=30°,则OB的长为( )
A.4 B.4 C.2 D.2
4.如图,已知直线AD是⊙O的切线,点A为切点,OD交⊙O于点B,点C在⊙O上,且∠ODA=36°,则∠ACB的度数为( )
A.54° B.36° C.30° D.27°
5.如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,PB=3,则⊙O的半径是( )
A.5 B.4 C.4.5 D.3.5
6.如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C等于 .
7.如图,AB与⊙O相切于点C,∠A=∠B,⊙O的半径为6,AB=16.求OA的长.
8.如图,在平面直角坐标系第一象限内有一矩形OABC,B(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心P的坐标为(1,1)或(3,1)或(2,0)或(2,2).
9.如图,两个同心圆的半径分别为4 cm和5 cm,大圆的一条弦AB与小圆相切,则弦AB的长为( )
A.3 cm B.4 cm C.6 cm D.8 cm
10.如图,AB为⊙O的直径,PD是⊙O的切线,点C为切点,PD与AB的延长线相交于点D,连接AC.若∠D=2∠CAD,CD=2,则BD的长为( )
A.2-2 B.2- C.2-1 D.-1
11.如图,以△AOB的顶点O为圆心,OA为半径的⊙O交BO于点C,此时AB恰好与⊙O相切,P为⊙O上任意一点(不与A,C重合),已知BC=AO,则∠P= .
12. 如图,已知CD是△ABC中AB边上的高,以CD为直径的⊙O分别交CA,CB于点E,F,点G是AD的中点.求证:GE是⊙O的切线.
13.如图,已知直线AB经过⊙O上的点C,且OA=OB,CA=CB.
(1)求证:直线AB是⊙O的切线;
(2)若∠A=30°,AC=6,求⊙O的周长.
14.如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,并与AB延长线交于点E.求证:∠1=∠2.
15.如图,等腰△ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
324612029210(1)求证:直线EF是⊙O的切线;
(2)求DF的值.
第3课时 切线长定理
1.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )
A.4 B.8 C.4 D.8
2.如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )
A.15° B.30° C.60° D.75°
3.如图,AB,AC,BD是⊙O的切线,P,C,D为切点,如果AB=5,AC=3,则BD的长为 .
4.如图,PA,PB是⊙O的切线,切点分别是A,B,若∠APB=60°,OA=2 cm,则OP= cm.
5.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径.若三角板与圆相切且测得PA=5 cm,求铁环的半径.
6.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
7.如图,△ABC中,AB=7 cm,AC=8 cm,BC=6 cm,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则△CEF的周长为 cm.
8.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC=26 cm,CA=28 cm,求AF,BD,CE的长.
9.如图,△ABC是圆的内接三角形,点P是△ABC的内心,∠A=50°,则∠BPC的度数为 .
10.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( )
A.9 B.10 C.12 D.14
11.如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6 m和8 m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是( )
A.2 m B.3 m C.6 m D.9 m
12.如图,菱形ABCD的边长为10,⊙O分别与AB,AD相切于E,F两点,且与BG相切于点G.若AO=5,且⊙O的半径为3,则BG的长度为( )
A.4 B.5 C.6 D.7
13.如图,PA,PB分别与⊙O相切于点A,B,⊙O的切线EF分别交PA,PB于点E,F,切点C在上,若PA长为2,则△PEF的周长为 .
14.如图所示,点I为△ABC的内心,点O为△ABC的外心,若∠BOC=140°,求∠BIC的度数.
15.如图,CD是⊙O的直径,且CD=2 cm,点P为CD的延长线上一点,过点P作⊙O的切线PA,PB,切点分别为点A,B.
(1)连接AC,若∠APO=30°,试证明△ACP是等腰三角形;
(2)填空:
①当DP=1cm时,四边形AOBD是菱形;
②当DP=(-1)cm时,四边形AOBP是正方形.
参考答案:
24.2.2 直线和圆的位置关系
第1课时 直线和圆的位置关系
1.C
2.D
3.C
4.A
5.解:过点C作CD⊥AB,垂足为D.
∵AB=4,BC=2,∴AC=2.
又∵S△ABC=AB·CD=BC·AC,
∴CD==.
(1)r=1.5 cm时,相离.
(2)r= cm时,相切.
(3)r=2 cm时,相交.
6.C
7.B
8.4.
9.解:过点O作OD⊥AB,垂足为D.
∵∠A=90°,∠C=60°,∴∠B=30°.
∴OD=OB=x.
当AB所在的直线与⊙O相切时,OD=r=2,
∴BO=4.
∴0
10.相切或相交.
11.2__cm或8__cm.
12.B
13.D
14.相离.
15. 相交.
16.解:(1)∵⊙P的圆心在直线y=2x-1上,
∴圆心坐标可设为(x,2x-1).
当⊙P和x轴相切时,
2x-1=2或2x-1=-2,
解得x1=1.5,x2=-0.5.
∴P1(1.5,2),P2(-0.5,-2).
∵1.5<2,|-0.5|<2,
∴y轴与⊙P相交.
(2)当⊙P和y轴相切时,x=2或-2.
得2x-1=3或2x-1=-5.
∵|-5|>2,3>2,
∴x轴与⊙P相离.
(3)不能.∵当x=2时,y=3,
当x=-2时,y=-5,|-5|≠2,3≠2,
∴⊙P不能同时与x轴和y轴相切.
17.(1)1;
(2)1<d<3.
第2课时 切线的判定与性质
1.D
2.解:PD是⊙O的切线.
理由如下:
∵AB为直径,
∴∠ADB=90°.
∴∠ADO+∠ODB=90°.
∵OD=OB,
∴∠OBD=∠ODB.
∵∠PDA=∠PBD,
∴∠ADO+∠PDA=90°,即∠PDO=90°.
又∵直线PD经过⊙O半径的外端,
∴PD是⊙O的切线.
3.B
4.D
5.C
6.40°.
7.
解:连接OC.
∵AB与⊙O相切于点C,
∴OC⊥AB.
∵∠A=∠B,∴OA=OB.
∴AC=BC=AB=8.
∵OC=6,
∴OA==10.
8.(1,1)或(3,1)或(2,0)或(2,2).
9.C
10.A
11.30°.
12.
证明:连接OE,DE.
∵CD是⊙O的直径,
∴∠AED=∠CED=90°.
∵G是AD的中点,
∴EG=AD=DG.
∴∠GED=∠GDE.
∵OE=OD,
∴∠OED=∠ODE .
∴∠GED+∠OED=∠GDE+∠ODE,即∠OEG=∠ODG.
∵CD⊥AB,
∴∠ODG=90°.
∴∠OEG=90°.
又∵OE是⊙O的半径,
∴GE是⊙O的切线.
13.
解:(1)证明:连接OC.
∵OA=OB,CA=CB,
∴OC⊥AB.
∵OC是⊙O的半径,
∴AB是⊙O的切线.
(2)∵∠A=30°,∴OC=OA.
根据勾股定理,得OC2+AC2=OA2,
即(OA)2+AC2=OA2.
∵AC=6,∴OA=4.
∴OC=OA=2.
∴⊙O的周长为2π·2=4π.
14.
证明:连接OD.
∵DE为⊙O的切线,
∴OD⊥DE.
∴∠ODE=90°,
即∠2+∠ODC=90°.
∵OC=OD,
∴∠C=∠ODC.
∴∠2+∠C=90°.
而OC⊥OB,
∴∠C+∠3=90°.∴∠2=∠3.
∵∠1=∠3,∴∠1=∠2.
综合题
15.
解:(1)证明:连接CD.
∵BC为⊙O的直径,
∴∠BDC=90°.
∴CD⊥AB.
∵AC=BC,
∴∠ACD=∠BCD.
∵OC=OD,
∴∠BCD=∠ODC.
∴∠ODC=∠ACD.
∴OD∥AC.
∵DF⊥AC,
∴OD⊥EF.
又∵OD是⊙O的半径,
∴EF与⊙O相切.
(2)∵△ABC是等腰三角形,
∴BD=AD=6.
在Rt△BDC中,CD===8.
设AF=x,则CF=10-x.
在Rt△ADF和Rt△CDF中,
AD2-AF2=CD2-CF2.
∴62-x2=82-(10-x)2.
解得x=3.6.
∴DF==4.8.
第3课时 切线长定理
1.B
2.D
3.2.
4.4__cm.
5.解:设圆心为O,连接OA,OP.
3261995112395∵三角板有一个锐角为30°,
∴∠PAO=60°.
又∵PA与⊙O相切,
∴∠OPA=90°.∴∠POA=30°.
∵PA=5 cm,∴OP=5 cm.
∴铁环的半径为5 cm.
6.B
7.14__cm.
8.解:根据切线长定理,得
AE=AF,BF=BD,CE=CD.
设AF=AE=x cm,
则CE=CD=(28-x)cm,BF=BD=(18-x)cm.
∵BC=26 cm,
∴(18-x)+(28-x)=26.解得x=10.
∴AF=10 cm,BD=8 cm,CE=18 cm.
9.115°.
10.D
11.C
12.C
13.4.
14.解:∵点O为△ABC的外心,∠BOC=140°,
∴∠A=70°.
又∵点I为△ABC的内心,
∴∠BIC=90°+∠A=90°+35°=125°.
15.
证明:连接OA.
∵PA为⊙O的切线,
∴∠OAP=90°.
在Rt△AOP中,
∠AOP=90°-∠APO
=90°-30°=60°.
∴∠ACP=∠AOP=×60°=30°.
∴∠ACP=∠APO.∴AC=AP.
∴△ACP是等腰三角形.
同课章节目录
