函数的单调性

(共25张PPT)
函数的单调性
济源市第六中学 范小魁
分别作出下列函数的图像：
（1）　　　 （2）　 　（3）
根据三个函数图像，分别指出当x∈(－∞，＋∞)时，图像的变化趋势？
一：问题情境
x
y
y=2x
O
1
1
2
-1
2
-1
-2
-2
y
y= -2x
O
1
1
2
-1
2
-1
-2
-2
x
x
y
y=x2
O
1
1
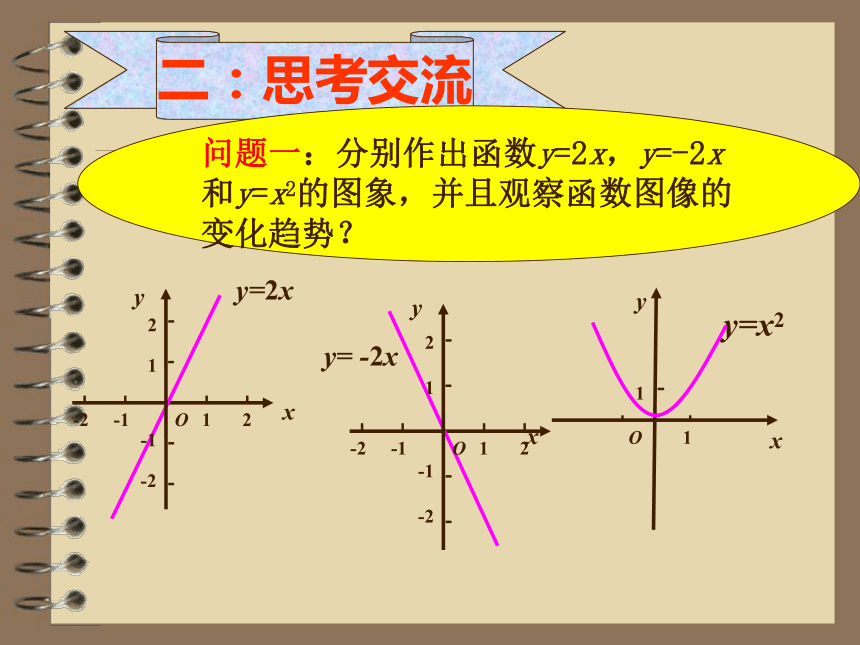
二：思考交流
问题一：分别作出函数y=2x，y=-2x和y=x2的图象，并且观察函数图像的变化趋势？
在某一区间内，
图象在该区间呈上升趋势
当x的值增大时，函数值y也增大，此时函数是
增加的
图象在该区间呈下降趋势，
当x的值增大时，函数值y反而减小，此时函数 是减少的
函数的这种性质称为函数的单调性。
问题二：你能明确地说出“图象呈逐渐上升趋势”的意思吗？
y=x2在（－∞，０）上是减少的，
在（０，＋∞）上是增加的。
问题三：请说出y=x2 在什么时候是增加的，什么时候是减少的？
x
y
y=x2
O
1
1
如果函数在某个区间上随自变量x的增大，y也越来越大，我们说函数在该区间上是增加的；
如果函数在某个区间上随自变量x的增大，y越来越小，我们说函数在该区间上是减少的．
问题四：能否用自己的理解说说什么是增函数，什么是减函数？
x
y
y=x2
O
1
1
问题五：如何从解析式的角度说明y=x2在 上是增加的？
问题五：如何从解析式的角度说明y=x2在 上是增加的？
1.增（减）函数的定义
设函数f（x）的定义域为I：
（1）如果对于定义域I内某个区间D上的任意两个自变量的值x1 ， x2 ，当x1 ＜ x2时，都有f（ x1 ）＜f（ x2 ），那么我们就说函数f（x）在区间Ｄ上是增加的（如下图1）
三：抽象概括
（2） 如果对于定义域I内某个区间D上的任意两个自变量的值x1 ， x2 ，当x1 ＜ x2时，都有f（ x1 ）＞f（ x2 ），那么我们就说函数f（x）在区间Ｄ上是 减少的（如下图2）
课时小结
2 .单调区间的概念
如果函数y＝f（x）在区间D上是增加的或是减少的，那么我们就说函数y＝f（x）在这一区间具有（严格的）单调性，区间D叫作y＝f（x）的单调区间．
如果函数y＝f（x）在整个定义域内是增加的或减少的，我们称这个函数是增函数（或减函数），统称为单调函数。
小结
判断题：
①若函数f(x)满足f(2) ＜f(3)则函数f(x)在区间[2,3]上是增加的.
② 因为函数f(x)在区间(-∞,0)和[0,+∞)上都是递增的 ，所以在(-∞,0) ∪[0,+∞)上也是递增的.
四、深化定义
y
x
O
2
3
f(2)
f(3)
①若函数f(x)满足f(2) ＜f(3)则函数f(x)在区间[2,3]上是增加的．
② 因为函数f(x)在区间(-∞,0)和[0,+∞)上都是递增 ，所以在(-∞,0) ∪[0,+∞)上也是递增的.
o
x
y
O
o
x
y
O
注意：
①单调性是对定义域的某个区间上的整体性质，自变量具有任意性，不能用特殊值说明问题。
②函数在定义域内的两个区间A,B上都是增加的（或减少的），函数在 上不一定是增加的（或减少的）．
2 4 6 8 10 12 14 16 18 20 22 24
10
8
6
4
2
-2
0
θ/ C
t/h
y＝f(x)，x∈[0，24]
例1、根据图象说出函数的单调区间
[0，4]
[4，14]
[14，24]
五、例题分析
例2、画出下列函数图象，并写出单调区间：
y
x
O
2
1
2
1
-1
-2
两区间之间用和或用逗号隔开.
能否写成
y
x
O
x1
x2
例3、证明：函数f（x）＝2x＋1，在(－∞，＋∞）上是增函数．
思考：如何证明函数的单调性？怎样判断f(x1)与f(x2)的大小？
例3：证明函数f(x)=3x+2在R上是增函数。
f(x1)-f(x2)=(3 x1 +2)-(3 x2+2)
由x1即 f(x1)证明：设x1,x2是R上的任意两个实数，且x1=3( x1- x2)
于是 f(x1)-f(x2)<0
所以，函数f(x)=3x+2在R上是增函数。
取值
定号
变形
作差
判断
end
返回
1. 证明函数单调性的步骤：
（1）设量
（2）作差
（3）变形（到能够判号为止）
（4）定号 （差的符号是大于零还是小于零）
（5）判断
2.求函数单调区间的方法可以利用函数图像数形结合
方法总结
1, 证明函数f（x）＝x2－x在（－∞，］上是减少的．
六：课堂练习
∴函数f（x）＝x2－x在（－∞，］上是减少的．
证明:设
七：课时小结
1.增（减）函数的定义
2.单调函数 、单调区间的定义
3.用定义证明函数单调性的步骤
4.求简单函数单调区间的方法
谢谢！