1.5.1.2 含乘方的有理数混合运算 课件(共20张PPT)
文档属性
| 名称 | 1.5.1.2 含乘方的有理数混合运算 课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 00:00:00 | ||
图片预览








文档简介
1.5.1
有理数的乘方
第一章
有理数
第二课时
含乘方的有理数混合运算
人教版
七上
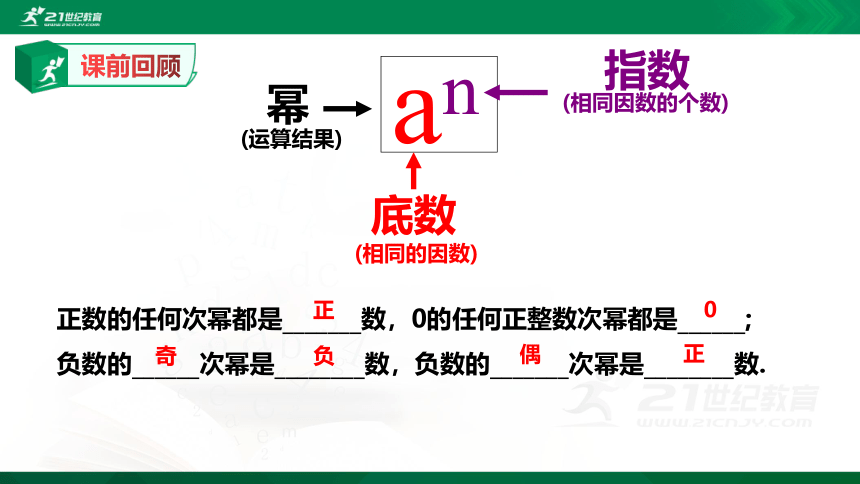
an
幂
底数
指数
(运算结果)
(相同的因数)
(相同因数的个数)
正数的任何次幂都是_______数,0的任何正整数次幂都是______;
负数的______次幂是________数,负数的_______次幂是________数.
正
0
奇
负
偶
正
课前回顾
1、能按照有理数的运算顺序,正确熟练进行有理数加、减、乘、除、乘方的混合运算;
2、培养学生观察能力和运算能力;
3、培养学生在计算前认真审题,确定运算顺序,计算中按审慎进行,最后检查的好习惯。
重点
正确进行有理数混合运算。
难点
掌握有理数的运算顺序。
学习目标
加减运算
乘方运算
第一级运算
第三级运算
乘除运算
第二级运算
有理数的混合运算
想一想:
有理数混合运算应按怎样的运算顺序进行计算呢?
复习导入
有理数混合运算顺序
1、先乘方,再乘除,最后加减;
2、同级运算,从左到右进行;
3、如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
归纳小结
计算:
=1×2
+(-8)÷4
=2-2
=0
=-125-3×????????????
=
-?????????????????????????
?
针对练习
例1:计算
解:
典例分析
例1:计算
解:
C
针对练习
2.计算:
(2)(-4)×(-
)÷(-
)-(-
)3.
(1)-14-
×[2-(-4)2].
=-1-
×(2-16)
=-1-
×(-14)
=-1+
=
解:原式
解:原式
=(-4)×(-
)×(-
)-(-
)
=-5+
=-4
针对练习
观察下列三行数:
-2,
4,-8,
16,-32,
64,…;
①
0,
6,-6,
18,-30,
66,…;
②
-1,
2,-4,
8,-16,
32,….
③
(1)第①行数按什么规律排列?
【提示】观察①,各数均为2的倍数,联系乘方,从符号及绝对值两个方面考虑,可以发现排列的规律。
解:
例2
典例分析
观察下列三行数:
-2,
4,-8,
16,-32,
64,…;
①
0,
6,-6,
18,-30,
66,…;
②
-1,
2,-4,
8,-16,
32,….
③
(2)第②③行数与第①行数分别有什么关系?
解:(2)对比①②两行中位置对应的数,可以发现:
第②行数是第①行相应的数加2,即
第③行数是第①行相应的数乘0.5,即
-2×0.5,(?2)2×0.5,(?2)3×0.5,
(?2)4×0.5,…
?
观察下列三行数:
-2,
4,-8,
16,-32,
64,…;
①
0,
6,-6,
18,-30,
66,…;
②
-1,
2,-4,
8,-16,
32,….
③
(3)取每行数的第10个数,计算这三个数的和?
1.根据规律填空;
(1)1,4,9,16,25,36,______,______,...
(2)0,3,8,15,24,_______,_______,...
2.观察下列按规律排列的等式:0+1=12,2×1+2=22,3×2+3=32,4×3+4=42,...
请猜想第10个等式应为____________________,
请猜想第n个等式应为___________________。
49
64
35
48
10×9+10=102
n×(n-1)+n=n2
针对练习
1.计算-2×32-(-2×3)2等于( )
A.
0 B.
-54
C.
-72
D.
-18
B
课堂练习
2.计算:
答案:(1)1
(2)21
(3)-9
(4)-8
3.已知m=b1+b2+b3+b4+···+b1000,
当b=-1时,求m5的值.
当b=-1时,
m=b1+b2+b3+b4+···+b1000
=(-1)
1+
(-1)
2+
(-1)
3
+
(-1)4
+
···+
(-1)1000=-1+1-1+1
-
···-1+1
=0.
所以m5=05=0.
4.
将一底面半径是10cm,高为30cm的圆柱形水桶中装满了水,小明先将桶中的水倒满2个底面半径为3cm,高为6cm的圆柱形杯子,再把剩下的水倒入长、宽、高分别为50cm,30cm和20cm的长方体容器内,长方体容器内水的高度大约是多少厘米?(π取3,容器的厚度忽略不计,计算结果取整数)
解:(3×102×30-3×32×6×2)÷(50×30)=(9000-324)÷1500≈6cm.
1.乘方与加、减、乘、除的混合运算,
运算顺序是:先乘方,再乘除,最后加减;
2.数字规律探究.
课堂小结
有理数的乘方
第一章
有理数
第二课时
含乘方的有理数混合运算
人教版
七上
an
幂
底数
指数
(运算结果)
(相同的因数)
(相同因数的个数)
正数的任何次幂都是_______数,0的任何正整数次幂都是______;
负数的______次幂是________数,负数的_______次幂是________数.
正
0
奇
负
偶
正
课前回顾
1、能按照有理数的运算顺序,正确熟练进行有理数加、减、乘、除、乘方的混合运算;
2、培养学生观察能力和运算能力;
3、培养学生在计算前认真审题,确定运算顺序,计算中按审慎进行,最后检查的好习惯。
重点
正确进行有理数混合运算。
难点
掌握有理数的运算顺序。
学习目标
加减运算
乘方运算
第一级运算
第三级运算
乘除运算
第二级运算
有理数的混合运算
想一想:
有理数混合运算应按怎样的运算顺序进行计算呢?
复习导入
有理数混合运算顺序
1、先乘方,再乘除,最后加减;
2、同级运算,从左到右进行;
3、如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行。
归纳小结
计算:
=1×2
+(-8)÷4
=2-2
=0
=-125-3×????????????
=
-?????????????????????????
?
针对练习
例1:计算
解:
典例分析
例1:计算
解:
C
针对练习
2.计算:
(2)(-4)×(-
)÷(-
)-(-
)3.
(1)-14-
×[2-(-4)2].
=-1-
×(2-16)
=-1-
×(-14)
=-1+
=
解:原式
解:原式
=(-4)×(-
)×(-
)-(-
)
=-5+
=-4
针对练习
观察下列三行数:
-2,
4,-8,
16,-32,
64,…;
①
0,
6,-6,
18,-30,
66,…;
②
-1,
2,-4,
8,-16,
32,….
③
(1)第①行数按什么规律排列?
【提示】观察①,各数均为2的倍数,联系乘方,从符号及绝对值两个方面考虑,可以发现排列的规律。
解:
例2
典例分析
观察下列三行数:
-2,
4,-8,
16,-32,
64,…;
①
0,
6,-6,
18,-30,
66,…;
②
-1,
2,-4,
8,-16,
32,….
③
(2)第②③行数与第①行数分别有什么关系?
解:(2)对比①②两行中位置对应的数,可以发现:
第②行数是第①行相应的数加2,即
第③行数是第①行相应的数乘0.5,即
-2×0.5,(?2)2×0.5,(?2)3×0.5,
(?2)4×0.5,…
?
观察下列三行数:
-2,
4,-8,
16,-32,
64,…;
①
0,
6,-6,
18,-30,
66,…;
②
-1,
2,-4,
8,-16,
32,….
③
(3)取每行数的第10个数,计算这三个数的和?
1.根据规律填空;
(1)1,4,9,16,25,36,______,______,...
(2)0,3,8,15,24,_______,_______,...
2.观察下列按规律排列的等式:0+1=12,2×1+2=22,3×2+3=32,4×3+4=42,...
请猜想第10个等式应为____________________,
请猜想第n个等式应为___________________。
49
64
35
48
10×9+10=102
n×(n-1)+n=n2
针对练习
1.计算-2×32-(-2×3)2等于( )
A.
0 B.
-54
C.
-72
D.
-18
B
课堂练习
2.计算:
答案:(1)1
(2)21
(3)-9
(4)-8
3.已知m=b1+b2+b3+b4+···+b1000,
当b=-1时,求m5的值.
当b=-1时,
m=b1+b2+b3+b4+···+b1000
=(-1)
1+
(-1)
2+
(-1)
3
+
(-1)4
+
···+
(-1)1000=-1+1-1+1
-
···-1+1
=0.
所以m5=05=0.
4.
将一底面半径是10cm,高为30cm的圆柱形水桶中装满了水,小明先将桶中的水倒满2个底面半径为3cm,高为6cm的圆柱形杯子,再把剩下的水倒入长、宽、高分别为50cm,30cm和20cm的长方体容器内,长方体容器内水的高度大约是多少厘米?(π取3,容器的厚度忽略不计,计算结果取整数)
解:(3×102×30-3×32×6×2)÷(50×30)=(9000-324)÷1500≈6cm.
1.乘方与加、减、乘、除的混合运算,
运算顺序是:先乘方,再乘除,最后加减;
2.数字规律探究.
课堂小结
