华东师大版九年级上册数学教案 23.3.3 相似三角形的性质(表格式)
文档属性
| 名称 | 华东师大版九年级上册数学教案 23.3.3 相似三角形的性质(表格式) |
|
|
| 格式 | zip | ||
| 文件大小 | 142.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览


文档简介
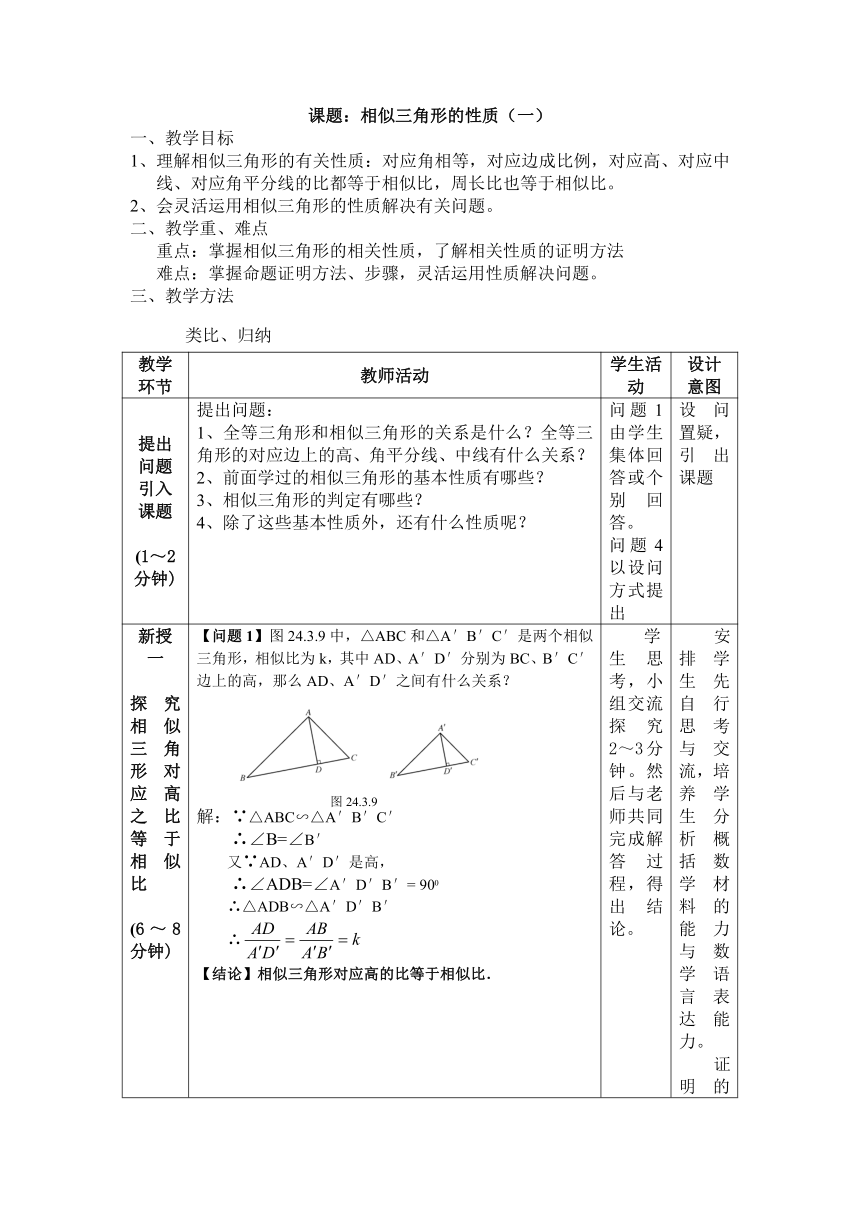
课题:相似三角形的性质(一)
一、教学目标
理解相似三角形的有关性质:对应角相等,对应边成比例,对应高、对应中线、对应角平分线的比都等于相似比,周长比也等于相似比。
会灵活运用相似三角形的性质解决有关问题。
二、教学重、难点
重点:掌握相似三角形的相关性质,了解相关性质的证明方法
难点:掌握命题证明方法、步骤,灵活运用性质解决问题。
三、教学方法
类比、归纳
教学环节
教师活动
学生活动
设计意图
提出问题
引入课题
(1~2分钟)
提出问题:
1、全等三角形和相似三角形的关系是什么?全等三角形的对应边上的高、角平分线、中线有什么关系?
2、前面学过的相似三角形的基本性质有哪些?
3、相似三角形的判定有哪些?
4、除了这些基本性质外,还有什么性质呢?
问题1由学生集体回答或个别回答。
问题4以设问方式提出
设问置疑,
引出课题
新授一
探究相似三角形对应高之比等于相似比
(6~8分钟)
【问题1】图24.3.9中,△ABC和△A′B′C′是两个相似三角形,相似比为k,其中AD、A′D′分别为BC、B′C′边上的高,那么AD、A′D′之间有什么关系?
解:∵△ABC∽△A′B′C′
∴∠B=∠B′
又∵AD、A′D′是高,
∴∠ADB=∠A′D′B′=
900
∴△ADB∽△A′D′B′
∴
【结论】相似三角形对应高的比等于相似比.
学生思考,小组交流探究2~3分钟。然后与老师共同完成解答过程,得出结论。
安排学生先自行思考与交流,培养学生分析概括数学材料的能力与数学语言表达能力。
证明的过程通过老师书写出来,培养学生规范书写证明过程的习惯。
思考探索归纳其它性质
(3~5分钟)
自主思考---类似结论
【问题2】,.△ABC∽△A′B′C′,相似比为k,其中AE、
A′E′
分别为BC、
B′
C′边上的中线,那么?
结论:相似三角形对应中线的比等于相似比.
△ABC∽△A′B′C′,相似比为k,其中AE、
A′E′
分别为BC、
B′C′边上的角平分线,那么?
结论:相似三角形对应角的角平分线的比等于相似比.
【思考】
相似三角形的对应角平分线之比等于什么?
相似三角形的对应中线之比等于什么?
相似三角形的周长之比等于什么?
(说明:详细证明过程留待学生课后通过作业形式完成)
思考题学生口头回答、听教师简单分析,或个别提问学生。
归纳总结,简单分析,注意把握时间。
应用举例
(8~10分钟)
例1:已知△ABC∽
△A?B
?C
?,BD和B
?D
?分别是△ABC和△A?B?C?中线,且AB=10,A?B?=2,BD=6。求B?D?的长。
解略(见课件)
学生先思考,然后上黑板板书过程,师生共同检查订正。
这是性质的直接应用,注意学生的规范书写解题过程。
应用练习
(2~3分钟)
练习一:随堂练习见课件
练习二:《直击新课标》42页第1~4题
学生思考并口头回答。
题型主要以填空、选择为主,不必加深难度。
知识小结
(约2分钟)
提问学生:相似三角形的性质有哪些?
相似三角形的对应边成比例,对应角相等。
相似三角形的对应高之比,对应角平分线之比、对应中线之比、周长之比等于相似比。
相似三角形的面积比等于相似比的平方。
师生共同小结,使知识系统化。
利用提问式小结,引导学生梳理知识。
分层作业
1、完成《直击新课标》42~43页其余题,
2、预习课本第相似三角形周长和面积的比等于什么?
3、学生可适当自主选做《随堂优化训练》第35页1~6题。
【板书设计】
黑板一:板书课题与几个性质。
黑板二:两个性质的证明过程。
黑板三:应用举例,学生板演与老师点评分析。
黑板四:练习的分析与其它。
一、教学目标
理解相似三角形的有关性质:对应角相等,对应边成比例,对应高、对应中线、对应角平分线的比都等于相似比,周长比也等于相似比。
会灵活运用相似三角形的性质解决有关问题。
二、教学重、难点
重点:掌握相似三角形的相关性质,了解相关性质的证明方法
难点:掌握命题证明方法、步骤,灵活运用性质解决问题。
三、教学方法
类比、归纳
教学环节
教师活动
学生活动
设计意图
提出问题
引入课题
(1~2分钟)
提出问题:
1、全等三角形和相似三角形的关系是什么?全等三角形的对应边上的高、角平分线、中线有什么关系?
2、前面学过的相似三角形的基本性质有哪些?
3、相似三角形的判定有哪些?
4、除了这些基本性质外,还有什么性质呢?
问题1由学生集体回答或个别回答。
问题4以设问方式提出
设问置疑,
引出课题
新授一
探究相似三角形对应高之比等于相似比
(6~8分钟)
【问题1】图24.3.9中,△ABC和△A′B′C′是两个相似三角形,相似比为k,其中AD、A′D′分别为BC、B′C′边上的高,那么AD、A′D′之间有什么关系?
解:∵△ABC∽△A′B′C′
∴∠B=∠B′
又∵AD、A′D′是高,
∴∠ADB=∠A′D′B′=
900
∴△ADB∽△A′D′B′
∴
【结论】相似三角形对应高的比等于相似比.
学生思考,小组交流探究2~3分钟。然后与老师共同完成解答过程,得出结论。
安排学生先自行思考与交流,培养学生分析概括数学材料的能力与数学语言表达能力。
证明的过程通过老师书写出来,培养学生规范书写证明过程的习惯。
思考探索归纳其它性质
(3~5分钟)
自主思考---类似结论
【问题2】,.△ABC∽△A′B′C′,相似比为k,其中AE、
A′E′
分别为BC、
B′
C′边上的中线,那么?
结论:相似三角形对应中线的比等于相似比.
△ABC∽△A′B′C′,相似比为k,其中AE、
A′E′
分别为BC、
B′C′边上的角平分线,那么?
结论:相似三角形对应角的角平分线的比等于相似比.
【思考】
相似三角形的对应角平分线之比等于什么?
相似三角形的对应中线之比等于什么?
相似三角形的周长之比等于什么?
(说明:详细证明过程留待学生课后通过作业形式完成)
思考题学生口头回答、听教师简单分析,或个别提问学生。
归纳总结,简单分析,注意把握时间。
应用举例
(8~10分钟)
例1:已知△ABC∽
△A?B
?C
?,BD和B
?D
?分别是△ABC和△A?B?C?中线,且AB=10,A?B?=2,BD=6。求B?D?的长。
解略(见课件)
学生先思考,然后上黑板板书过程,师生共同检查订正。
这是性质的直接应用,注意学生的规范书写解题过程。
应用练习
(2~3分钟)
练习一:随堂练习见课件
练习二:《直击新课标》42页第1~4题
学生思考并口头回答。
题型主要以填空、选择为主,不必加深难度。
知识小结
(约2分钟)
提问学生:相似三角形的性质有哪些?
相似三角形的对应边成比例,对应角相等。
相似三角形的对应高之比,对应角平分线之比、对应中线之比、周长之比等于相似比。
相似三角形的面积比等于相似比的平方。
师生共同小结,使知识系统化。
利用提问式小结,引导学生梳理知识。
分层作业
1、完成《直击新课标》42~43页其余题,
2、预习课本第相似三角形周长和面积的比等于什么?
3、学生可适当自主选做《随堂优化训练》第35页1~6题。
【板书设计】
黑板一:板书课题与几个性质。
黑板二:两个性质的证明过程。
黑板三:应用举例,学生板演与老师点评分析。
黑板四:练习的分析与其它。
