人教版九年级数学上册 24.4 弧长和扇形面积 同步测试题(Word版有答案)
文档属性
| 名称 | 人教版九年级数学上册 24.4 弧长和扇形面积 同步测试题(Word版有答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 112.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览



文档简介
24.4
弧长和扇形面积
同步测试题
(满分120分;时间:120分钟)
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
如图,当半径为的转轮转过角时,传送带上的物体平移的距离为
.
A.
B.
C.
D.
?
2.
如果圆锥的底面半径为,母线长为,那么它的侧面积等于?
?
?
?
A.
B.
C.
D.
?
3.
如图,已知:是的内接三角形,,若,则图中阴影部分的面积是(
)
A.
B.
C.
D.
?
4.
、两条弧长相等,弧所对的圆心角是弧所对圆心角的一半,则弧所在圆的半径与弧所圆的半径之间的关系是(
)
A.
B.
C.
D.无法确定
?
5.
如图,是一个圆锥形冰激凌,已知它的母线长是,高是,则这个圆锥形冰激凌的底面面积是(
)
A.
B.
C.
D.
?
6.
如图,以为直径,点为圆心的半圆经过点,若,则图中阴影部分的面积是(?
?
?
?
)
A.
B.
C.
D.
?
7.
在半径为的圆中,的圆心角所对的弧长是(
)
A.
B.
C.
D.
?
8.
若圆锥的侧面展开图的弧长为,则此圆锥底面的半径为
.
A.
B.
C.
D.
?
9.
一个圆锥的底面周长是,高,沿直径把它切成相等的两半,表面积增加了?
?
?
??.(取)
A.
B.
C.
D.
?
10.
用一张面积为的正方形硬纸片围成一个圆柱的侧面,则这个圆柱的底面直径为(
)(不计接缝,精确到)
A.
B.
C.
D.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
,
)
?
11.
如果圆柱的母线长为,底面半径为,那么这个圆柱的侧面积是________.
?
12.
已知扇形的圆心角为,面积为,则扇形弧长为________.
?
13.
在半径为的圆中,的圆心角所对的弧长等于________.
?
14.
半径为,圆心角为的扇形的面积为________.
?
15.
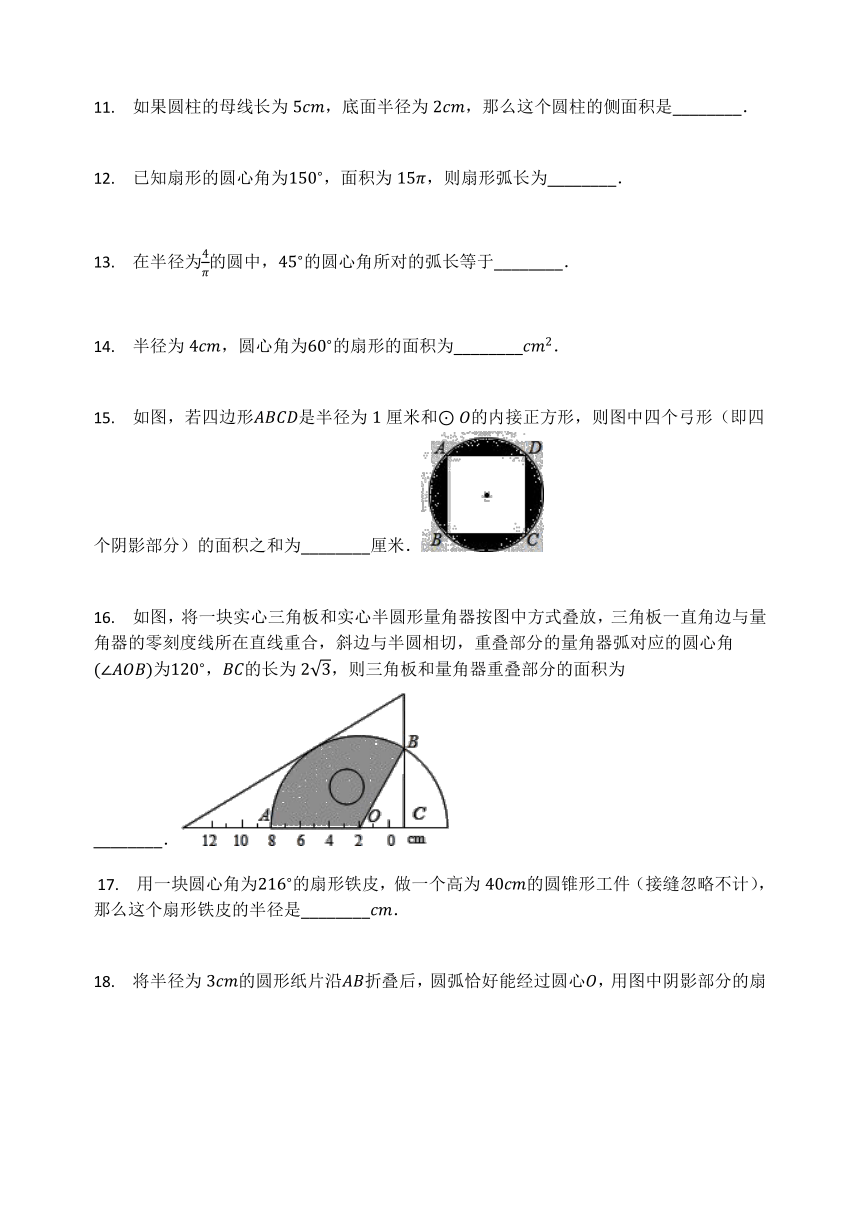
如图,若四边形是半径为厘米和的内接正方形,则图中四个弓形(即四个阴影部分)的面积之和为________厘米.
?
16.
如图,将一块实心三角板和实心半圆形量角器按图中方式叠放,三角板一直角边与量角器的零刻度线所在直线重合,斜边与半圆相切,重叠部分的量角器弧对应的圆心角为,的长为,则三角板和量角器重叠部分的面积为________.
?17.
用一块圆心角为的扇形铁皮,做一个高为的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是________.
?
18.
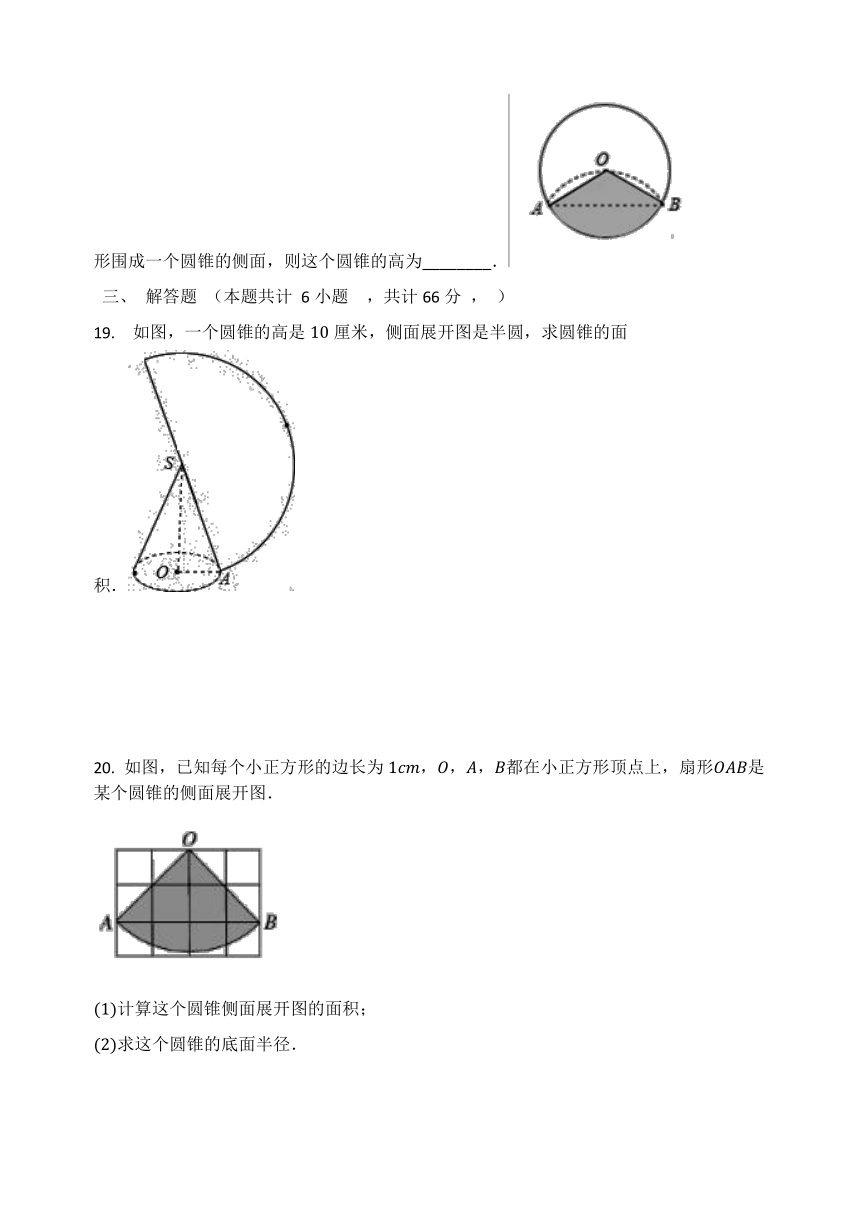
将半径为的圆形纸片沿折叠后,圆弧恰好能经过圆心,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为________.
三、
解答题
(本题共计
6小题
,共计66分
,
)
?
19.
如图,一个圆锥的高是厘米,侧面展开图是半圆,求圆锥的面积.
?
20.
如图,已知每个小正方形的边长为,,,都在小正方形顶点上,扇形是某个圆锥的侧面展开图.
计算这个圆锥侧面展开图的面积;
求这个圆锥的底面半径.
?
21.
某商店要制作圣诞节的圆锥形纸帽,已知纸帽的底面周长为,高为,要制作个这样的帽子要用多少平方厘米的纸?
?
22.
如图,,,以为直径画半圆交于,如果图中①的面积为,求阴影部分的面积.
?
23.
如图,圆锥的底面半径为,高为,求这个圆锥的侧面积和表面积.
?
?24.
如图是某学校田径体育场一部分的示意图,第一条跑道每圈为米,跑道分直道和弯道,直道为长相等的平行线段,弯道为同心的半圆型,弯道与直道相连接,已知直道的长米,跑道的宽为米.,结果精确到
(1)求第一条跑道的弯道部分的半径.
(2)求一圈中第二条跑道比第一条跑道长多少米?
(3)若进行米比赛,求第六道的起点与圆心的连线与的夹角的度数.
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
2.
【答案】
B
3.
【答案】
B
4.
【答案】
C
5.
【答案】
B
6.
【答案】
A
7.
【答案】
A
8.
【答案】
C
9.
【答案】
C
10.
【答案】
C
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
12.
【答案】
13.
【答案】
14.
【答案】
15.
【答案】
16.
【答案】
17.
【答案】
18.
【答案】
、
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
解:设圆锥底面圆的半径为,母线长为,
,所以,
在中,
∵
,
∴
,,
∴
,
∴
圆锥的面积.
20.
【答案】
解:由图可知,,
则弧的长为,
∴
面积为:.
设底面半径为,
则,
.
答:这个圆锥的底面半径为.
21.
【答案】
解:∵
纸帽的底面周长为,
∴
底面半径为:,
∴
母线长为:,
∴
一个圆锥形纸帽侧面积为:,
∴
要制作个这样的帽子要用平方厘米的纸.
22.
【答案】
解:设,
∵
,
∴
,
∵
,
∴
,
,
∴
图中①的面积.
23.
【答案】
解:∵
圆锥的底面半径为,高为,
∴
圆锥的母线长为,
∴
.
∵
圆锥的底面积,
∴
.
24.
【答案】
这个圆锥漏斗的侧面积是.
侧面展开图所对的圆心角是.
25.
【答案】
解:(1)弯道的半圆周长为(米),
由圆周长,所以半圆弧长
则第一道弯道部分的半径
(2)第二道与第一道的直跑道长相等,第二道与第一道的弯跑道的半径之差为米,第二道与第一道的弯跑道长的差即为两圆周长之差,即(米).
(3)从第一跑道米,是以点为始点,第六跑道上的运动员需要跑米的直道和米的弯道,即弧长为米,又第六道弯道半圆的半径为米,
由弧长与半圆,圆心角的关系得:,
所以.
弧长和扇形面积
同步测试题
(满分120分;时间:120分钟)
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
,
)
?1.
如图,当半径为的转轮转过角时,传送带上的物体平移的距离为
.
A.
B.
C.
D.
?
2.
如果圆锥的底面半径为,母线长为,那么它的侧面积等于?
?
?
?
A.
B.
C.
D.
?
3.
如图,已知:是的内接三角形,,若,则图中阴影部分的面积是(
)
A.
B.
C.
D.
?
4.
、两条弧长相等,弧所对的圆心角是弧所对圆心角的一半,则弧所在圆的半径与弧所圆的半径之间的关系是(
)
A.
B.
C.
D.无法确定
?
5.
如图,是一个圆锥形冰激凌,已知它的母线长是,高是,则这个圆锥形冰激凌的底面面积是(
)
A.
B.
C.
D.
?
6.
如图,以为直径,点为圆心的半圆经过点,若,则图中阴影部分的面积是(?
?
?
?
)
A.
B.
C.
D.
?
7.
在半径为的圆中,的圆心角所对的弧长是(
)
A.
B.
C.
D.
?
8.
若圆锥的侧面展开图的弧长为,则此圆锥底面的半径为
.
A.
B.
C.
D.
?
9.
一个圆锥的底面周长是,高,沿直径把它切成相等的两半,表面积增加了?
?
?
??.(取)
A.
B.
C.
D.
?
10.
用一张面积为的正方形硬纸片围成一个圆柱的侧面,则这个圆柱的底面直径为(
)(不计接缝,精确到)
A.
B.
C.
D.
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
,
)
?
11.
如果圆柱的母线长为,底面半径为,那么这个圆柱的侧面积是________.
?
12.
已知扇形的圆心角为,面积为,则扇形弧长为________.
?
13.
在半径为的圆中,的圆心角所对的弧长等于________.
?
14.
半径为,圆心角为的扇形的面积为________.
?
15.
如图,若四边形是半径为厘米和的内接正方形,则图中四个弓形(即四个阴影部分)的面积之和为________厘米.
?
16.
如图,将一块实心三角板和实心半圆形量角器按图中方式叠放,三角板一直角边与量角器的零刻度线所在直线重合,斜边与半圆相切,重叠部分的量角器弧对应的圆心角为,的长为,则三角板和量角器重叠部分的面积为________.
?17.
用一块圆心角为的扇形铁皮,做一个高为的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是________.
?
18.
将半径为的圆形纸片沿折叠后,圆弧恰好能经过圆心,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为________.
三、
解答题
(本题共计
6小题
,共计66分
,
)
?
19.
如图,一个圆锥的高是厘米,侧面展开图是半圆,求圆锥的面积.
?
20.
如图,已知每个小正方形的边长为,,,都在小正方形顶点上,扇形是某个圆锥的侧面展开图.
计算这个圆锥侧面展开图的面积;
求这个圆锥的底面半径.
?
21.
某商店要制作圣诞节的圆锥形纸帽,已知纸帽的底面周长为,高为,要制作个这样的帽子要用多少平方厘米的纸?
?
22.
如图,,,以为直径画半圆交于,如果图中①的面积为,求阴影部分的面积.
?
23.
如图,圆锥的底面半径为,高为,求这个圆锥的侧面积和表面积.
?
?24.
如图是某学校田径体育场一部分的示意图,第一条跑道每圈为米,跑道分直道和弯道,直道为长相等的平行线段,弯道为同心的半圆型,弯道与直道相连接,已知直道的长米,跑道的宽为米.,结果精确到
(1)求第一条跑道的弯道部分的半径.
(2)求一圈中第二条跑道比第一条跑道长多少米?
(3)若进行米比赛,求第六道的起点与圆心的连线与的夹角的度数.
参考答案与试题解析
一、
选择题
(本题共计
10
小题
,每题
3
分
,共计30分
)
1.
【答案】
B
2.
【答案】
B
3.
【答案】
B
4.
【答案】
C
5.
【答案】
B
6.
【答案】
A
7.
【答案】
A
8.
【答案】
C
9.
【答案】
C
10.
【答案】
C
二、
填空题
(本题共计
8
小题
,每题
3
分
,共计24分
)
11.
【答案】
12.
【答案】
13.
【答案】
14.
【答案】
15.
【答案】
16.
【答案】
17.
【答案】
18.
【答案】
、
三、
解答题
(本题共计
7
小题
,每题
10
分
,共计70分
)
19.
【答案】
解:设圆锥底面圆的半径为,母线长为,
,所以,
在中,
∵
,
∴
,,
∴
,
∴
圆锥的面积.
20.
【答案】
解:由图可知,,
则弧的长为,
∴
面积为:.
设底面半径为,
则,
.
答:这个圆锥的底面半径为.
21.
【答案】
解:∵
纸帽的底面周长为,
∴
底面半径为:,
∴
母线长为:,
∴
一个圆锥形纸帽侧面积为:,
∴
要制作个这样的帽子要用平方厘米的纸.
22.
【答案】
解:设,
∵
,
∴
,
∵
,
∴
,
,
∴
图中①的面积.
23.
【答案】
解:∵
圆锥的底面半径为,高为,
∴
圆锥的母线长为,
∴
.
∵
圆锥的底面积,
∴
.
24.
【答案】
这个圆锥漏斗的侧面积是.
侧面展开图所对的圆心角是.
25.
【答案】
解:(1)弯道的半圆周长为(米),
由圆周长,所以半圆弧长
则第一道弯道部分的半径
(2)第二道与第一道的直跑道长相等,第二道与第一道的弯跑道的半径之差为米,第二道与第一道的弯跑道长的差即为两圆周长之差,即(米).
(3)从第一跑道米,是以点为始点,第六跑道上的运动员需要跑米的直道和米的弯道,即弧长为米,又第六道弯道半圆的半径为米,
由弧长与半圆,圆心角的关系得:,
所以.
同课章节目录
