人教版九年级数学上册24.1 圆心角与圆周角学案(无答案)
文档属性
| 名称 | 人教版九年级数学上册24.1 圆心角与圆周角学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 465.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 10:55:13 | ||
图片预览


文档简介
第一讲
弧、弦、圆心角
一、知识点梳理
1.顶点在_
的角叫做圆心角,能够重合的圆叫做
_;能够
的弧叫做等弧;圆绕其圆心旋转任意角度都能够与原来的图形重合,这就是圆的
.
2.在同圆或等圆中,相等的圆心角所对的弧
,所对的弦也
.
3.在同圆或等圆中,两个_
,两条
,两条
中有一组量相等,它们所对应的其余各组量也相等.
4.在⊙O中,AB,CD是两条弦,
(1)如果AB=CD,那么_
,
;
(2)如果=,那么
,
;
(3)如果∠AOB=∠COD,那么
,
.
二、同步题型分析
1.⊙O中,一条弦AB所对的劣弧为圆周的,则弦AB所对的圆心角为
.
2.在半径为2的⊙O中,圆心O到弦AB的距离为1,则弦AB所对的圆心角的度数为
.
3.如图,AD是⊙O的直径,AB=AC,∠CAB=120°,根据以上条件写出三个正确结论.(半径相等除外)
(1)
;
(2)_
_;
(3)
.
4.如图,在⊙O中,=,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
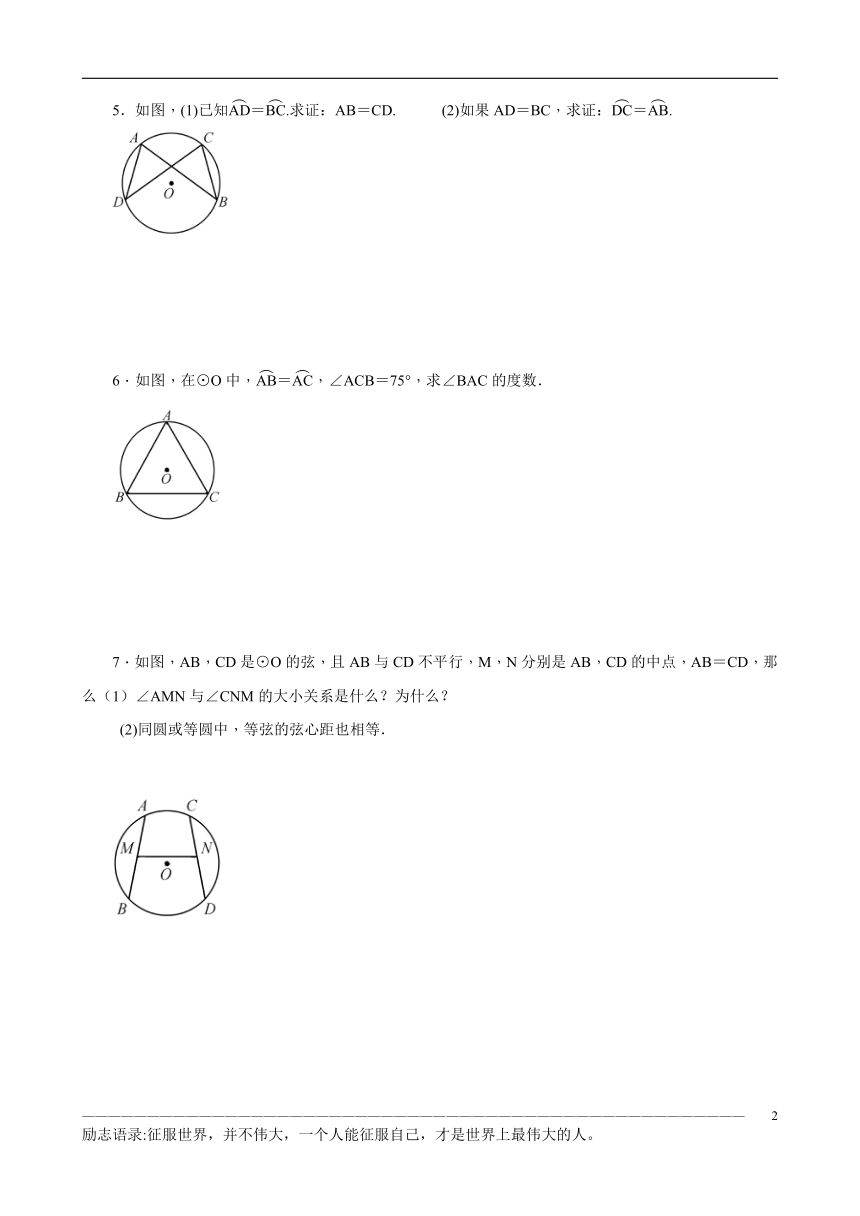
5.如图,(1)已知=.求证:AB=CD.
(2)如果AD=BC,求证:=.
6.如图,在⊙O中,=,∠ACB=75°,求∠BAC的度数.
7.如图,AB,CD是⊙O的弦,且AB与CD不平行,M,N分别是AB,CD的中点,AB=CD,那么(1)∠AMN与∠CNM的大小关系是什么?为什么?
(2)同圆或等圆中,等弦的弦心距也相等.
8.如图,AB是⊙O的直径,==,∠COD=35°,求∠AOE的度数.
9.如图所示,CD为⊙O的弦,在CD上截取CE=DF,连接OE,OF,它们的延长线交⊙O于点A,B.(1)试判断△OEF的形状,并说明理由;
(2)求证:=.
10.已知:如图,AB是⊙O的直径,M,N是AO,BO的中点.CM⊥AB,DN⊥AB,分别与圆交于C,D点.求证:=.
第二讲
圆周角
一、知识点梳理
1.顶点在
上,并且两边都与圆
的角叫做圆周角.
2.在同圆或等圆中,
或
所对的圆周角相等,都等于这条弧所对的
的一半.
3.在同圆或等圆中,相等的圆周角所对的弧也
4.半圆(或直径)所对的圆周角是
,90°的圆周角所对的弦是
.
5.圆内接四边形的对角
.
二、同步题型分析
1.如图1所示,点A,B,C在⊙O上,连接OA,OB,若∠ABO=25°,则∠C=
.
图1
图2
图3
图4
2.如图2所示,AB是⊙O的直径,AC是弦,若∠ACO=32°,则∠COB=
.
3.如图3所示,OA为⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,若OD=5
cm,则BE=
.
4.如图4所示,点A,B,C在⊙O上,已知∠B=60°,则∠CAO=
.
5.如图所示,点A,B,C,D在圆周上,∠A=65°,求∠D的度数.
5.如图所示,已知圆心角∠BOC=100°,点A为优弧上一点,求圆周角∠BAC的度数.
7.如图所示,在⊙O中,∠AOB=100°,C为优弧AB的中点,求∠CAB的度数.
8.如图所示,已知AB是⊙O的直径,∠BAC=32°,D是AC的中点,那么∠DAC
的度数是多少?
9.如图,⊙O的直径AB为10
cm,弦AC为6
cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
10.OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC.
11.如图,在⊙O中,∠CBD=30°,∠BDC=20°,求∠A.
PAGE
6
———————————————————————————————————————————————————
励志语录:征服世界,并不伟大,一个人能征服自己,才是世界上最伟大的人。
弧、弦、圆心角
一、知识点梳理
1.顶点在_
的角叫做圆心角,能够重合的圆叫做
_;能够
的弧叫做等弧;圆绕其圆心旋转任意角度都能够与原来的图形重合,这就是圆的
.
2.在同圆或等圆中,相等的圆心角所对的弧
,所对的弦也
.
3.在同圆或等圆中,两个_
,两条
,两条
中有一组量相等,它们所对应的其余各组量也相等.
4.在⊙O中,AB,CD是两条弦,
(1)如果AB=CD,那么_
,
;
(2)如果=,那么
,
;
(3)如果∠AOB=∠COD,那么
,
.
二、同步题型分析
1.⊙O中,一条弦AB所对的劣弧为圆周的,则弦AB所对的圆心角为
.
2.在半径为2的⊙O中,圆心O到弦AB的距离为1,则弦AB所对的圆心角的度数为
.
3.如图,AD是⊙O的直径,AB=AC,∠CAB=120°,根据以上条件写出三个正确结论.(半径相等除外)
(1)
;
(2)_
_;
(3)
.
4.如图,在⊙O中,=,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
5.如图,(1)已知=.求证:AB=CD.
(2)如果AD=BC,求证:=.
6.如图,在⊙O中,=,∠ACB=75°,求∠BAC的度数.
7.如图,AB,CD是⊙O的弦,且AB与CD不平行,M,N分别是AB,CD的中点,AB=CD,那么(1)∠AMN与∠CNM的大小关系是什么?为什么?
(2)同圆或等圆中,等弦的弦心距也相等.
8.如图,AB是⊙O的直径,==,∠COD=35°,求∠AOE的度数.
9.如图所示,CD为⊙O的弦,在CD上截取CE=DF,连接OE,OF,它们的延长线交⊙O于点A,B.(1)试判断△OEF的形状,并说明理由;
(2)求证:=.
10.已知:如图,AB是⊙O的直径,M,N是AO,BO的中点.CM⊥AB,DN⊥AB,分别与圆交于C,D点.求证:=.
第二讲
圆周角
一、知识点梳理
1.顶点在
上,并且两边都与圆
的角叫做圆周角.
2.在同圆或等圆中,
或
所对的圆周角相等,都等于这条弧所对的
的一半.
3.在同圆或等圆中,相等的圆周角所对的弧也
4.半圆(或直径)所对的圆周角是
,90°的圆周角所对的弦是
.
5.圆内接四边形的对角
.
二、同步题型分析
1.如图1所示,点A,B,C在⊙O上,连接OA,OB,若∠ABO=25°,则∠C=
.
图1
图2
图3
图4
2.如图2所示,AB是⊙O的直径,AC是弦,若∠ACO=32°,则∠COB=
.
3.如图3所示,OA为⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,若OD=5
cm,则BE=
.
4.如图4所示,点A,B,C在⊙O上,已知∠B=60°,则∠CAO=
.
5.如图所示,点A,B,C,D在圆周上,∠A=65°,求∠D的度数.
5.如图所示,已知圆心角∠BOC=100°,点A为优弧上一点,求圆周角∠BAC的度数.
7.如图所示,在⊙O中,∠AOB=100°,C为优弧AB的中点,求∠CAB的度数.
8.如图所示,已知AB是⊙O的直径,∠BAC=32°,D是AC的中点,那么∠DAC
的度数是多少?
9.如图,⊙O的直径AB为10
cm,弦AC为6
cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
10.OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC.求证:∠ACB=2∠BAC.
11.如图,在⊙O中,∠CBD=30°,∠BDC=20°,求∠A.
PAGE
6
———————————————————————————————————————————————————
励志语录:征服世界,并不伟大,一个人能征服自己,才是世界上最伟大的人。
同课章节目录
