沪科版(2012)初中数学八年级上册15.2 线段的垂直平分线 课件(共17张ppt)
文档属性
| 名称 | 沪科版(2012)初中数学八年级上册15.2 线段的垂直平分线 课件(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 965.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 11:53:40 | ||
图片预览





文档简介
(共17张PPT)
15.2.1
线段的垂直平分线
15.2.1
线段的垂直平分线
王伟
15.2.1
线段的垂直平分线
学习目标:
1、会用尺规作已知线段的垂直平分线
2、探究并理解线段垂直平分线的性质
3、能够运用垂直平分线的性质解决简单问题
重点:
掌握线段垂直平分线的性质。
难点:
能够利用直尺和圆规作已知线段的垂直平分线。
问题引入:
1、
什么是线段的垂直平分线?
2、你知道几种方法可以得到线段的垂直平分线?
3、你会画线段的垂直平分线吗?
4、
“线段的垂直平分线上的点到这条线段的两个端点的距离相等”你能证明这一结论吗?
M
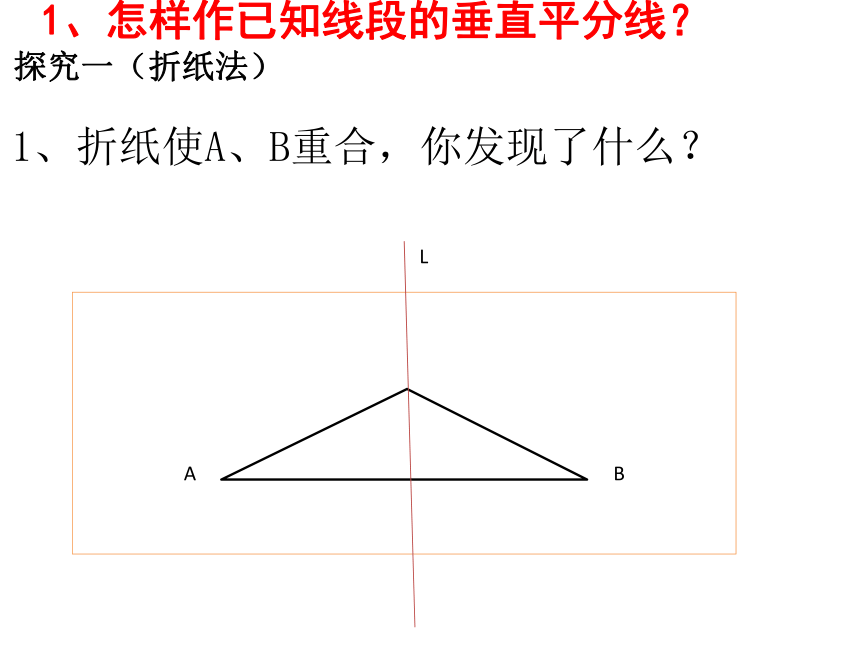
1、怎样作已知线段的垂直平分线?
探究一(折纸法)
1、折纸使A、B重合,你发现了什么?
L
B
A
探究二(刻度尺、三角板画法)
2、用刻度尺量出线段的中点,再用三角板画已知线段的垂直平分线。
驶向胜利的彼岸
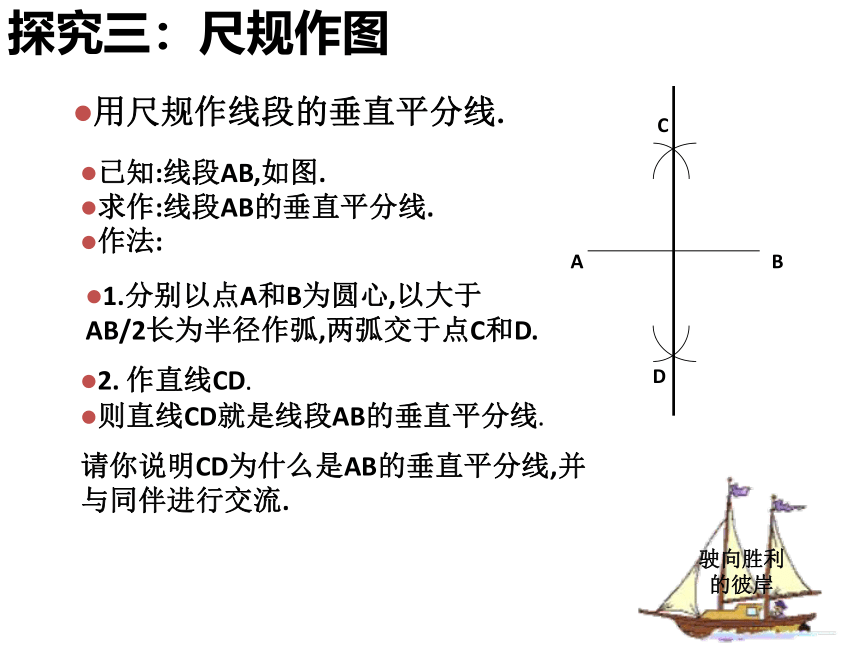
探究三:尺规作图
已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:
用尺规作线段的垂直平分线.
1.分别以点A和B为圆心,以大于AB/2长为半径作弧,两弧交于点C和D.
A
B
C
D
2.
作直线CD.
则直线CD就是线段AB的垂直平分线.
请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.
我们可以证明这样作出来的直线是符
合要求的,即证明直线CD垂直平分线
段AB.
如右图,连结CA、CB、
DA、DB,
∵
AC=BC,
AD=BD,CD=CD,
∴
△
≌△
(S.S.S.),
∴
∠ACD=∠BCD(全等三角形的对应角相等),
∴
CD垂直平分线段AB(等腰三角形“三线合一”).
由于直线CD与线段AB的交点就是AB的中点,因此我们可以用这种方法作出线段AB的中点,从而也可以作出任意一个三角形的三条中线.
A
B
线段的垂直平分线
PA=PB
P1
P1A=P1B
……
命题:线段垂直平分线上的点到这条线段两个端点的距离相等。
P
C
D
O
动手操作:作线段AB的垂直平分线CD,垂足为O;在CD上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
命题:线段垂直平分线上的点到这条线段两个端点的距离相等。
线段的垂直平分线
A
B
P
M
N
C
PA=PB
直线MN⊥AB,垂足为C,
且AC=CB.
已知:如图,
点P在MN上.
求证:
证明:∵MN⊥AB
∴
∠
PCA=
∠
PCB=90度
在
ΔPAC和Δ
PBC中,
AC=BC
∠
PCA=
∠
PCB
PC=PC
∴
ΔPAC
≌
Δ
PBC
∴PA=PB
性质定理:线段垂直平分线上的点到这条线段两个端点的
距离相等。
线段的垂直平分线
A
B
P
M
N
C
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
几何语言叙述:
∵点P在线段AB的垂直平分线上
∴
PA=PB
104
国
道
A
B
L
实际问题应用
在104国道L(济南—泰安段)的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?
线段的垂直平分线
2、如图,在直线L上求作一点P,使PA=PB.
L
A
B
实际问题
数学化
实际问题应用
p
PA=PB
数学问题源于生活实践,反过来数学又为生活实践服务
三、例题展示:?
如图:在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB.BC延长线于F.E
求证:(1)∠EAD=∠EDA
(2)DF∥AC
小结反思
1、本节课你学习了哪些知识?
2、你对本节课还有哪些困惑?
四、课堂检测:??
1、已知:线段AB及一点P,PA=PB,则点P在
上.
2、
△ABC中,∠A=50度,AB=AC,AB的垂直平分线交AC于D则∠DBC的度数
.
3、在△ABC中,AB=AC=17,BC=16,DE垂直平分AB,则△BCD的周长是??????
。
4、有特大城市A及两个小城市B、C,这三个城市共建一个污水处理厂,使得该厂到B、C两城市的距离相等,且使A市到厂的管线最短,试确定污水处理厂的位置。
5、如图,已知△ABC,请用直尺和圆规作图,将三角形分成面积相等的两部分。
?
C
B
A
作业:
1、教材P131
,习题15.2第一题、第二题。
2、完成对应的同步练习。
15.2.1
线段的垂直平分线
15.2.1
线段的垂直平分线
王伟
15.2.1
线段的垂直平分线
学习目标:
1、会用尺规作已知线段的垂直平分线
2、探究并理解线段垂直平分线的性质
3、能够运用垂直平分线的性质解决简单问题
重点:
掌握线段垂直平分线的性质。
难点:
能够利用直尺和圆规作已知线段的垂直平分线。
问题引入:
1、
什么是线段的垂直平分线?
2、你知道几种方法可以得到线段的垂直平分线?
3、你会画线段的垂直平分线吗?
4、
“线段的垂直平分线上的点到这条线段的两个端点的距离相等”你能证明这一结论吗?
M
1、怎样作已知线段的垂直平分线?
探究一(折纸法)
1、折纸使A、B重合,你发现了什么?
L
B
A
探究二(刻度尺、三角板画法)
2、用刻度尺量出线段的中点,再用三角板画已知线段的垂直平分线。
驶向胜利的彼岸
探究三:尺规作图
已知:线段AB,如图.
求作:线段AB的垂直平分线.
作法:
用尺规作线段的垂直平分线.
1.分别以点A和B为圆心,以大于AB/2长为半径作弧,两弧交于点C和D.
A
B
C
D
2.
作直线CD.
则直线CD就是线段AB的垂直平分线.
请你说明CD为什么是AB的垂直平分线,并与同伴进行交流.
我们可以证明这样作出来的直线是符
合要求的,即证明直线CD垂直平分线
段AB.
如右图,连结CA、CB、
DA、DB,
∵
AC=BC,
AD=BD,CD=CD,
∴
△
≌△
(S.S.S.),
∴
∠ACD=∠BCD(全等三角形的对应角相等),
∴
CD垂直平分线段AB(等腰三角形“三线合一”).
由于直线CD与线段AB的交点就是AB的中点,因此我们可以用这种方法作出线段AB的中点,从而也可以作出任意一个三角形的三条中线.
A
B
线段的垂直平分线
PA=PB
P1
P1A=P1B
……
命题:线段垂直平分线上的点到这条线段两个端点的距离相等。
P
C
D
O
动手操作:作线段AB的垂直平分线CD,垂足为O;在CD上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
命题:线段垂直平分线上的点到这条线段两个端点的距离相等。
线段的垂直平分线
A
B
P
M
N
C
PA=PB
直线MN⊥AB,垂足为C,
且AC=CB.
已知:如图,
点P在MN上.
求证:
证明:∵MN⊥AB
∴
∠
PCA=
∠
PCB=90度
在
ΔPAC和Δ
PBC中,
AC=BC
∠
PCA=
∠
PCB
PC=PC
∴
ΔPAC
≌
Δ
PBC
∴PA=PB
性质定理:线段垂直平分线上的点到这条线段两个端点的
距离相等。
线段的垂直平分线
A
B
P
M
N
C
PA=PB
点P在线段AB的垂直平分线上
线段垂直平分线上的点到这条线段两个端点的距离相等
几何语言叙述:
∵点P在线段AB的垂直平分线上
∴
PA=PB
104
国
道
A
B
L
实际问题应用
在104国道L(济南—泰安段)的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂的工人都没意见,问医院的院址应选在何处?
线段的垂直平分线
2、如图,在直线L上求作一点P,使PA=PB.
L
A
B
实际问题
数学化
实际问题应用
p
PA=PB
数学问题源于生活实践,反过来数学又为生活实践服务
三、例题展示:?
如图:在△ABC中,AD是∠BAC平分线,AD的垂直平分线分别交AB.BC延长线于F.E
求证:(1)∠EAD=∠EDA
(2)DF∥AC
小结反思
1、本节课你学习了哪些知识?
2、你对本节课还有哪些困惑?
四、课堂检测:??
1、已知:线段AB及一点P,PA=PB,则点P在
上.
2、
△ABC中,∠A=50度,AB=AC,AB的垂直平分线交AC于D则∠DBC的度数
.
3、在△ABC中,AB=AC=17,BC=16,DE垂直平分AB,则△BCD的周长是??????
。
4、有特大城市A及两个小城市B、C,这三个城市共建一个污水处理厂,使得该厂到B、C两城市的距离相等,且使A市到厂的管线最短,试确定污水处理厂的位置。
5、如图,已知△ABC,请用直尺和圆规作图,将三角形分成面积相等的两部分。
?
C
B
A
作业:
1、教材P131
,习题15.2第一题、第二题。
2、完成对应的同步练习。
