沪科版(2012)初中数学八年级上册15.2 线段的垂直平分线 课件(共20张ppt)
文档属性
| 名称 | 沪科版(2012)初中数学八年级上册15.2 线段的垂直平分线 课件(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 197.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 11:55:22 | ||
图片预览







文档简介
(共20张PPT)
15.2
线段的垂直平分线
濉溪县开通了乡村公交,政府准备出资在公路边修建一个站台,公路的同侧有A,B两村。试问,该站台修建在哪里?
A
B
怎么办?
·
·
公路
怎样才能使它到A,B
两村的距离相等?
学习目标
1、会用尺规作图作一条线段的垂直平分线,并能证明它的正确性。
2、理解线段垂直平分线的性质定理并能予以证明。
3、能利用线段的垂直平分线的性质定理解决问题。
1、什么是线段的垂直平分线?
复习回顾
经过线段的中点,并且垂直于这条线段的直线叫做这条线段的垂直平分线。又叫做中垂线。
动动手:
在半透明纸上画一条线段AB,折纸使A与B重合,得到的折痕l就是线段AB的垂直平分线.
想一想:
这样折纸怎么就是垂直平分线呢?
A
B
A(B)
l
O
新课教学
1、如何作出线段的垂直平分线?
2、如果用直尺和圆规,能画出线段的垂直平分线吗?
交流与探究
自学课本128页的尺规作图,并思考以下问题:
1、作线段的垂直平分线需要几步?
2、为什么要以大于
AB长为半径呢?
A
B
C
D
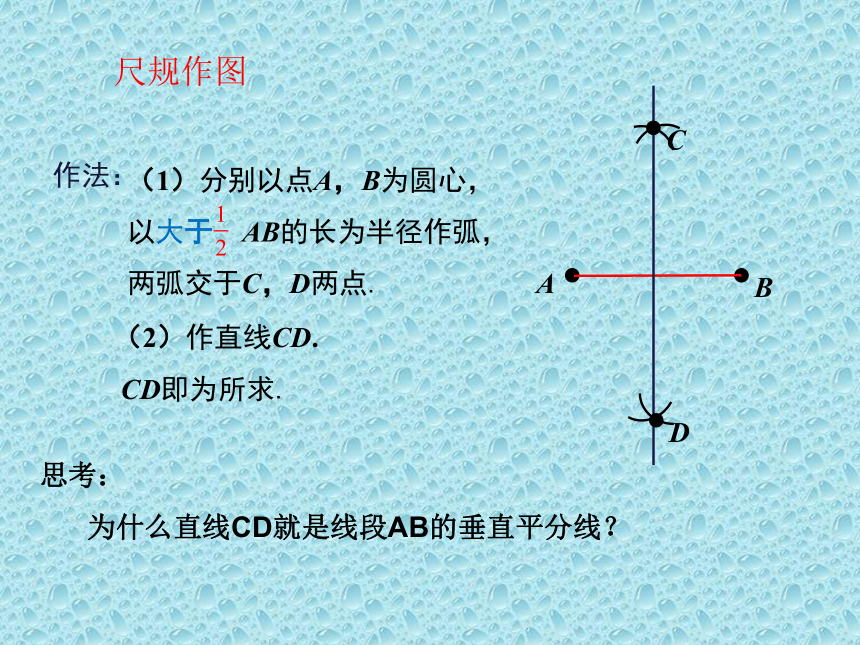
作法:
(1)分别以点A,B为圆心,以大于
AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
思考:
为什么直线CD就是线段AB的垂直平分线?
尺规作图
A
B
PA=PB
P1
P1A=P1B
……
P
M
N
O
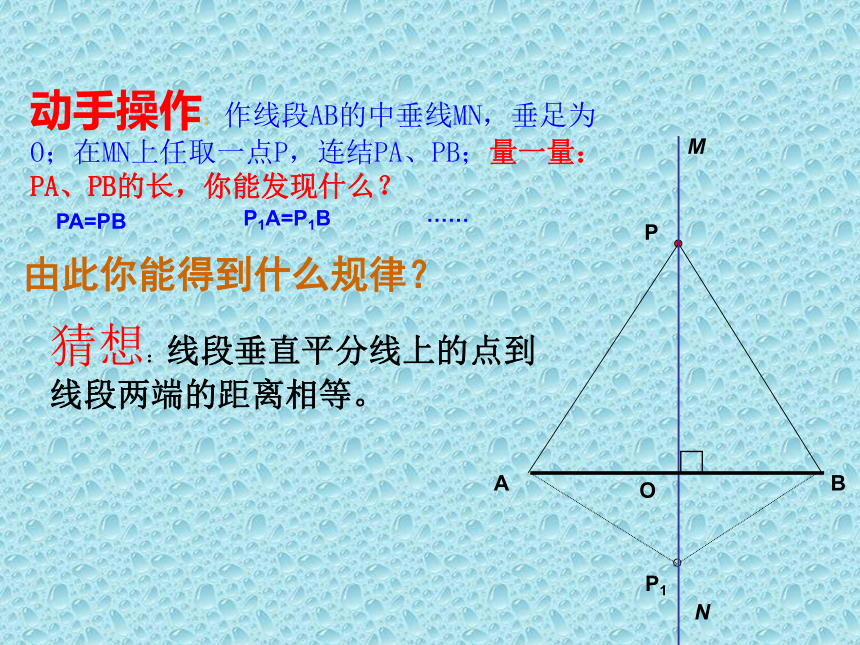
动手操作:作线段AB的中垂线MN,垂足为O;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
猜想:线段垂直平分线上的点到线段两端的距离相等。
性质定理:线段垂直平分线上的点到线段两端的距离相等。
线段的垂直平分线
几何语言:
∵点P在AB的垂直平分线上
∴PA=PB
_
B
_
A
l
P
o
结合以上内容,
从图形中你还能得到什么?
_
B
_
A
l
P
o
1、如图1所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为(
)
A.
6
B.
5
C.
4
D.
3
B
P
A
B
C
D
图1
针对性训练
2、已知,如图,y轴垂直平分线段BC,点A在y轴上,点B、C在x轴上。
(1)若点C的坐标为(3,0),则点B的坐标是__________;
(2)若点B的坐标为(m,0),则点C的坐标是________。
(-3,0)
(-m,0)
针对性训练
3.如图,△ABC中,AD垂直平分BC,
已知△ABC的周长为36,△ABD的
周长为28,则AD长为
.
A
B
C
D
10
针对性训练
如图,四边形ABCD中,直线AC垂直平分BD于点O。
(1)图中有多少对全等三
角形,请把它们写出来;
(2)任选(1)中一对全等
三角形加以证明。
针对性训练
濉溪县开通了乡村公交,政府准备出资在公路边修建一个站台,试问,该站台修建在哪里,才能使它到位于公路同侧的A,B
两村的距离相等。
A
B
解决问题
·
·
公路
P.
∴站台应建在P点
理论依据是:
公路
实际问题
数学化
→
A
B
L
如图,在直线L上求作一点P,使PA=PB.
这节课我们主要学习了……
小结:
作业布置
必做题:习题15.2第2、3题。
选做题:在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.
谢谢!
15.2
线段的垂直平分线
濉溪县开通了乡村公交,政府准备出资在公路边修建一个站台,公路的同侧有A,B两村。试问,该站台修建在哪里?
A
B
怎么办?
·
·
公路
怎样才能使它到A,B
两村的距离相等?
学习目标
1、会用尺规作图作一条线段的垂直平分线,并能证明它的正确性。
2、理解线段垂直平分线的性质定理并能予以证明。
3、能利用线段的垂直平分线的性质定理解决问题。
1、什么是线段的垂直平分线?
复习回顾
经过线段的中点,并且垂直于这条线段的直线叫做这条线段的垂直平分线。又叫做中垂线。
动动手:
在半透明纸上画一条线段AB,折纸使A与B重合,得到的折痕l就是线段AB的垂直平分线.
想一想:
这样折纸怎么就是垂直平分线呢?
A
B
A(B)
l
O
新课教学
1、如何作出线段的垂直平分线?
2、如果用直尺和圆规,能画出线段的垂直平分线吗?
交流与探究
自学课本128页的尺规作图,并思考以下问题:
1、作线段的垂直平分线需要几步?
2、为什么要以大于
AB长为半径呢?
A
B
C
D
作法:
(1)分别以点A,B为圆心,以大于
AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
思考:
为什么直线CD就是线段AB的垂直平分线?
尺规作图
A
B
PA=PB
P1
P1A=P1B
……
P
M
N
O
动手操作:作线段AB的中垂线MN,垂足为O;在MN上任取一点P,连结PA、PB;量一量:PA、PB的长,你能发现什么?
由此你能得到什么规律?
猜想:线段垂直平分线上的点到线段两端的距离相等。
性质定理:线段垂直平分线上的点到线段两端的距离相等。
线段的垂直平分线
几何语言:
∵点P在AB的垂直平分线上
∴PA=PB
_
B
_
A
l
P
o
结合以上内容,
从图形中你还能得到什么?
_
B
_
A
l
P
o
1、如图1所示,直线CD是线段AB的垂直平分线,点P为直线CD上的一点,且PA=5,则线段PB的长为(
)
A.
6
B.
5
C.
4
D.
3
B
P
A
B
C
D
图1
针对性训练
2、已知,如图,y轴垂直平分线段BC,点A在y轴上,点B、C在x轴上。
(1)若点C的坐标为(3,0),则点B的坐标是__________;
(2)若点B的坐标为(m,0),则点C的坐标是________。
(-3,0)
(-m,0)
针对性训练
3.如图,△ABC中,AD垂直平分BC,
已知△ABC的周长为36,△ABD的
周长为28,则AD长为
.
A
B
C
D
10
针对性训练
如图,四边形ABCD中,直线AC垂直平分BD于点O。
(1)图中有多少对全等三
角形,请把它们写出来;
(2)任选(1)中一对全等
三角形加以证明。
针对性训练
濉溪县开通了乡村公交,政府准备出资在公路边修建一个站台,试问,该站台修建在哪里,才能使它到位于公路同侧的A,B
两村的距离相等。
A
B
解决问题
·
·
公路
P.
∴站台应建在P点
理论依据是:
公路
实际问题
数学化
→
A
B
L
如图,在直线L上求作一点P,使PA=PB.
这节课我们主要学习了……
小结:
作业布置
必做题:习题15.2第2、3题。
选做题:在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;
(2)AB=BC+AD.
谢谢!
