华东师大版数学九年级下册27.4 正多边形和圆课件(共22张PPT)
文档属性
| 名称 | 华东师大版数学九年级下册27.4 正多边形和圆课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 12:24:02 | ||
图片预览






文档简介
(共22张PPT)
正多边形和圆
第27章
圆
华东师大版九年级下册
观
察
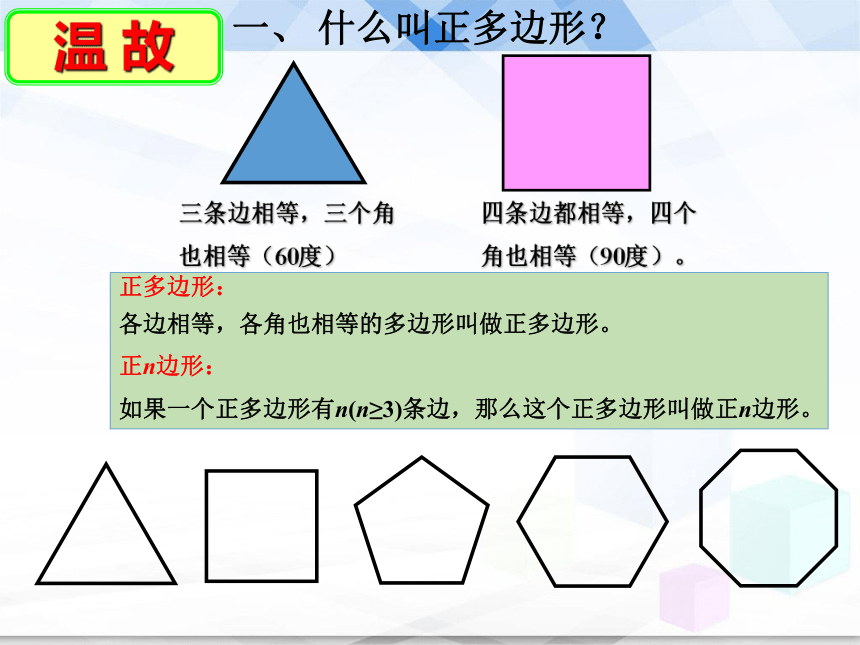
正多边形:
各边相等,各角也相等的多边形叫做正多边形。
正n边形:
如果一个正多边形有n(n≥3)条边,那么这个正多边形叫做正n边形。
三条边相等,三个角也相等(60度)
四条边都相等,四个角也相等(90度)。
温
故
一、
什么叫正多边形?
1、菱形是正多边形吗?为什么?
考考你!
2、矩形是正多边形吗?为什么?
3、正方形是正多边形吗?为什么?
二、
正多边形有没有外接圆、内切圆?
正多边形和圆有什么关系?
探
知1
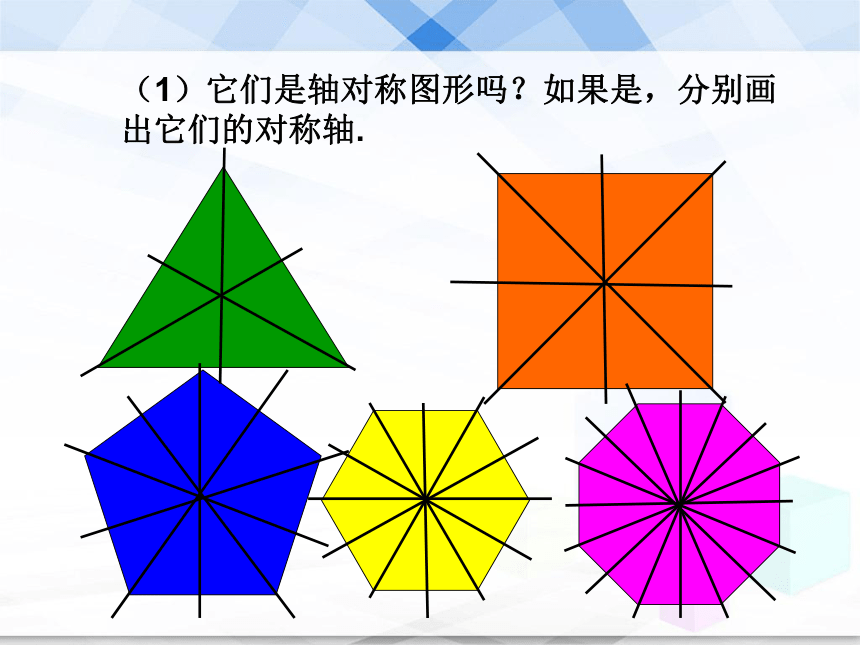
(1)它们是轴对称图形吗?如果是,分别画出它们的对称轴.
(2)它们分别有多少条对称轴?数一数,你发现了什么规律?正n边形有多少条对称轴?
(3)正多边形的对称轴具有什么特点?
正多边形都是轴对称图形,
一个正n边形一共有
n条对称轴,这n条
对称轴相交于一点.
边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心。
新
知
正五边形:
有一个外接圆和一个内切圆。
任何正多边形:
都有一个外接圆和一个内切圆。
E
F
C
D
.
.
O
中心角
半径R
边心距r
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
A
B
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
探
知2
如图,A,B,C,D,E都是⊙
O上的点,且∠AOB=
∠BOC=∠COD=∠DOE.
(1)弦AB,BC,CD,DE的长相等吗?为什么?
(2)∠ABC,∠BCD,∠CDE相等吗?为什么?
(3)由(1)和(2),你能设计出画正n边形的方法吗?与同伴进行交流.
E
D
C
B
A
O
三、
怎样由圆得到一个正五边形?
O
A
B
C
D
E
1、五等分圆周;
2、顺次连接五个分点。
怎样证明它是正五边形?
做一做
用直尺和圆规作一个正六边形.
O
·
作法:(1)任意画一个圆,记圆心为O,如图所示:
(2)在⊙O上任取一点A,自点A起在⊙O上依次截取长度等于半径OA的弦,得到点B,C,D,E,F.
例1
O
A
B
C
E
F
·
D
(3)顺次连接点A,B,C,D,E,F,A,如图.
六边形ABCDEF就是所求的正六边形.
五、
如何画一个边长为2cm的正六边形?
O
A
B
C
D
E
F
1、以2cm为半径作一个⊙
O;
2、用量角器画一个60°的圆心角;
3、在圆上顺次截取这个圆心角对的弧;
4、顺次连接分点。
延伸拓展
用尺规作一个正三角形。
由此你还能作哪些正多边形?
练
习
通过本课的学习,你又有
什么收获?
回顾总结
1.正多边形和圆的有关概念
2.正多边形的基本图形
3.正多边形的画法
归纳总结
正多边形和圆
第27章
圆
华东师大版九年级下册
观
察
正多边形:
各边相等,各角也相等的多边形叫做正多边形。
正n边形:
如果一个正多边形有n(n≥3)条边,那么这个正多边形叫做正n边形。
三条边相等,三个角也相等(60度)
四条边都相等,四个角也相等(90度)。
温
故
一、
什么叫正多边形?
1、菱形是正多边形吗?为什么?
考考你!
2、矩形是正多边形吗?为什么?
3、正方形是正多边形吗?为什么?
二、
正多边形有没有外接圆、内切圆?
正多边形和圆有什么关系?
探
知1
(1)它们是轴对称图形吗?如果是,分别画出它们的对称轴.
(2)它们分别有多少条对称轴?数一数,你发现了什么规律?正n边形有多少条对称轴?
(3)正多边形的对称轴具有什么特点?
正多边形都是轴对称图形,
一个正n边形一共有
n条对称轴,这n条
对称轴相交于一点.
边数是偶数的正多边形还是中心对称图形,它的中心就是对称中心。
新
知
正五边形:
有一个外接圆和一个内切圆。
任何正多边形:
都有一个外接圆和一个内切圆。
E
F
C
D
.
.
O
中心角
半径R
边心距r
正多边形的中心:一个正多边形的外接圆的圆心.
正多边形的半径:外接圆的半径
正多边形的中心角:正多边形的每一条边所对的圆心角.
正多边形的边心距:
中心到正多边形的一边的距离.
A
B
E
F
C
D
.
.
O
中心角
A
B
G
边心距把△AOB分成
2个全等的直角三角形
设正多边形的边长为a,半径为R,它的周长为L=na.
R
a
探
知2
如图,A,B,C,D,E都是⊙
O上的点,且∠AOB=
∠BOC=∠COD=∠DOE.
(1)弦AB,BC,CD,DE的长相等吗?为什么?
(2)∠ABC,∠BCD,∠CDE相等吗?为什么?
(3)由(1)和(2),你能设计出画正n边形的方法吗?与同伴进行交流.
E
D
C
B
A
O
三、
怎样由圆得到一个正五边形?
O
A
B
C
D
E
1、五等分圆周;
2、顺次连接五个分点。
怎样证明它是正五边形?
做一做
用直尺和圆规作一个正六边形.
O
·
作法:(1)任意画一个圆,记圆心为O,如图所示:
(2)在⊙O上任取一点A,自点A起在⊙O上依次截取长度等于半径OA的弦,得到点B,C,D,E,F.
例1
O
A
B
C
E
F
·
D
(3)顺次连接点A,B,C,D,E,F,A,如图.
六边形ABCDEF就是所求的正六边形.
五、
如何画一个边长为2cm的正六边形?
O
A
B
C
D
E
F
1、以2cm为半径作一个⊙
O;
2、用量角器画一个60°的圆心角;
3、在圆上顺次截取这个圆心角对的弧;
4、顺次连接分点。
延伸拓展
用尺规作一个正三角形。
由此你还能作哪些正多边形?
练
习
通过本课的学习,你又有
什么收获?
回顾总结
1.正多边形和圆的有关概念
2.正多边形的基本图形
3.正多边形的画法
归纳总结
