华东师大版数学七年级上册-5.2.3 平行线的性质 课件(共25张ppt)
文档属性
| 名称 | 华东师大版数学七年级上册-5.2.3 平行线的性质 课件(共25张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 263.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 12:23:22 | ||
图片预览





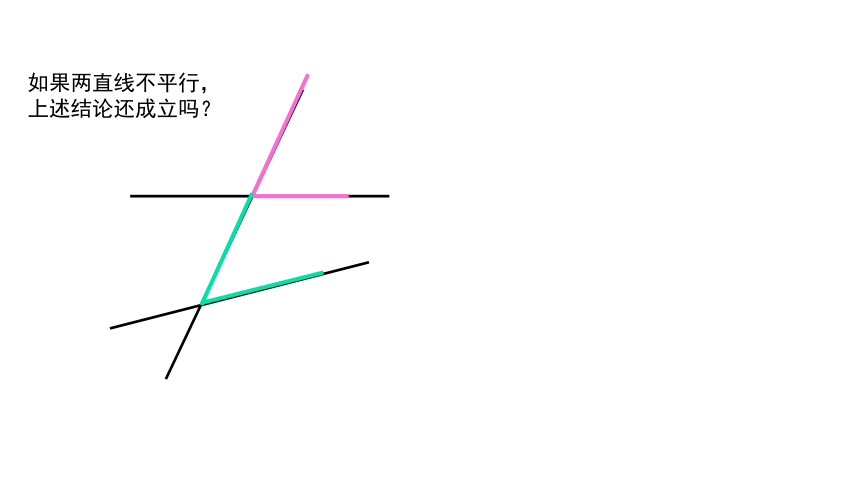

文档简介
(共25张PPT)
5.2.3平行线的性质
1.探索平行线的性质,并掌握平行线性质的图形语言、文字语言、符号语言.
2.了解平行线的性质与判定的区别。
3.通过学生动手操作、实验、观察,培养学生主动探索与合作的能力,使学生领会数形结合、转化
的数学思想和方法,从而提高学生分析问题和解决问题的能力。
重点:探究平行线的性质。
难点:明确平行线的性质与判定的区别。
学习目标:
一、导入新课。根据右图,填空:
①如果∠1=∠C,
那么__∥__(
)
②
如果∠1=∠B
那么__∥__(
)
③
如果∠2+∠B=180°,
那么__∥__(
)
E
A
C
D
B
1
2
3
4
想一想:
平行线的三种判定方法分别是
先知道什么……、
后得到什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
探究:如图两条平行线a//b,一条截线c与a、b相交,标出如图的角.
任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
利用同位角相等,或者内错角相等,或者同旁内角互补可以判定两条直线平行。反过来如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
二、平行线性质的探索和应用
思考:
a
b
c
1
3
2
4
8
5
7
6
观察
各对同位角、内错角、同旁内角的度数之间有什么关系?说出你的猜想:
猜想
两条平行线被第三条直线所截,同位角____,
内错角_____,同旁内角_____.
相等
相等
互补
a
b
d
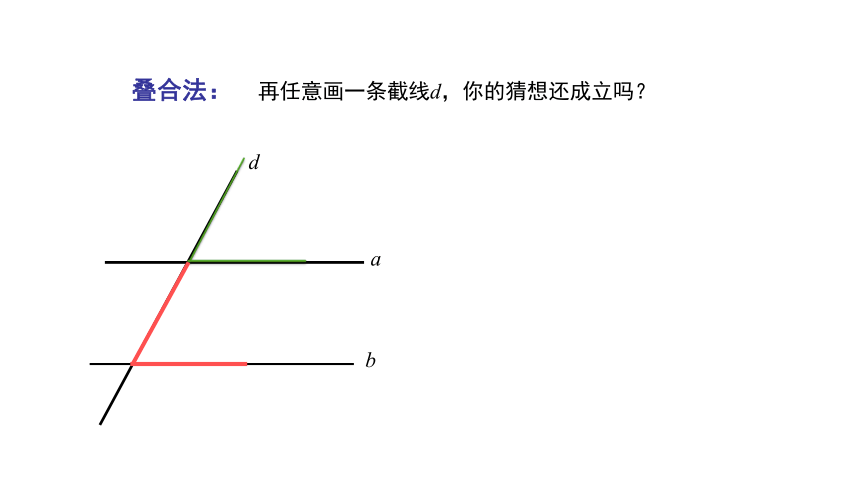
叠合法:
再任意画一条截线d,你的猜想还成立吗?
如果两直线不平行,
上述结论还成立吗?
一般地,平行线具有性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
总结归纳
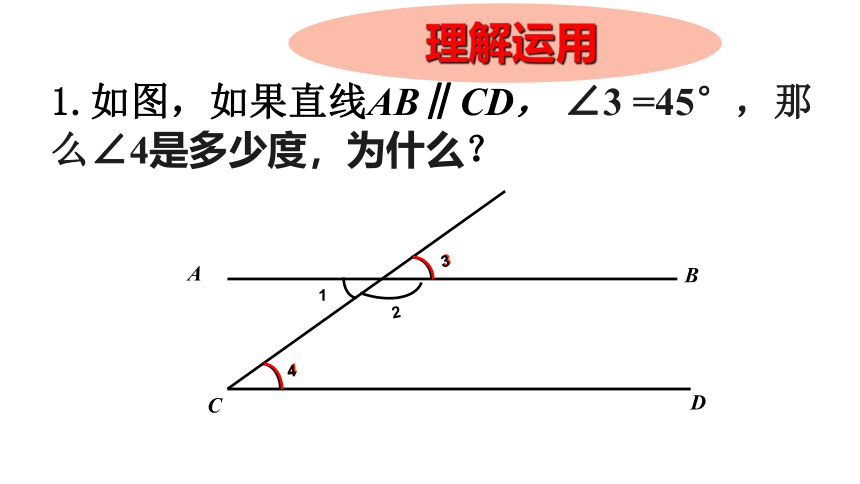
1.如图,如果直线AB∥CD,
∠3
=45°,那么∠4是多少度,为什么?
D
B
4
3
1
4
3
2
A
C
理解运用
思考1:
如图,已知a//b,那么?2与?3相等吗?为什么?
解∵
a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵
∠1=∠3(对顶角相等),
∴
∠2=∠3(等量代换).
b
1
2
a
c
3
性质2:两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
总结归纳
2.如果直线AB
∥CD,那么∠1
=∠2吗?
∠3
=∠2吗?为什么?
如果直线EF∥HG,∠5
=∠2吗?
为什么?
A
B
C
E
F
D
2
5
H
G
4
1
3
理解运用
思考2.如图,已知a//b,那么?2与?4有什么关系呢?为什么?
b
1
2
a
c
4
解:
∵a//b
(已知),
∴?
1=
?
2
(两直线平行,同位角相等).
∵
?
1+
?
4=180°
(邻补角定义),
∴?
2+
?
4=180°
(等量代换).
性质3:两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180
°
(两直线平行,同旁内角互补)
∵a∥b(已知)
应用格式:
总结归纳
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
已知条件
结论
已知条件
结论
例1
如图,是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
A
B
C
D
解:
∵AB
∥
CD(已知)
∴∠A+∠D=180°,∠B+∠C=180°
(两直线平行,同旁内角互补)
∴梯形的另外两个角分别是80°
、
65°.
∵
∠A=100°,∠B=115°
∴∠D=180
°-∠A=180°-100°=80°
∠C=
180
°-∠B=180°-115°=65°
三、典例分析
四、请分享你的收获
1.如图,一条公路两次拐弯前后两条路互相平行.第一次拐的角∠B是142゜,第二次
拐的角∠C是多少度?为什么?
B
C
解:∠C=142o
∵两直线平行,内错角相等.
五、课后练习
2.如图直线
a
∥
b,直线b垂直于直线c,则直线a垂直于直线c吗?
a
b
c
3.∠1
和∠2是两条直线被第三条直线所截形成的同旁内角,要使这两条直线平行,必须
(
)
A.
∠1=
∠2
B.
∠1+∠2=90o
C.
2(∠1+∠2)=360o
D
.∠1是钝角,
∠2是锐角
C
解:
∠A
=∠D.理由:
∵
AB∥DE(
)
∴∠A=_______
(
)
∵AC∥DF(
)
∴∠D=______
(
)
∴∠A=∠D
(
)
4.如图1,若AB∥DE
, AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。
P
F
C
E
B
A
D
图1
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
解:
∠A+∠D=180o.
理由:
∵
AB∥DE(
)
∴∠A=__________
(
)
∵AC∥DF(
)
∴∠D+
_______=180o
(
)
∴∠A+∠D=180o(
)
如图2,若AB∥DE
, AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
5.如图1,CE平分∠ACD,AE平分∠BAC,且∠EAC+∠ACE=90?.
(1)请判断AB与CD的位置关系,并说明理由;
(2)如图2,当∠E=90?且AB与CD的位置关系保持不变,当直角顶点E点移动时,写出∠BAE与∠ECD的数量关系,并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点,且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外),∠CPQ+∠CQP与∠BAC有何数量关系?写出结论,并加以证明.
六、课后作业
1、教材P178(1-5题)
2、做在书上,中午检查。
再见
5.2.3平行线的性质
1.探索平行线的性质,并掌握平行线性质的图形语言、文字语言、符号语言.
2.了解平行线的性质与判定的区别。
3.通过学生动手操作、实验、观察,培养学生主动探索与合作的能力,使学生领会数形结合、转化
的数学思想和方法,从而提高学生分析问题和解决问题的能力。
重点:探究平行线的性质。
难点:明确平行线的性质与判定的区别。
学习目标:
一、导入新课。根据右图,填空:
①如果∠1=∠C,
那么__∥__(
)
②
如果∠1=∠B
那么__∥__(
)
③
如果∠2+∠B=180°,
那么__∥__(
)
E
A
C
D
B
1
2
3
4
想一想:
平行线的三种判定方法分别是
先知道什么……、
后得到什么?
同位角相等
内错角相等
同旁内角互补
两直线平行
AB
CD
EC
BD
同位角相等,两直线平行
内错角相等,两直线平行
EC
BD
同旁内角互补,两直线平行
探究:如图两条平行线a//b,一条截线c与a、b相交,标出如图的角.
任选一组同位角、内错角或同旁内角,度量这些角,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
利用同位角相等,或者内错角相等,或者同旁内角互补可以判定两条直线平行。反过来如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
二、平行线性质的探索和应用
思考:
a
b
c
1
3
2
4
8
5
7
6
观察
各对同位角、内错角、同旁内角的度数之间有什么关系?说出你的猜想:
猜想
两条平行线被第三条直线所截,同位角____,
内错角_____,同旁内角_____.
相等
相等
互补
a
b
d
叠合法:
再任意画一条截线d,你的猜想还成立吗?
如果两直线不平行,
上述结论还成立吗?
一般地,平行线具有性质:
性质1:两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
b
1
2
a
c
∴∠1=∠2
(两直线平行,同位角相等)
∵a∥b(已知)
应用格式:
总结归纳
1.如图,如果直线AB∥CD,
∠3
=45°,那么∠4是多少度,为什么?
D
B
4
3
1
4
3
2
A
C
理解运用
思考1:
如图,已知a//b,那么?2与?3相等吗?为什么?
解∵
a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵
∠1=∠3(对顶角相等),
∴
∠2=∠3(等量代换).
b
1
2
a
c
3
性质2:两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等.
b
1
2
a
c
3
∴∠2=∠3
(两直线平行,内错角相等)
∵a∥b(已知)
应用格式:
总结归纳
2.如果直线AB
∥CD,那么∠1
=∠2吗?
∠3
=∠2吗?为什么?
如果直线EF∥HG,∠5
=∠2吗?
为什么?
A
B
C
E
F
D
2
5
H
G
4
1
3
理解运用
思考2.如图,已知a//b,那么?2与?4有什么关系呢?为什么?
b
1
2
a
c
4
解:
∵a//b
(已知),
∴?
1=
?
2
(两直线平行,同位角相等).
∵
?
1+
?
4=180°
(邻补角定义),
∴?
2+
?
4=180°
(等量代换).
性质3:两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补.
b
1
2
a
c
4
∴∠2+∠4=180
°
(两直线平行,同旁内角互补)
∵a∥b(已知)
应用格式:
总结归纳
两直线平行
同位角相等
内错角相等
同旁内角互补
平行线的判定
平行线的性质
线的关系
角的关系
性质
角的关系
线的关系
判定
讨论:平行线三个性质的条件是什么?结论是什么?它与判定有什么区别?(分组讨论)
已知条件
结论
已知条件
结论
例1
如图,是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
A
B
C
D
解:
∵AB
∥
CD(已知)
∴∠A+∠D=180°,∠B+∠C=180°
(两直线平行,同旁内角互补)
∴梯形的另外两个角分别是80°
、
65°.
∵
∠A=100°,∠B=115°
∴∠D=180
°-∠A=180°-100°=80°
∠C=
180
°-∠B=180°-115°=65°
三、典例分析
四、请分享你的收获
1.如图,一条公路两次拐弯前后两条路互相平行.第一次拐的角∠B是142゜,第二次
拐的角∠C是多少度?为什么?
B
C
解:∠C=142o
∵两直线平行,内错角相等.
五、课后练习
2.如图直线
a
∥
b,直线b垂直于直线c,则直线a垂直于直线c吗?
a
b
c
3.∠1
和∠2是两条直线被第三条直线所截形成的同旁内角,要使这两条直线平行,必须
(
)
A.
∠1=
∠2
B.
∠1+∠2=90o
C.
2(∠1+∠2)=360o
D
.∠1是钝角,
∠2是锐角
C
解:
∠A
=∠D.理由:
∵
AB∥DE(
)
∴∠A=_______
(
)
∵AC∥DF(
)
∴∠D=______
(
)
∴∠A=∠D
(
)
4.如图1,若AB∥DE
, AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。
P
F
C
E
B
A
D
图1
已知
∠CPE
两直线平行,同位角相等
已知
∠CPE
两直线平行,同位角相等
等量代换
解:
∠A+∠D=180o.
理由:
∵
AB∥DE(
)
∴∠A=__________
(
)
∵AC∥DF(
)
∴∠D+
_______=180o
(
)
∴∠A+∠D=180o(
)
如图2,若AB∥DE
, AC∥DF,请说出∠A和∠D之间的数量关系,并说明理由。
图2
F
C
E
B
A
D
P
已知
∠CPD
两直线平行,同位角相等
已知
∠CPD
两直线平行,同旁内角互补
等量代换
5.如图1,CE平分∠ACD,AE平分∠BAC,且∠EAC+∠ACE=90?.
(1)请判断AB与CD的位置关系,并说明理由;
(2)如图2,当∠E=90?且AB与CD的位置关系保持不变,当直角顶点E点移动时,写出∠BAE与∠ECD的数量关系,并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点,且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外),∠CPQ+∠CQP与∠BAC有何数量关系?写出结论,并加以证明.
六、课后作业
1、教材P178(1-5题)
2、做在书上,中午检查。
再见
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
