人教版 数学九年级上册 学案24.1圆的有关性质
文档属性
| 名称 | 人教版 数学九年级上册 学案24.1圆的有关性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 586.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 12:35:15 | ||
图片预览




文档简介
24.1
圆的有关性质
一、知识点过关
知识点1
圆的定义及其表示方法
(重点;理解)
【命题点1
圆的定义】
例1
下列说法中,错误的有
(
)
(1)经过点P的圆有无数个;
(2)以点P为圆心的圆有无数个;
(3)半径为且经过点P的圆有无数个;(4)以点P为圆心,为半径的圆有无数个.
A.1个
B.2个
C.3个
D.4个
解:①经过P点的圆有无数个,故①正确;
②以点P为圆心的圆有无数个,半径不确定,故②正确;
③半径为3cm,且经过点P的圆有无数个,圆心不确定有无数个,故③正确;
④以点P为圆心,以3cm为半径的圆有一个,故④错误.故选:A.
针对性训练
如图所示,BD,CE是△ABC的高.
求证:E,B,C,D四点在同一个圆上.
,,试求过E,B,C,D四点的圆的半径.
(1)证明:取BC的中点O,连接OD,OE.
∵BD,CE是△ABC的高,∴△BCD和△BCE都是直角三角形.
∴OD,OE分别为Rt△BCD和Rt△BCE斜边上的中线,
∴OD=OE=OB=OC.
∴B、C、D、E四点在以O点为圆心,12BC为半径的圆上.
(2)解:∵∠BEC=90°,∴BC是圆的直径,∵∠ABC=60°,CE=12,
∴BC=,(运用三角函数或者30°60°90°三角形对边之比1::2)
∴圆的半径为.
知识点2
圆的有关概念(重点;理解)
【命题点2
圆有关的概念】
例2
以下命题:
(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧;(7)以O为圆心可以画无数个圆.正确的个数为
(
)
A.1个
B.2个
C.3个
D.4个
知识点3
圆的对称性
(了解)
【命题点3
圆的对称性】
例3
下列图形中,对称轴条数最多的是(
)
线段
B.正方形
C.正三角形
D.圆
知识点4
垂径定理及其推论(重点、难点;理解)
【命题点4
利用垂径定理解决实际问题】
例4
AB是⊙O的直径,CD是弦,与点E,则下列结论中不一定成立的是(
)
A.
B.
C.
D.︵BD=︵BC
针对性训练
1.把球放在长方体纸盒内,球的一部分露在盒外,其截面如图所示,已知圆心为O,,则⊙O的半径为多少厘米?
解:过点O作OM⊥AD于点M,连接OF,
设OF=x,则OM=16?x,MF=8,
在直角三角形OMF中,OM+MF=OF
即:(16?x)+8=x,解得:x=10
答:⊙O的半径为10厘米.
2.已知:如图,⊙O的直径AB和CD相交于点E.已知AE=1㎝,EB=5㎝,∠DEB=600,求CD的长.
作OH⊥CD于H,连接OD,
∵AE=1cm,BE=5cm,E在直径AB上,
∴AB=1cm+5cm=6cm,半径OD=3cm,
∵在Rt△OHE中,OE=3cm?1cm=2cm,∠OEH=60°,∴OH=cm,
在Rt△OHD中,由勾股定理得:HD=cm,
∵OH⊥CD,∴由垂径定理得:DC=2DH=cm;
知识点5
弧、弦、圆心角之间的关系(重点;理解)
【命题点5
根据圆心角、弧、弦之间关系求角的度数】
例5
如图所示,AB是⊙O的直径,==,,则的度数是
(
)
A.51°
B.56°
C.68°
D.78°
针对性训练
如图所示,四边形ABCD的四个顶点都在⊙O上,于E,于F,求证:.
分析:如图,作辅助线;证明∠DBC=∠BAG,得到BG=DC;证明OF是△ABG的中位线,得到BG=2OF,即可解决问题.
证明:如图,连接AO并延长,交⊙O于点G;则∠ABG=90°;而AC⊥BD,
∴∠DBC=90°?∠ACB,∠BAG=90°?∠AGB,
∵∠ACB=∠AGB,∴∠DBC=∠BAG,∴BG=DC;
∵OF⊥AB,∠ABG=90°,∴OF∥BG,AF=BF;而OA=OG,
∴OF是△ABG的中位线,∴BG=2OF,∴2OF=CD.
知识点6
圆周角的定义和圆周角定理
(重点、难点;理解)
【命题点6
应用圆周角定理求角的度数】
例6
如图所示,A、B、C是⊙O上的三点,,则=
60
度.
针对性训练
如图所示,若AB是⊙O的直径,CD是⊙O的弦,,则等于
(
)
A.116°
B.32°
C.58°
D.64°
知识点7
圆内接多边形的概念及圆内接四边形的性质(重点;理解)
【命题点7
圆内接四边形的应用】
例7
如图所示,在圆内接四边形ABCD中,,则
.
二、全方位技巧
类型题1
圆的定义和四边形的综合
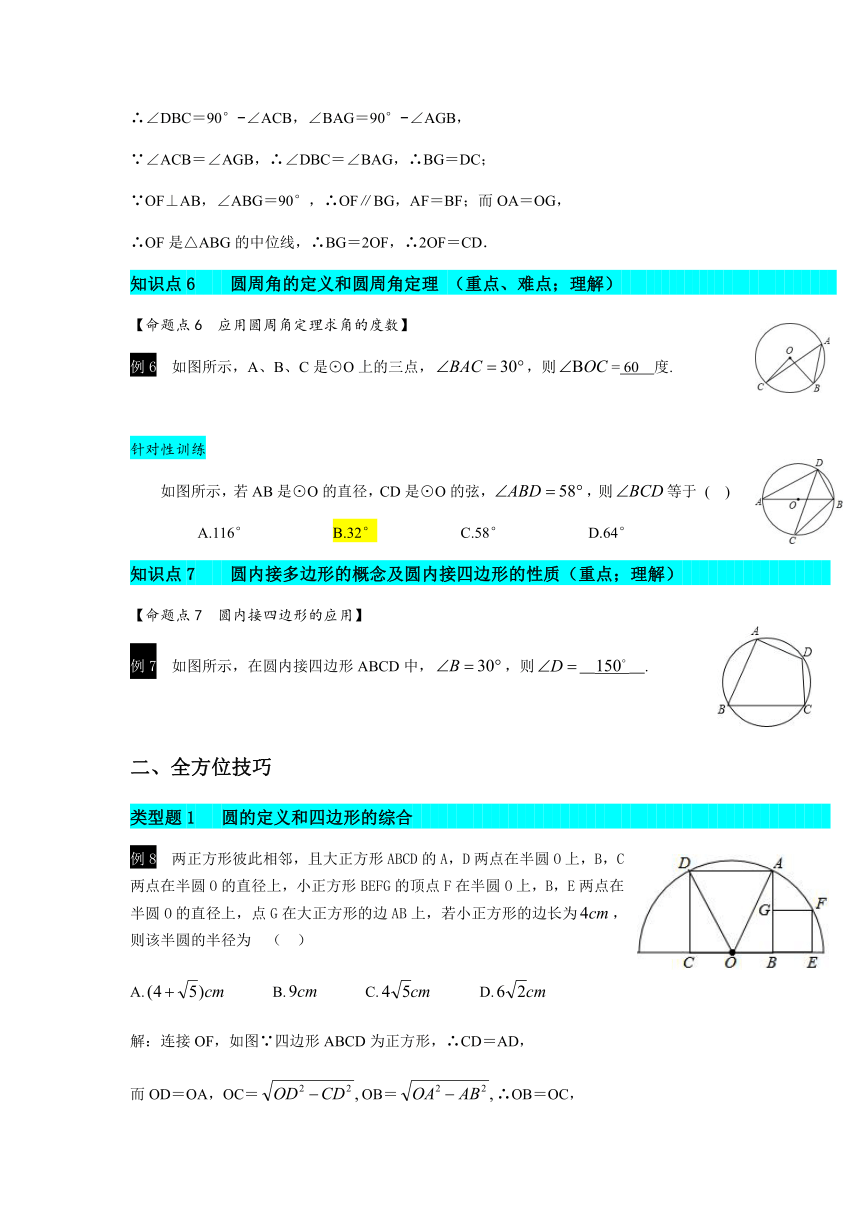
例8
两正方形彼此相邻,且大正方形ABCD的A,D两点在半圆O上,B,C两点在半圆O的直径上,小正方形BEFG的顶点F在半圆O上,B,E两点在半圆O的直径上,点G在大正方形的边AB上,若小正方形的边长为,则该半圆的半径为
(
)
B.
C.
D.
解:连接OF,如图∵四边形ABCD为正方形,∴CD=AD,
而OD=OA,OC=OB=∴OB=OC,
设OB=x,则OE=x+4,AB=2x,
在Rt△AOB中,OA=OB+AB=x+(2x)=5x,
在Rt△OEF中有OF=OE+EF=(x+4)+4,
而OA=OF,∴(x+4)+4=5x,整理得x?2x?8=0,解得=4,=?2(舍去),∴OA=,即该圆的半径为.
类型题2
圆在实际问题中的应用
例9
如图示,某部队在灯塔A的周围进行爆破作业,已知灯塔A的周围内的水域为危险区域,有一渔船误入与灯塔A的距离为的B处,为了尽快驶离危险区域,该渔船应沿哪条射线的方向航行?说明理由.
类型题3
垂径定理与平面直角坐标系的综合应用
例10
如图示,在平面直角坐标系中,点O为坐标原点,点P在第一象限,
⊙P与轴交于O、A两点,点A的坐标为,⊙P的半径为,则点P的坐标为
.
解:过点P作PD⊥x轴于点D,连接OP,
∵A(6,0),PD⊥OA,∴OD=OA=3,
在Rt△OPD中,∵OP=,OD=3,∴PD=,∴P(3,2).
类型题4
利用“分类讨论”解圆中的计算问题
例11
已知AB,CD为⊙O的两条平行弦,⊙O半径为,,,求弦AB,CD间的距离.
解:如图所示,连接OA,OC.作直线EF⊥AB于E,交CD于F,则EF⊥CD.
∵OE⊥AB,OF⊥CD,
∴AE=AB=3,CF=CD=4.
根据勾股定理,得OE=4,OF=3.
①当AB和CD在圆心的同侧时,则EF=OE?OF=1(cm);
②当AB和CD在圆心的两侧时,则EF=OE+OF=7(cm).
则AB与CD间的距离为1cm或7cm.
类型题5
圆周角定理的推论与垂径定理的综合应用
例12
如图所示,点C,D在以AB为直径的⊙O上,且CD平分,若,,则CD的长为
.
解:连接OC,过点O作OE⊥CD,垂足为点E,
∵∠CAB=15°,OC=OA,∴∠OCA=15°,
∵AB是⊙O的直径,∴∠ACB=90°,
∵CD平分∠ACB,∴∠ACD=45°,∴∠OCE=∠ACD?∠OCA=45°?15°=30°,
∵AB=2OC=2,∴OC=1,∴OE=OC=,∴CE=
∴CD=2CE=.
类型题6
巧引辅助线,构造特殊三角形解题
例13
如图所示,在⊙O中,,.
求的度数.
求⊙O的周长.
解:(1)∠BAC=∠BDC=60°(同弧所对的圆周角相等);
(2)∠ABC=180°?∠BAC?∠ACB=60°,
∴△ABC是等边三角形,
作OE⊥AC于点E,连接OA,则OA平分∠BAC,
∴∠OAE=30°,∴OA=
所以⊙O的周长=2π×2=4πcm.
类型题7
利用“分类讨论”解圆中的计算问题
例14
几何模型:
条件:如图所示,A,B是直线同旁的两个定点.
问题:在直线上确定一点P,使的值最小.
方法:作点A关于直线的对称点,连接交于点P,则的值最小.
模型应用:
正方形ABCD的边长为2,E为AB的中点,P是AC上一动点,连接BD,由正方形对称性可知,B与D关于直线AC对称,连接ED交AC与P,则PB+PC的最小值是
;
⊙O的半径为2,点A,B,C在⊙O上,,,P是OB上一动点,求的最小值;
AB,CD是半径为5的⊙O的两条弦,,MN是直径,于点E,于点F,P为EF上的任意一点,求的最小值.
三、分层实战训练
【基础巩固】
1.如下列命题中正确的有(
)
①直径是圆内最长的弦;②弦是半圆;③过圆心的直线是直径;④半圆是圆弧.
A.1个
B.2个
C.3个
D.4个
下列命题中,正确的是(
)
过弦的中点的直线平分弦所对的弧
B.过弦的中点的直线必过圆心
C.弦所对的两条弧的中点连线垂直平分弦且过圆心
D.弦的垂线平分弦所对的弧
3.
如图所示,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D.求证:AB=CD.
析:过O作OM⊥AB于M,ON⊥CD于N,连接OA、OC,根据角平分线性质得出ON=OM,根据勾股定理求出AM=CN,根据垂径定理得出AB=2AM,CD=2CN,即可得出答案.
⊙O1,⊙O2相交于A、B两点,两圆半径分别为和,两圆的连心线O1O2的长为,则弦AB的长为(
)
已知P是⊙O内一点,⊙O的半径为15,P点到圆心O的距离是9,则经过P点且长度是整数的弦的条数是(
)
6.在同圆中,如果=2,那么弦AB与弦CD的关系为AB
<
2CD.
7.已知⊙O中弦AB的长等于半径长,求弦AB所对的圆心角和圆周角的度数.
解:连接OA、OB,∵AB=OA=OB,∴∠AOB=60°.
分两种情况:
①在优弧上任取一点C,连接CA,CB,
则∠C=∠AOB=30°,
②在劣弧上任取一点D,连接AD、BD,
∵四边形ADBC是⊙O的内接四边形,
∴∠C+∠ADB=180°,
∴∠ADB=180°?∠C=150°.
综上所述,弦AB所对的圆心角是60°,圆周角是30°或150°.
【能力提升】
8.如图所示,MN是半径为1的⊙O的直径,点A在⊙O上,,
B为的中点,点P是直径MN上的一个动点,则的最小值为(
)
A.
B.
C.
D.
解:过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,连接OB,OA′,AA′,
∵AA′关于直线MN对称,∴=,
∵∠AMN=30°,∴∠A′ON=60°,∠BON=30°,∴∠A′OB=90°,
在Rt△A′OB中,OB=OA′=1,∴A′B=,即PA+PB的最小值.
故选:B.
9.如图所示,等边三角形ABC的顶点都在⊙O上,P是AB上任一点(点P不与点A,B重合),连接AP,BP,CP,过点C作CM∥BP交PA的延长线于点M.
(1)
度,
度;
(2)求证△ACM≌△BCP;
(3)若,,求梯形PBCM的面积.
【中考链接】
10.如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且,.
(1)求的度数;
(2)过点O作于点F,延长FO交BE与点G,,,求AB的长.
圆的有关性质
一、知识点过关
知识点1
圆的定义及其表示方法
(重点;理解)
【命题点1
圆的定义】
例1
下列说法中,错误的有
(
)
(1)经过点P的圆有无数个;
(2)以点P为圆心的圆有无数个;
(3)半径为且经过点P的圆有无数个;(4)以点P为圆心,为半径的圆有无数个.
A.1个
B.2个
C.3个
D.4个
解:①经过P点的圆有无数个,故①正确;
②以点P为圆心的圆有无数个,半径不确定,故②正确;
③半径为3cm,且经过点P的圆有无数个,圆心不确定有无数个,故③正确;
④以点P为圆心,以3cm为半径的圆有一个,故④错误.故选:A.
针对性训练
如图所示,BD,CE是△ABC的高.
求证:E,B,C,D四点在同一个圆上.
,,试求过E,B,C,D四点的圆的半径.
(1)证明:取BC的中点O,连接OD,OE.
∵BD,CE是△ABC的高,∴△BCD和△BCE都是直角三角形.
∴OD,OE分别为Rt△BCD和Rt△BCE斜边上的中线,
∴OD=OE=OB=OC.
∴B、C、D、E四点在以O点为圆心,12BC为半径的圆上.
(2)解:∵∠BEC=90°,∴BC是圆的直径,∵∠ABC=60°,CE=12,
∴BC=,(运用三角函数或者30°60°90°三角形对边之比1::2)
∴圆的半径为.
知识点2
圆的有关概念(重点;理解)
【命题点2
圆有关的概念】
例2
以下命题:
(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧;(7)以O为圆心可以画无数个圆.正确的个数为
(
)
A.1个
B.2个
C.3个
D.4个
知识点3
圆的对称性
(了解)
【命题点3
圆的对称性】
例3
下列图形中,对称轴条数最多的是(
)
线段
B.正方形
C.正三角形
D.圆
知识点4
垂径定理及其推论(重点、难点;理解)
【命题点4
利用垂径定理解决实际问题】
例4
AB是⊙O的直径,CD是弦,与点E,则下列结论中不一定成立的是(
)
A.
B.
C.
D.︵BD=︵BC
针对性训练
1.把球放在长方体纸盒内,球的一部分露在盒外,其截面如图所示,已知圆心为O,,则⊙O的半径为多少厘米?
解:过点O作OM⊥AD于点M,连接OF,
设OF=x,则OM=16?x,MF=8,
在直角三角形OMF中,OM+MF=OF
即:(16?x)+8=x,解得:x=10
答:⊙O的半径为10厘米.
2.已知:如图,⊙O的直径AB和CD相交于点E.已知AE=1㎝,EB=5㎝,∠DEB=600,求CD的长.
作OH⊥CD于H,连接OD,
∵AE=1cm,BE=5cm,E在直径AB上,
∴AB=1cm+5cm=6cm,半径OD=3cm,
∵在Rt△OHE中,OE=3cm?1cm=2cm,∠OEH=60°,∴OH=cm,
在Rt△OHD中,由勾股定理得:HD=cm,
∵OH⊥CD,∴由垂径定理得:DC=2DH=cm;
知识点5
弧、弦、圆心角之间的关系(重点;理解)
【命题点5
根据圆心角、弧、弦之间关系求角的度数】
例5
如图所示,AB是⊙O的直径,==,,则的度数是
(
)
A.51°
B.56°
C.68°
D.78°
针对性训练
如图所示,四边形ABCD的四个顶点都在⊙O上,于E,于F,求证:.
分析:如图,作辅助线;证明∠DBC=∠BAG,得到BG=DC;证明OF是△ABG的中位线,得到BG=2OF,即可解决问题.
证明:如图,连接AO并延长,交⊙O于点G;则∠ABG=90°;而AC⊥BD,
∴∠DBC=90°?∠ACB,∠BAG=90°?∠AGB,
∵∠ACB=∠AGB,∴∠DBC=∠BAG,∴BG=DC;
∵OF⊥AB,∠ABG=90°,∴OF∥BG,AF=BF;而OA=OG,
∴OF是△ABG的中位线,∴BG=2OF,∴2OF=CD.
知识点6
圆周角的定义和圆周角定理
(重点、难点;理解)
【命题点6
应用圆周角定理求角的度数】
例6
如图所示,A、B、C是⊙O上的三点,,则=
60
度.
针对性训练
如图所示,若AB是⊙O的直径,CD是⊙O的弦,,则等于
(
)
A.116°
B.32°
C.58°
D.64°
知识点7
圆内接多边形的概念及圆内接四边形的性质(重点;理解)
【命题点7
圆内接四边形的应用】
例7
如图所示,在圆内接四边形ABCD中,,则
.
二、全方位技巧
类型题1
圆的定义和四边形的综合
例8
两正方形彼此相邻,且大正方形ABCD的A,D两点在半圆O上,B,C两点在半圆O的直径上,小正方形BEFG的顶点F在半圆O上,B,E两点在半圆O的直径上,点G在大正方形的边AB上,若小正方形的边长为,则该半圆的半径为
(
)
B.
C.
D.
解:连接OF,如图∵四边形ABCD为正方形,∴CD=AD,
而OD=OA,OC=OB=∴OB=OC,
设OB=x,则OE=x+4,AB=2x,
在Rt△AOB中,OA=OB+AB=x+(2x)=5x,
在Rt△OEF中有OF=OE+EF=(x+4)+4,
而OA=OF,∴(x+4)+4=5x,整理得x?2x?8=0,解得=4,=?2(舍去),∴OA=,即该圆的半径为.
类型题2
圆在实际问题中的应用
例9
如图示,某部队在灯塔A的周围进行爆破作业,已知灯塔A的周围内的水域为危险区域,有一渔船误入与灯塔A的距离为的B处,为了尽快驶离危险区域,该渔船应沿哪条射线的方向航行?说明理由.
类型题3
垂径定理与平面直角坐标系的综合应用
例10
如图示,在平面直角坐标系中,点O为坐标原点,点P在第一象限,
⊙P与轴交于O、A两点,点A的坐标为,⊙P的半径为,则点P的坐标为
.
解:过点P作PD⊥x轴于点D,连接OP,
∵A(6,0),PD⊥OA,∴OD=OA=3,
在Rt△OPD中,∵OP=,OD=3,∴PD=,∴P(3,2).
类型题4
利用“分类讨论”解圆中的计算问题
例11
已知AB,CD为⊙O的两条平行弦,⊙O半径为,,,求弦AB,CD间的距离.
解:如图所示,连接OA,OC.作直线EF⊥AB于E,交CD于F,则EF⊥CD.
∵OE⊥AB,OF⊥CD,
∴AE=AB=3,CF=CD=4.
根据勾股定理,得OE=4,OF=3.
①当AB和CD在圆心的同侧时,则EF=OE?OF=1(cm);
②当AB和CD在圆心的两侧时,则EF=OE+OF=7(cm).
则AB与CD间的距离为1cm或7cm.
类型题5
圆周角定理的推论与垂径定理的综合应用
例12
如图所示,点C,D在以AB为直径的⊙O上,且CD平分,若,,则CD的长为
.
解:连接OC,过点O作OE⊥CD,垂足为点E,
∵∠CAB=15°,OC=OA,∴∠OCA=15°,
∵AB是⊙O的直径,∴∠ACB=90°,
∵CD平分∠ACB,∴∠ACD=45°,∴∠OCE=∠ACD?∠OCA=45°?15°=30°,
∵AB=2OC=2,∴OC=1,∴OE=OC=,∴CE=
∴CD=2CE=.
类型题6
巧引辅助线,构造特殊三角形解题
例13
如图所示,在⊙O中,,.
求的度数.
求⊙O的周长.
解:(1)∠BAC=∠BDC=60°(同弧所对的圆周角相等);
(2)∠ABC=180°?∠BAC?∠ACB=60°,
∴△ABC是等边三角形,
作OE⊥AC于点E,连接OA,则OA平分∠BAC,
∴∠OAE=30°,∴OA=
所以⊙O的周长=2π×2=4πcm.
类型题7
利用“分类讨论”解圆中的计算问题
例14
几何模型:
条件:如图所示,A,B是直线同旁的两个定点.
问题:在直线上确定一点P,使的值最小.
方法:作点A关于直线的对称点,连接交于点P,则的值最小.
模型应用:
正方形ABCD的边长为2,E为AB的中点,P是AC上一动点,连接BD,由正方形对称性可知,B与D关于直线AC对称,连接ED交AC与P,则PB+PC的最小值是
;
⊙O的半径为2,点A,B,C在⊙O上,,,P是OB上一动点,求的最小值;
AB,CD是半径为5的⊙O的两条弦,,MN是直径,于点E,于点F,P为EF上的任意一点,求的最小值.
三、分层实战训练
【基础巩固】
1.如下列命题中正确的有(
)
①直径是圆内最长的弦;②弦是半圆;③过圆心的直线是直径;④半圆是圆弧.
A.1个
B.2个
C.3个
D.4个
下列命题中,正确的是(
)
过弦的中点的直线平分弦所对的弧
B.过弦的中点的直线必过圆心
C.弦所对的两条弧的中点连线垂直平分弦且过圆心
D.弦的垂线平分弦所对的弧
3.
如图所示,点O是∠EPF的平分线上的一点,以O为圆心的圆和角的两边分别交于点A、B和C、D.求证:AB=CD.
析:过O作OM⊥AB于M,ON⊥CD于N,连接OA、OC,根据角平分线性质得出ON=OM,根据勾股定理求出AM=CN,根据垂径定理得出AB=2AM,CD=2CN,即可得出答案.
⊙O1,⊙O2相交于A、B两点,两圆半径分别为和,两圆的连心线O1O2的长为,则弦AB的长为(
)
已知P是⊙O内一点,⊙O的半径为15,P点到圆心O的距离是9,则经过P点且长度是整数的弦的条数是(
)
6.在同圆中,如果=2,那么弦AB与弦CD的关系为AB
<
2CD.
7.已知⊙O中弦AB的长等于半径长,求弦AB所对的圆心角和圆周角的度数.
解:连接OA、OB,∵AB=OA=OB,∴∠AOB=60°.
分两种情况:
①在优弧上任取一点C,连接CA,CB,
则∠C=∠AOB=30°,
②在劣弧上任取一点D,连接AD、BD,
∵四边形ADBC是⊙O的内接四边形,
∴∠C+∠ADB=180°,
∴∠ADB=180°?∠C=150°.
综上所述,弦AB所对的圆心角是60°,圆周角是30°或150°.
【能力提升】
8.如图所示,MN是半径为1的⊙O的直径,点A在⊙O上,,
B为的中点,点P是直径MN上的一个动点,则的最小值为(
)
A.
B.
C.
D.
解:过A作关于直线MN的对称点A′,连接A′B,由轴对称的性质可知A′B即为PA+PB的最小值,连接OB,OA′,AA′,
∵AA′关于直线MN对称,∴=,
∵∠AMN=30°,∴∠A′ON=60°,∠BON=30°,∴∠A′OB=90°,
在Rt△A′OB中,OB=OA′=1,∴A′B=,即PA+PB的最小值.
故选:B.
9.如图所示,等边三角形ABC的顶点都在⊙O上,P是AB上任一点(点P不与点A,B重合),连接AP,BP,CP,过点C作CM∥BP交PA的延长线于点M.
(1)
度,
度;
(2)求证△ACM≌△BCP;
(3)若,,求梯形PBCM的面积.
【中考链接】
10.如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且,.
(1)求的度数;
(2)过点O作于点F,延长FO交BE与点G,,,求AB的长.
同课章节目录
