人教版八年级数学13.1.2 线段的垂直平分线(共16张ppt)
文档属性
| 名称 | 人教版八年级数学13.1.2 线段的垂直平分线(共16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 12:28:50 | ||
图片预览




文档简介
(共16张PPT)
13.1.2
线段的垂直平分线
知识点复习
线段的垂直平分线的定义:
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
课堂目标
1、识记线段垂直平分线的性质定理和判定定理。
2、会应用线段垂直平分线的性质定理和判定定理解决相关问题。
命题:线段垂直平分线上的点和这条线段两个端点的距离相等。
由此你能得到什么规律?
线段垂直平分线的性质定理
如图,作线段AB的垂直平分线
,垂足为点0。
(1)在直线
上任取一点P1,连接P1A、P1B,试探究P1A与P1B之间的数量关系。
(2)在直线
上任取一点P2,连接P2A、P2B,试探究P2A与P2B之间的数量关系。
P1A
=
P1B
P2A
=
P2B
P3A
=
P3B
……
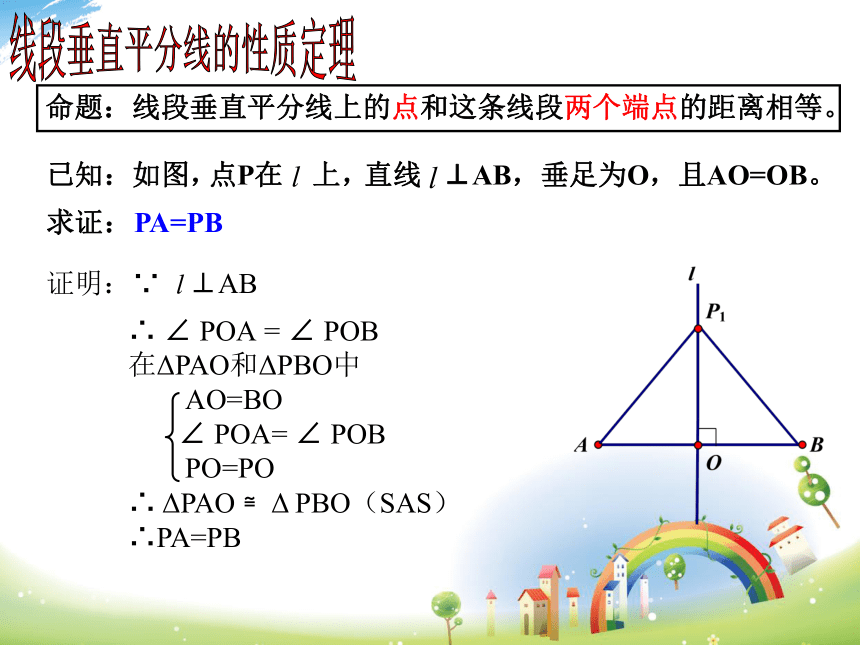
命题:线段垂直平分线上的点和这条线段两个端点的距离相等。
PA=PB
已知:如图,
求证:
线段垂直平分线的性质定理
直线
⊥AB,垂足为O,且AO=OB。
∴
∠
POA
=
∠
POB
在ΔPAO和ΔPBO中
AO=BO
∠
POA=
∠
POB
PO=PO
∴
ΔPAO
≌Δ
PBO(SAS)
∴PA=PB
证明:∵
⊥AB
点P在
上,
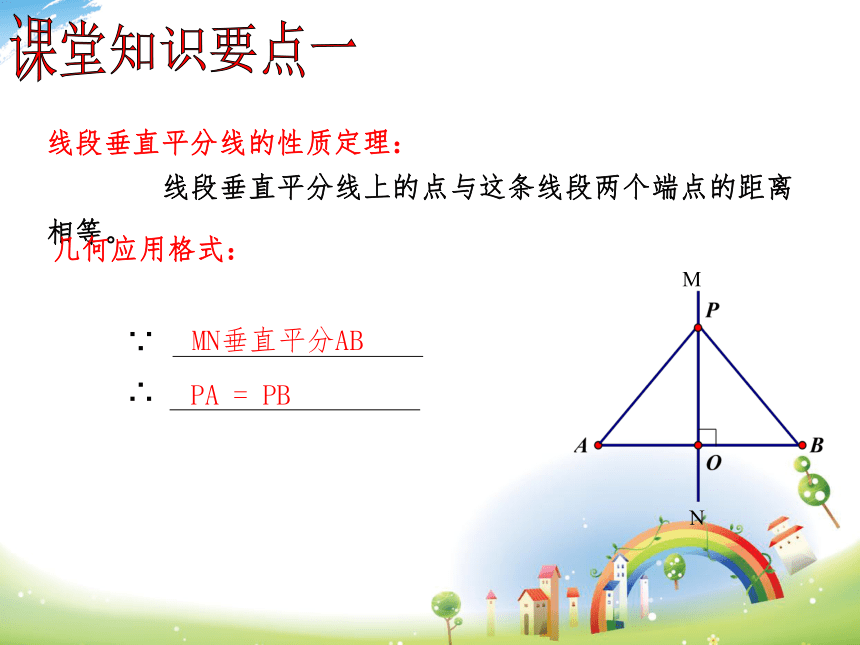
线段垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等。
课堂知识要点一
几何应用格式:
∵
∴
M
N
MN垂直平分AB
PA
=
PB
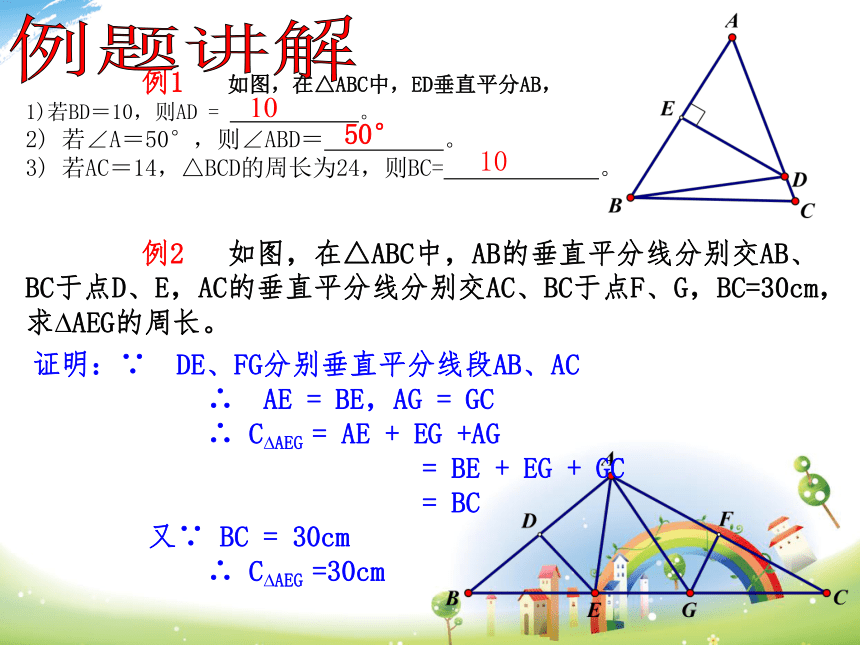
例1
如图,在△ABC中,ED垂直平分AB,
1)若BD=10,则AD
=
。
2)
若∠A=50°,则∠ABD=
。
3)
若AC=14,△BCD的周长为24,则BC=
。
例题讲解
10
例2
如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,BC=30cm,求?AEG的周长。
证明:∵
DE、FG分别垂直平分线段AB、AC
∴
AE
=
BE,AG
=
GC
∴
C?AEG
=
AE
+
EG
+AG
=
BE
+
EG
+
GC
=
BC
又∵
BC
=
30cm
∴
C?AEG
=30cm
50°
10
(4分)如图,点A,B,C表示某公司三个车间的位置,现要建一个仓库,要求它到三个车间的距离相等,则仓库应建在△ABC
的交点上.
三边垂直平分线
反过来:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上吗?
已知:如图,MA=MB
求证:点M在AB的垂直平分线上。
线段垂直平分线的判定定理
线段垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等。
已知:如图,MA=MB
求证:点M在AB的垂直平分线上。
线段垂直平分线的判定定理
证明:过点M作直线MO,使MO⊥AB于点O
则:∠AOM
=
∠BOM
=
90°
在Rt?AOM和Rt?BOM中
AM
=
BM
OM
=
OM
∴
Rt?AOM≌Rt?BOM(HL)
∴
AO
=
BO
即:点M在AB的垂直平分线上
课堂知识要点二
线段垂直平分线的判定定理:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
几何应用格式:
∵
∴
MA
=
MB
点M在线段AB的垂直平分线上
错误应用格式:
∵
∴
MA
=
MB
MO垂直平分AB
线段的垂直平分线可以
看作和线段两个端点距离相
等的所有点的集合。
例题讲解
例
如图,在?ABC中,OE垂直平分AB,且OA=OC。
求证:点O在BC的垂直平分线上。
证明:连接OB
∵
OE是AB的垂直平分线
∴
OA
=
OB
又∵
OA
=
OC
∴
OB
=
OC
∴
点O在BC的垂直平分线上
课堂知识要点
线段垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等。
几何应用格式:
∵
∴
M
N
MN垂直平分AB
PA
=
PB
线段垂直平分线的判定定理:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
几何应用格式:
∵
∴
MA
=
MB
点M在线段AB的垂直平分线
(4分)如图,在△ABC中,AB=5
cm,AC=3
cm,BC的垂直平分线分别交AB,BC于点D,E,则△ACD的周长为
cm.
8
(6分)如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上.若AB=5
cm,BD=3
cm,求BE的长.
(4分)如图,在△ABC中,D为BC上一点,且BC=BD+AD,则点D在线段
的垂直平分线上.
AC
13.1.2
线段的垂直平分线
知识点复习
线段的垂直平分线的定义:
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线。
课堂目标
1、识记线段垂直平分线的性质定理和判定定理。
2、会应用线段垂直平分线的性质定理和判定定理解决相关问题。
命题:线段垂直平分线上的点和这条线段两个端点的距离相等。
由此你能得到什么规律?
线段垂直平分线的性质定理
如图,作线段AB的垂直平分线
,垂足为点0。
(1)在直线
上任取一点P1,连接P1A、P1B,试探究P1A与P1B之间的数量关系。
(2)在直线
上任取一点P2,连接P2A、P2B,试探究P2A与P2B之间的数量关系。
P1A
=
P1B
P2A
=
P2B
P3A
=
P3B
……
命题:线段垂直平分线上的点和这条线段两个端点的距离相等。
PA=PB
已知:如图,
求证:
线段垂直平分线的性质定理
直线
⊥AB,垂足为O,且AO=OB。
∴
∠
POA
=
∠
POB
在ΔPAO和ΔPBO中
AO=BO
∠
POA=
∠
POB
PO=PO
∴
ΔPAO
≌Δ
PBO(SAS)
∴PA=PB
证明:∵
⊥AB
点P在
上,
线段垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等。
课堂知识要点一
几何应用格式:
∵
∴
M
N
MN垂直平分AB
PA
=
PB
例1
如图,在△ABC中,ED垂直平分AB,
1)若BD=10,则AD
=
。
2)
若∠A=50°,则∠ABD=
。
3)
若AC=14,△BCD的周长为24,则BC=
。
例题讲解
10
例2
如图,在△ABC中,AB的垂直平分线分别交AB、BC于点D、E,AC的垂直平分线分别交AC、BC于点F、G,BC=30cm,求?AEG的周长。
证明:∵
DE、FG分别垂直平分线段AB、AC
∴
AE
=
BE,AG
=
GC
∴
C?AEG
=
AE
+
EG
+AG
=
BE
+
EG
+
GC
=
BC
又∵
BC
=
30cm
∴
C?AEG
=30cm
50°
10
(4分)如图,点A,B,C表示某公司三个车间的位置,现要建一个仓库,要求它到三个车间的距离相等,则仓库应建在△ABC
的交点上.
三边垂直平分线
反过来:
到一条线段两个端点距离相等的点,在这条线段的垂直平分线上吗?
已知:如图,MA=MB
求证:点M在AB的垂直平分线上。
线段垂直平分线的判定定理
线段垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等。
已知:如图,MA=MB
求证:点M在AB的垂直平分线上。
线段垂直平分线的判定定理
证明:过点M作直线MO,使MO⊥AB于点O
则:∠AOM
=
∠BOM
=
90°
在Rt?AOM和Rt?BOM中
AM
=
BM
OM
=
OM
∴
Rt?AOM≌Rt?BOM(HL)
∴
AO
=
BO
即:点M在AB的垂直平分线上
课堂知识要点二
线段垂直平分线的判定定理:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
几何应用格式:
∵
∴
MA
=
MB
点M在线段AB的垂直平分线上
错误应用格式:
∵
∴
MA
=
MB
MO垂直平分AB
线段的垂直平分线可以
看作和线段两个端点距离相
等的所有点的集合。
例题讲解
例
如图,在?ABC中,OE垂直平分AB,且OA=OC。
求证:点O在BC的垂直平分线上。
证明:连接OB
∵
OE是AB的垂直平分线
∴
OA
=
OB
又∵
OA
=
OC
∴
OB
=
OC
∴
点O在BC的垂直平分线上
课堂知识要点
线段垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等。
几何应用格式:
∵
∴
M
N
MN垂直平分AB
PA
=
PB
线段垂直平分线的判定定理:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
几何应用格式:
∵
∴
MA
=
MB
点M在线段AB的垂直平分线
(4分)如图,在△ABC中,AB=5
cm,AC=3
cm,BC的垂直平分线分别交AB,BC于点D,E,则△ACD的周长为
cm.
8
(6分)如图,AD⊥BC,BD=CD,点C在AE的垂直平分线上.若AB=5
cm,BD=3
cm,求BE的长.
(4分)如图,在△ABC中,D为BC上一点,且BC=BD+AD,则点D在线段
的垂直平分线上.
AC
