人教版七年级数学上册 3.4 一元一次方程应用(工程问题)(共28张ppt)
文档属性
| 名称 | 人教版七年级数学上册 3.4 一元一次方程应用(工程问题)(共28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 543.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 12:49:44 | ||
图片预览








文档简介
(共28张PPT)
第三章 一元一次方程
工程问题
复习:
工作量、工作时间、工作效率的关系:
(1)工作量=___________
×
____________;
(2)工作时间=___________÷____________;
(3)工作效率=___________÷____________;
工作时间
工作效率
工作量
工作效率
工作量
工作时间
知识复习
问题1.小学我们学过工程问题,请回答下列问题.
(1)一项工作甲单独做需要5天完成,乙单独做需要10天完成,那么甲每天的工作效率是____,乙每天的工作效率是____,两人合作3天完成的工作量是_________,此时剩余的工作量是_____.
复习提问
(2)一项工作甲单独做需要a天完成,乙单独做需要b天完成,那么甲每天的工作效率是____,乙每天的工作效率是____,两人合作3天完成的工作量是_________,此时剩余的工作量是_________.
复习提问
问题1.小学我们学过工程问题,请回答下列问题.
归纳小结:
为简便起见,通常设总工作量为“1”.
1.如果已知工作时间,
那么“时间的倒数”就是工作效率.
知识归纳
2.如果工程为多方合作完成,
则合作完成时的工作效率是各方的工作效率相加.
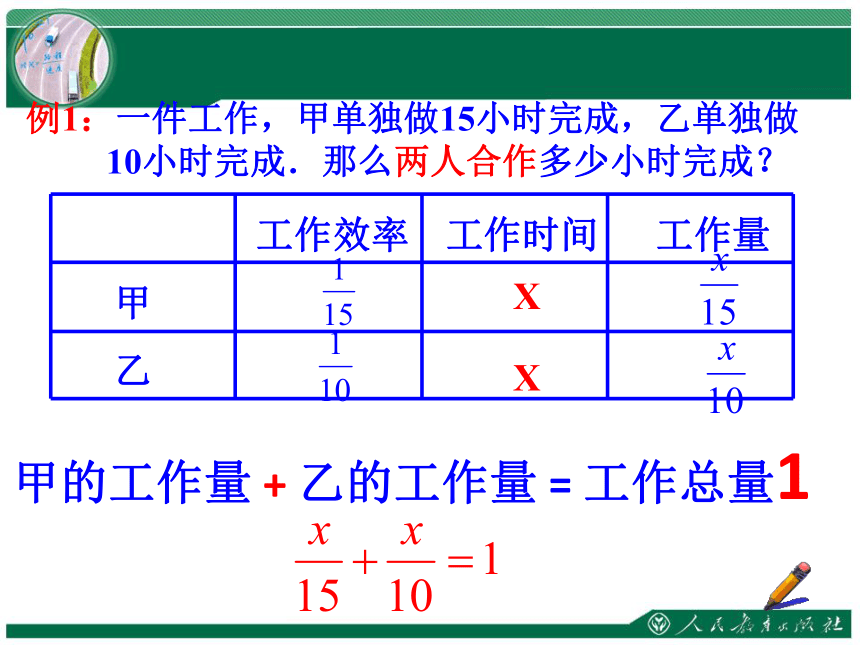
例1:一件工作,甲单独做15小时完成,乙单独做
10小时完成.那么两人合作多少小时完成?
甲
乙
工作效率
工作时间
工作量
X
X
甲的工作量
+
乙的工作量
=
工作总量1
甲的工作量
+
乙的工作量
=
工作总量1
解:设两人合作x小时完成此工作,
依题意,得:
答:两人合作6小时完成.?
去分母,得
4x+6x=60
合并同类项,得
10x=60
系数化为1,得
x=6
变式1:一件工作,甲单独做15小时完成,乙单独做10
小时完成.甲先单独做9小时,后因甲有其它任务
调离,余下的任务由乙单独完成。那么乙还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
9
X
甲的工作量
+
乙的工作量
=
工作总量1
答:乙还要4小时完成.
解:设乙还需x小时完成此工作,依题意,得:
解得
x=4
变式2:一件工作,甲单独做15小时完成,乙单独做
12小时完成.甲先单独做6小时,然后乙加入
合作,那么两人合作还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
X+6
X
甲的工作量
+
乙的工作量
=
工作总量1
甲的工作量
+
乙的工作量
=
工作总量1
答:两人合作还要4小时完成.
解:设两人合作还需x小时完成此工作,
依题意,得:
解得
x=4
变式3:一件工作,甲单独做15小时完成,甲、乙合做
6小时完成.甲先单独做6小时,余下的乙单独做,那么乙还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
6
X
甲的工作量
+
乙的工作量
=
工作总量1
答:乙还要6小时完成.
解:设乙还需x小时完成此工作,依题意,得:
解得
x=6
列表分析:
问题探究
例2:整理一批图书,由一个人做要40h完成.现计划由一部分人先做4
h,然后增加
2人与他们一起做8
h,完成这项工作.
假设这些人的工作效率相同,具体应该先安排多少人工作?
列表分析:
人均效率
人数
时间
工作量
前一部分工作
后一部分工作
×
=
×
×
×
=
问题探究
(x+2)
x
4
8
解:设安排
x
人先做4
h.
依题意得,
.
解方程得
,
4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应安排
2人先做4
h.
问题探究
例3:某工厂接受了加工一批零件的任务,按原来每天的定额,预计30天可以完成。由于进行了技术革新,工作效率比原来提高了50%,结果提前8天完成任务,并且多加工了24件,原来接受的加工任务是多少?原来每天加工的定额是多少?
原来
实际
工作效率
工作时间
工作量
30
30-8
1.一条地下管线由甲工程队单独铺设需要
12天完成,由乙工程队单独铺设需要24天完成.
如果由这两个工程队从两端同时施工,需要多少天才能完成这条管线的铺设任务?
解:设两个工程队合作施工,
x天可以铺好这条管线.
依题意,得
解方程,得
x=8.
答:两个工程队从两端同时施工,需要8天才能完成这条管线的铺设任务.
巩固练习
2.收割一块水稻田,若每小时收割4亩,预计若干小时完成,收割
后,改用新式农机,工作效率提高到原来的
倍,因此比预计时间提早1小时完成.求这块水稻田的面积.
巩固练习
解:设这块水稻田的面积为x亩.
依题意,得
.
解方程,得
x=36.
答:这块水稻田的面积为36亩.
巩固练习
用一元一次方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x
=
a)
实际问题的答案
检
验
探究
课堂小结
1.本节课学习的主要内容是什么?
2.分析实际问题中的数量关系,常用的方法是什么?需要注意哪些问题?
3.通过本节课的学习,尝试用自己的语言描述,如何建立方程模型来解决实际问题?
第三章 一元一次方程
工程问题
复习:
工作量、工作时间、工作效率的关系:
(1)工作量=___________
×
____________;
(2)工作时间=___________÷____________;
(3)工作效率=___________÷____________;
工作时间
工作效率
工作量
工作效率
工作量
工作时间
知识复习
问题1.小学我们学过工程问题,请回答下列问题.
(1)一项工作甲单独做需要5天完成,乙单独做需要10天完成,那么甲每天的工作效率是____,乙每天的工作效率是____,两人合作3天完成的工作量是_________,此时剩余的工作量是_____.
复习提问
(2)一项工作甲单独做需要a天完成,乙单独做需要b天完成,那么甲每天的工作效率是____,乙每天的工作效率是____,两人合作3天完成的工作量是_________,此时剩余的工作量是_________.
复习提问
问题1.小学我们学过工程问题,请回答下列问题.
归纳小结:
为简便起见,通常设总工作量为“1”.
1.如果已知工作时间,
那么“时间的倒数”就是工作效率.
知识归纳
2.如果工程为多方合作完成,
则合作完成时的工作效率是各方的工作效率相加.
例1:一件工作,甲单独做15小时完成,乙单独做
10小时完成.那么两人合作多少小时完成?
甲
乙
工作效率
工作时间
工作量
X
X
甲的工作量
+
乙的工作量
=
工作总量1
甲的工作量
+
乙的工作量
=
工作总量1
解:设两人合作x小时完成此工作,
依题意,得:
答:两人合作6小时完成.?
去分母,得
4x+6x=60
合并同类项,得
10x=60
系数化为1,得
x=6
变式1:一件工作,甲单独做15小时完成,乙单独做10
小时完成.甲先单独做9小时,后因甲有其它任务
调离,余下的任务由乙单独完成。那么乙还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
9
X
甲的工作量
+
乙的工作量
=
工作总量1
答:乙还要4小时完成.
解:设乙还需x小时完成此工作,依题意,得:
解得
x=4
变式2:一件工作,甲单独做15小时完成,乙单独做
12小时完成.甲先单独做6小时,然后乙加入
合作,那么两人合作还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
X+6
X
甲的工作量
+
乙的工作量
=
工作总量1
甲的工作量
+
乙的工作量
=
工作总量1
答:两人合作还要4小时完成.
解:设两人合作还需x小时完成此工作,
依题意,得:
解得
x=4
变式3:一件工作,甲单独做15小时完成,甲、乙合做
6小时完成.甲先单独做6小时,余下的乙单独做,那么乙还要多少小时完成?
甲
乙
工作效率
工作时间
工作量
6
X
甲的工作量
+
乙的工作量
=
工作总量1
答:乙还要6小时完成.
解:设乙还需x小时完成此工作,依题意,得:
解得
x=6
列表分析:
问题探究
例2:整理一批图书,由一个人做要40h完成.现计划由一部分人先做4
h,然后增加
2人与他们一起做8
h,完成这项工作.
假设这些人的工作效率相同,具体应该先安排多少人工作?
列表分析:
人均效率
人数
时间
工作量
前一部分工作
后一部分工作
×
=
×
×
×
=
问题探究
(x+2)
x
4
8
解:设安排
x
人先做4
h.
依题意得,
.
解方程得
,
4x+8(x+2)=40,
4x+8x+16=40,
12x=24,
x=2.
答:应安排
2人先做4
h.
问题探究
例3:某工厂接受了加工一批零件的任务,按原来每天的定额,预计30天可以完成。由于进行了技术革新,工作效率比原来提高了50%,结果提前8天完成任务,并且多加工了24件,原来接受的加工任务是多少?原来每天加工的定额是多少?
原来
实际
工作效率
工作时间
工作量
30
30-8
1.一条地下管线由甲工程队单独铺设需要
12天完成,由乙工程队单独铺设需要24天完成.
如果由这两个工程队从两端同时施工,需要多少天才能完成这条管线的铺设任务?
解:设两个工程队合作施工,
x天可以铺好这条管线.
依题意,得
解方程,得
x=8.
答:两个工程队从两端同时施工,需要8天才能完成这条管线的铺设任务.
巩固练习
2.收割一块水稻田,若每小时收割4亩,预计若干小时完成,收割
后,改用新式农机,工作效率提高到原来的
倍,因此比预计时间提早1小时完成.求这块水稻田的面积.
巩固练习
解:设这块水稻田的面积为x亩.
依题意,得
.
解方程,得
x=36.
答:这块水稻田的面积为36亩.
巩固练习
用一元一次方程解决实际问题的基本过程有几个步骤?分别是什么?
实际问题
一元一次方程
设未知数,列方程
解方程
一元一次方程的解(x
=
a)
实际问题的答案
检
验
探究
课堂小结
1.本节课学习的主要内容是什么?
2.分析实际问题中的数量关系,常用的方法是什么?需要注意哪些问题?
3.通过本节课的学习,尝试用自己的语言描述,如何建立方程模型来解决实际问题?
