人教版数学九年级上册 24.2.1点和圆的位置关系课件(共22张ppt)
文档属性
| 名称 | 人教版数学九年级上册 24.2.1点和圆的位置关系课件(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 12:52:32 | ||
图片预览






文档简介
(共22张PPT)
24.2 点和圆、直线和圆的
位置关系(第1课时)
九年级 上册
学习目标:
1.理解点和圆的三种位置关系,并会运用它解决一
些实际问题;
2.会过不在同一直线上的三个点作圆,理解三角形
的外心和外接圆的概念;
3.结合本节内容的学习,体会数形结合、分类讨论
的数学思想.
学习重点:
点和圆的位置关系.
课件说明
一.导入新知
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉,如图它是由许多同心圆(圆心
、半径
的圆)
构成的,你知道击中靶上不同位置的成绩是如何计算的吗?(和同学交流一下)
相同
不同
1:结合上面的问题,你能试着说出点和圆有哪些位置关系吗?
2:对于点和圆的位置关系,能从数量关系的角度进行
刻画吗?
2.探究新知
知识点1:
探究点和圆的位置关系
点在
,
点在
,
点在
.
圆上
圆外
圆内
2.探究新知
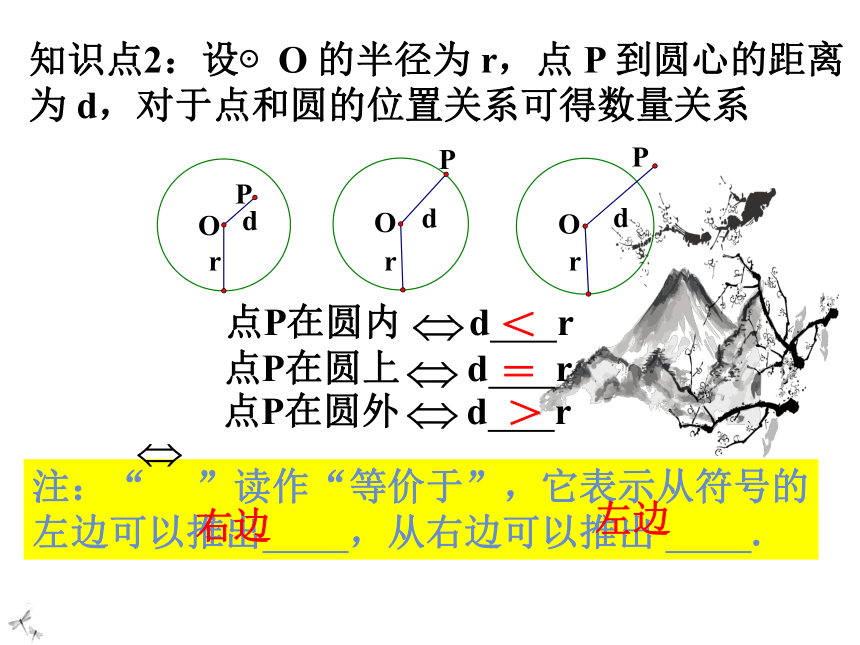
知识点2:设⊙O
的半径为
r,点
P
到圆心的距离为
d,对于点和圆的位置关系可得数量关系
O
d
r
P
O
d
r
P
O
d
r
P
点P在圆内
d
r
点P在圆上
d
r
点P在圆外
d
r
<
=
>
注:“
”读作“等价于”,它表示从符号的左边可以推出
,从右边可以推出
.
右边
左边
·
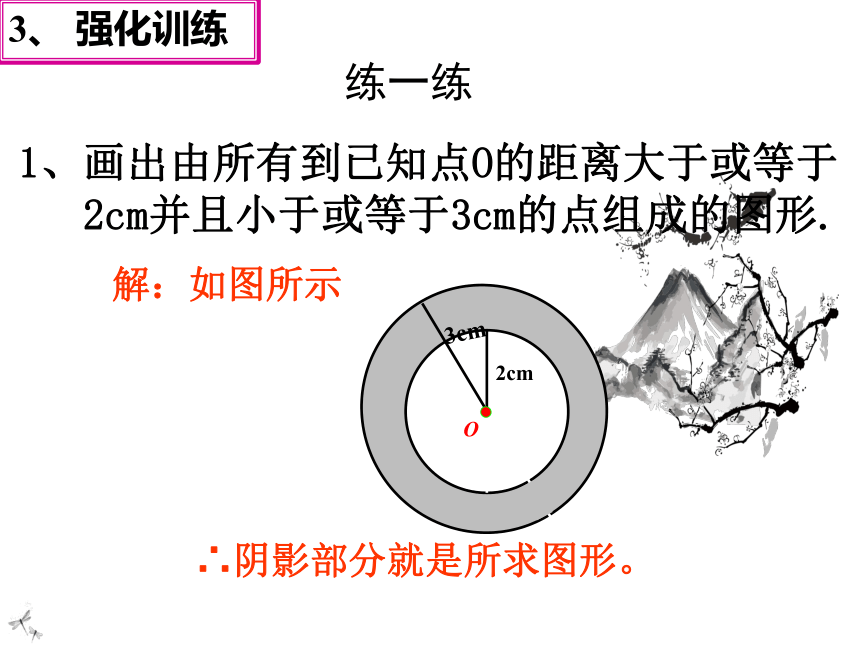
1、画出由所有到已知点O的距离大于或等于
2cm并且小于或等于3cm的点组成的图形.
·
O
2cm
3cm
解:如图所示
∴阴影部分就是所求图形。
练一练
3、
强化训练
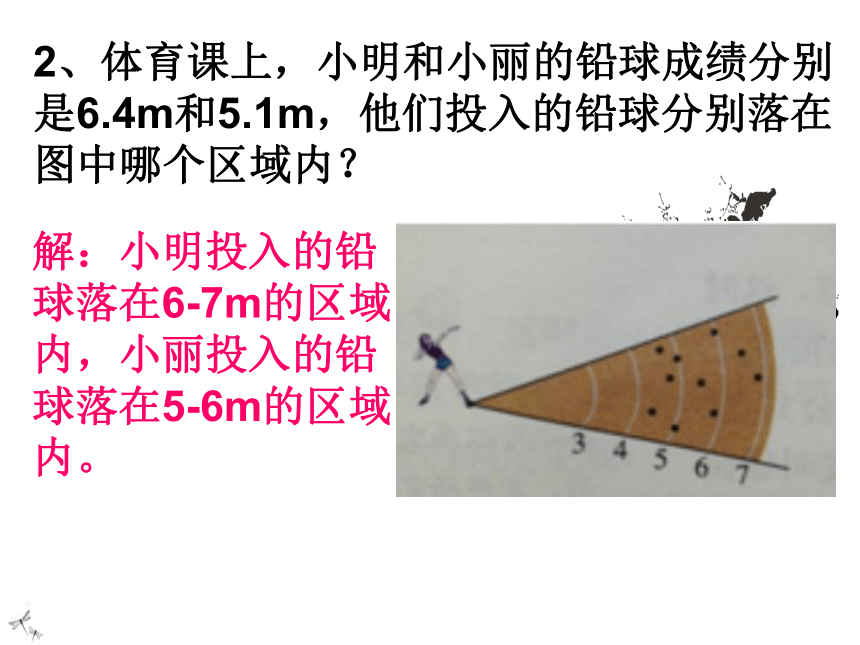
2、体育课上,小明和小丽的铅球成绩分别是6.4m和5.1m,他们投入的铅球分别落在图中哪个区域内?
解:小明投入的铅球落在6-7m的区域内,小丽投入的铅球落在5-6m的区域内。
我们知道,已知圆心和半径,可以作一个圆.
那么经过几个已知点,可以作圆吗?如果能,可以做几个圆?
4、研学教材
·
1、如图①
经过一个已知点A作圆
·
O2
r2
①
O1
r1
·
O3
r3
·
O4
r4
·
O5
r5
A
解:如图所示
2、如图②
经过两个已知点A、B作圆
②
·
O2
r2
·
O1
r1
r3
O3
·
·
O4
r4
O5
·
r5
B
A
解:如图所示
结论:
1、经过一点可以作
个圆.
2、经过两点A、B可以作
个圆,这
些圆的圆心分布在
_________
____
上.
无数
无数
以这两个点为端点的
线段的垂直平分线
已知点
A、B、C
已知三点共线
已知三点不共线
3、
经过三个已知点A、B、C作圆
①
连接
AB、BC;
②
分别作线段
AB、BC
的垂直平分线DE
和
FG,DE
和FG
相交于点
O;
③
以点O
为圆心,OA
为半径作圆,⊙O
就是所要求作的圆.
O
A
B
C
D
E
F
G
1、如何经过不在同一条直线上的三个点
A、B、C
作圆?
1、经过三角形的三个顶点可以作
圆,
这个圆叫做三角形的
圆.
2、外接圆的圆心是三角形三条边_
_
_
_的交点,叫做这个三角形的
.
一个
外接
垂直平分线
外心
练一练
下列语句
①三角形的外心是各边垂直平分线的交点;
②三角形的外心到三角形三边的距离相等;
③等腰三角形的外心一定在这个三角形内.
正确的是
.
①
③
强化训练
反证法
1、不是直接从命题的已知得出结论,而
是假设命题的结论
,由此经
过推理得出矛盾,由矛盾断定所作假
设不正确,从而得到命题成立.这种
证明方法叫做
.
不成立
反证法
4、研学教材
用反证法的证明:
经过同一条直线上的点不能作出一个圆.
证明:如图假设过同一直线L上的
A、B、C三点可以作一个圆,
设这个圆的圆心为P,那么点P既在
线段AB的垂直平分线L1,又在线段
的垂直平分线L2,即点P为L1与
L2的
点,而L1⊥L,L2⊥L,这
与我们以前所学的“过一点有且只
有
条直线与已知直线
”矛
盾.所以,过同一直线上的三点不能作圆.
BC
交
一
垂直
4、研学教材
例1 已知⊙O
的半径为
5,圆心
O
的坐标为
(0,0),若点
P
的坐标为(4,2),点
P
与⊙O
的位置关系是(
).
A.点
P
在⊙O
内 B.点
P
在⊙O上
C.点
P
在⊙O
外 D.点
P
在⊙O
上或⊙O
外
5.应用举例
例2 直角三角形的外心是______的中点,
锐角三角形的外心在三角形______,钝角三角形的外心在三角形_________.
例4、如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.
例3、过在同一平面上的三点
(填“一定”或“不一定”)可以画一个圆.
O
A
B
C
D
不一定
解:如图所示
1、点和圆的位置关系有:
_________________________________.
2、经过一点可以作_____个圆;经过两点可以作_____个圆,经过不在同一直线上的三个点可以作___个圆.
3、三角形的外心是
的交点.
⑴.点在圆上
⑵.点在圆内
⑶.点在圆外
无数
无数
一
三角形三边垂直平分线
6.课堂小结
教科书第
95
页 练习第
2,3
题.
5.布置作业
24.2 点和圆、直线和圆的
位置关系(第1课时)
九年级 上册
学习目标:
1.理解点和圆的三种位置关系,并会运用它解决一
些实际问题;
2.会过不在同一直线上的三个点作圆,理解三角形
的外心和外接圆的概念;
3.结合本节内容的学习,体会数形结合、分类讨论
的数学思想.
学习重点:
点和圆的位置关系.
课件说明
一.导入新知
我国射击运动员在奥运会上屡获金牌,为祖国赢得荣誉,如图它是由许多同心圆(圆心
、半径
的圆)
构成的,你知道击中靶上不同位置的成绩是如何计算的吗?(和同学交流一下)
相同
不同
1:结合上面的问题,你能试着说出点和圆有哪些位置关系吗?
2:对于点和圆的位置关系,能从数量关系的角度进行
刻画吗?
2.探究新知
知识点1:
探究点和圆的位置关系
点在
,
点在
,
点在
.
圆上
圆外
圆内
2.探究新知
知识点2:设⊙O
的半径为
r,点
P
到圆心的距离为
d,对于点和圆的位置关系可得数量关系
O
d
r
P
O
d
r
P
O
d
r
P
点P在圆内
d
r
点P在圆上
d
r
点P在圆外
d
r
<
=
>
注:“
”读作“等价于”,它表示从符号的左边可以推出
,从右边可以推出
.
右边
左边
·
1、画出由所有到已知点O的距离大于或等于
2cm并且小于或等于3cm的点组成的图形.
·
O
2cm
3cm
解:如图所示
∴阴影部分就是所求图形。
练一练
3、
强化训练
2、体育课上,小明和小丽的铅球成绩分别是6.4m和5.1m,他们投入的铅球分别落在图中哪个区域内?
解:小明投入的铅球落在6-7m的区域内,小丽投入的铅球落在5-6m的区域内。
我们知道,已知圆心和半径,可以作一个圆.
那么经过几个已知点,可以作圆吗?如果能,可以做几个圆?
4、研学教材
·
1、如图①
经过一个已知点A作圆
·
O2
r2
①
O1
r1
·
O3
r3
·
O4
r4
·
O5
r5
A
解:如图所示
2、如图②
经过两个已知点A、B作圆
②
·
O2
r2
·
O1
r1
r3
O3
·
·
O4
r4
O5
·
r5
B
A
解:如图所示
结论:
1、经过一点可以作
个圆.
2、经过两点A、B可以作
个圆,这
些圆的圆心分布在
_________
____
上.
无数
无数
以这两个点为端点的
线段的垂直平分线
已知点
A、B、C
已知三点共线
已知三点不共线
3、
经过三个已知点A、B、C作圆
①
连接
AB、BC;
②
分别作线段
AB、BC
的垂直平分线DE
和
FG,DE
和FG
相交于点
O;
③
以点O
为圆心,OA
为半径作圆,⊙O
就是所要求作的圆.
O
A
B
C
D
E
F
G
1、如何经过不在同一条直线上的三个点
A、B、C
作圆?
1、经过三角形的三个顶点可以作
圆,
这个圆叫做三角形的
圆.
2、外接圆的圆心是三角形三条边_
_
_
_的交点,叫做这个三角形的
.
一个
外接
垂直平分线
外心
练一练
下列语句
①三角形的外心是各边垂直平分线的交点;
②三角形的外心到三角形三边的距离相等;
③等腰三角形的外心一定在这个三角形内.
正确的是
.
①
③
强化训练
反证法
1、不是直接从命题的已知得出结论,而
是假设命题的结论
,由此经
过推理得出矛盾,由矛盾断定所作假
设不正确,从而得到命题成立.这种
证明方法叫做
.
不成立
反证法
4、研学教材
用反证法的证明:
经过同一条直线上的点不能作出一个圆.
证明:如图假设过同一直线L上的
A、B、C三点可以作一个圆,
设这个圆的圆心为P,那么点P既在
线段AB的垂直平分线L1,又在线段
的垂直平分线L2,即点P为L1与
L2的
点,而L1⊥L,L2⊥L,这
与我们以前所学的“过一点有且只
有
条直线与已知直线
”矛
盾.所以,过同一直线上的三点不能作圆.
BC
交
一
垂直
4、研学教材
例1 已知⊙O
的半径为
5,圆心
O
的坐标为
(0,0),若点
P
的坐标为(4,2),点
P
与⊙O
的位置关系是(
).
A.点
P
在⊙O
内 B.点
P
在⊙O上
C.点
P
在⊙O
外 D.点
P
在⊙O
上或⊙O
外
5.应用举例
例2 直角三角形的外心是______的中点,
锐角三角形的外心在三角形______,钝角三角形的外心在三角形_________.
例4、如图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心.
例3、过在同一平面上的三点
(填“一定”或“不一定”)可以画一个圆.
O
A
B
C
D
不一定
解:如图所示
1、点和圆的位置关系有:
_________________________________.
2、经过一点可以作_____个圆;经过两点可以作_____个圆,经过不在同一直线上的三个点可以作___个圆.
3、三角形的外心是
的交点.
⑴.点在圆上
⑵.点在圆内
⑶.点在圆外
无数
无数
一
三角形三边垂直平分线
6.课堂小结
教科书第
95
页 练习第
2,3
题.
5.布置作业
同课章节目录
