2020-2021学年北师大新版九年级下册数学《第3章 圆》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年北师大新版九年级下册数学《第3章 圆》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 442.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 22:24:57 | ||
图片预览


文档简介
2020-2021学年北师大新版九年级下册数学《第3章
圆》单元测试卷
一.选择题
1.已知⊙O中最长的弦长8cm,则⊙O的半径是( )
A.2cm
B.4cm
C.8cm
D.16cm
2.如图,AB是⊙O的直径,O为圆心,C是⊙O上的点,D是上的点,若∠D=120°,则∠BOC的大小为( )
A.60°
B.55°
C.58°
D.40°
3.关于下列四种说法中,你认为正确的有( )
①垂直于弦的直线一定经过圆心;
②经过直径外端的直线是圆的切线;
③对角互补的四边形四个顶点共圆;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分.
A.1个
B.2个
C.3个
D.4个
4.如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
A.50m
B.45m
C.40m
D.60m
5.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25°
B.50°
C.65°
D.75°
6.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则△OFC的面积是( )
A.40cm2
B.20cm2
C.10cm2
D.5cm2
7.在矩形ABCD中,AB=3,AD=5,以点A为圆心,4为半径作圆,点C与⊙A的位置关系( )
A.点C在⊙A内
B.点C在⊙A上
C.点C在⊙A外
D.无法确定
8.如图,PA,PB分别切⊙O与点A,B,MN切⊙O于点C,分别交PA,PB于点M,N,若PA=7.5cm,则△PMN的周长是( )
A.7.5cm
B.10cm
C.12.5cm
D.15cm
9.⊙O的内接多边形周长为5,⊙O的外切多边形周长为3,则下列各数中与此圆的周长最接近的是( )
A.π
B.2π
C.3π
D.4π
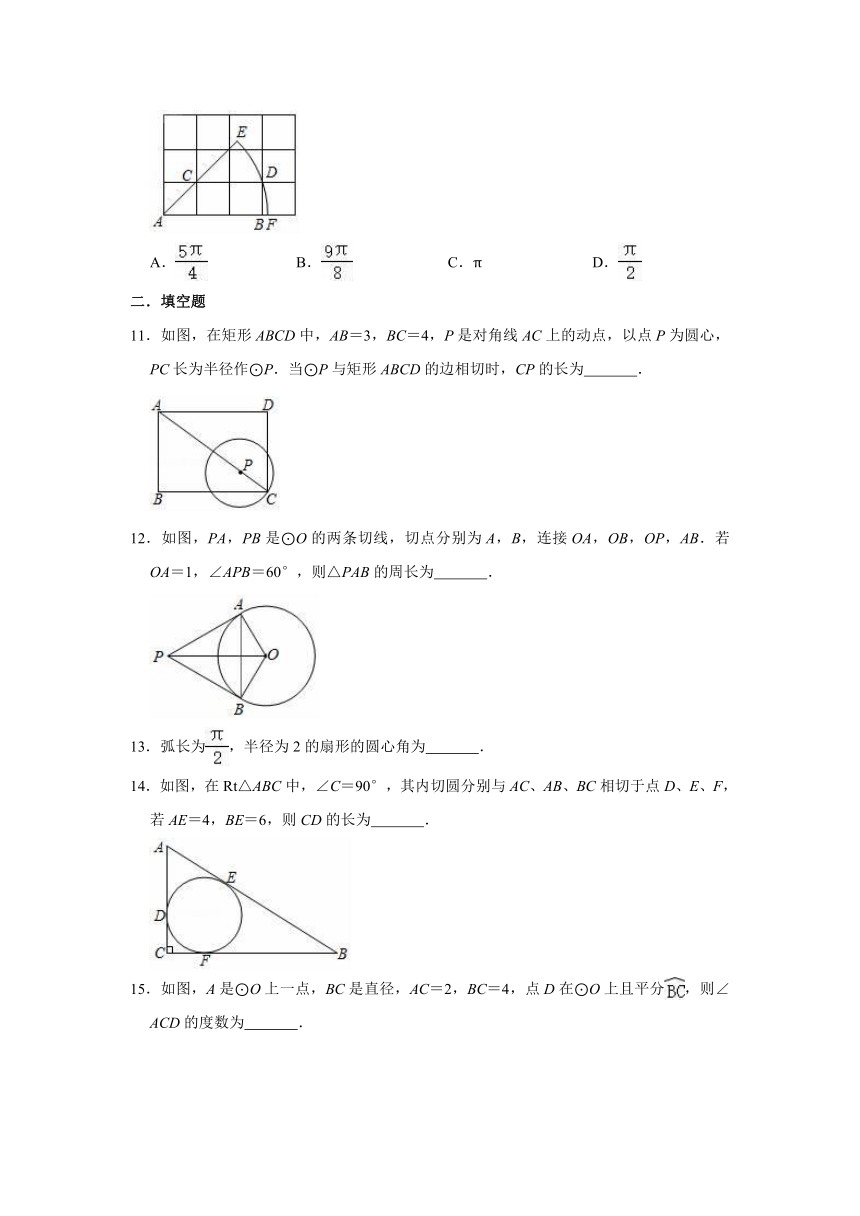
10.如图,点A、B、C、D都在边长为1的网格格点上,以A为圆心,AE为半径画弧,弧EF经过格点D,则扇形AEF的面积是( )
A.
B.
C.π
D.
二.填空题
11.如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,以点P为圆心,PC长为半径作⊙P.当⊙P与矩形ABCD的边相切时,CP的长为
.
12.如图,PA,PB是⊙O的两条切线,切点分别为A,B,连接OA,OB,OP,AB.若OA=1,∠APB=60°,则△PAB的周长为
.
13.弧长为,半径为2的扇形的圆心角为
.
14.如图,在Rt△ABC中,∠C=90°,其内切圆分别与AC、AB、BC相切于点D、E、F,若AE=4,BE=6,则CD的长为
.
15.如图,A是⊙O上一点,BC是直径,AC=2,BC=4,点D在⊙O上且平分,则∠ACD的度数为
.
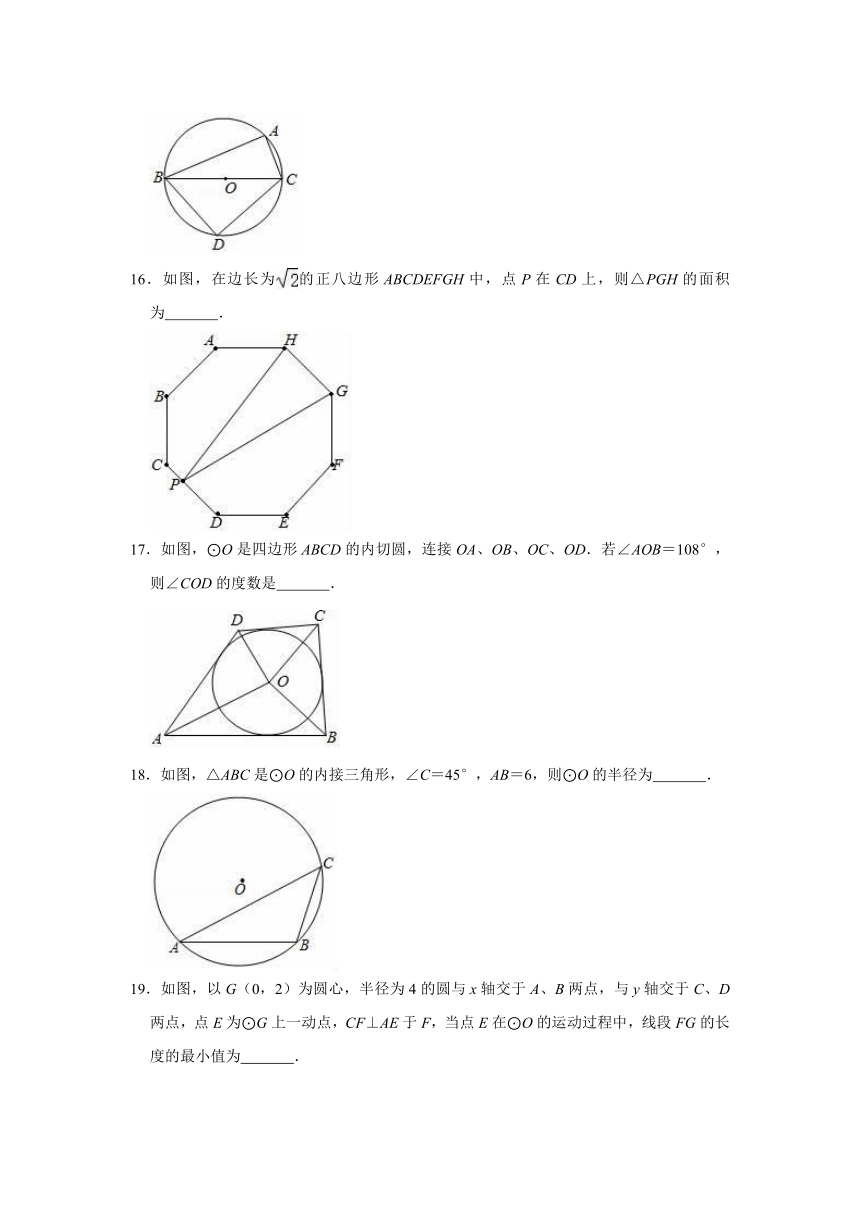
16.如图,在边长为的正八边形ABCDEFGH中,点P在CD上,则△PGH的面积为
.
17.如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=108°,则∠COD的度数是
.
18.如图,△ABC是⊙O的内接三角形,∠C=45°,AB=6,则⊙O的半径为
.
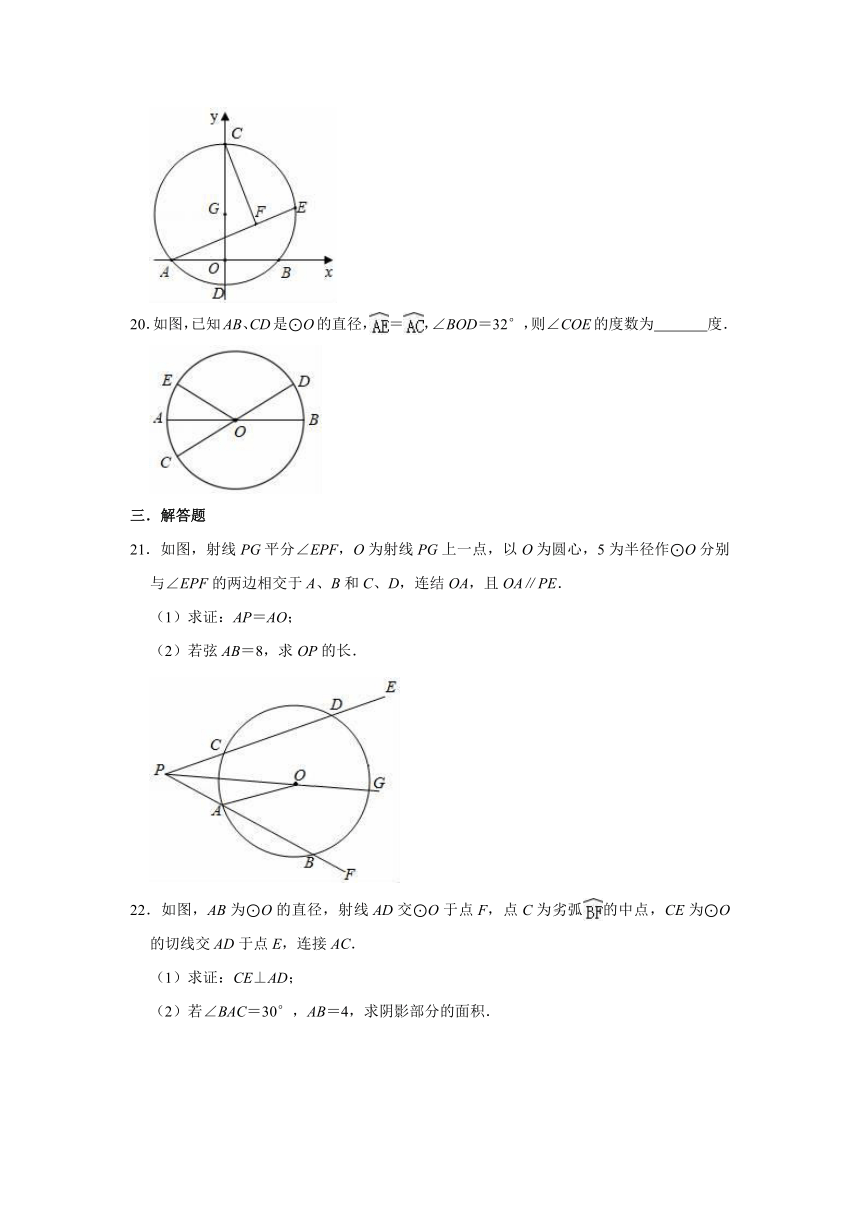
19.如图,以G(0,2)为圆心,半径为4的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E在⊙O的运动过程中,线段FG的长度的最小值为
.
20.如图,已知AB、CD是⊙O的直径,=,∠BOD=32°,则∠COE的度数为
度.
三.解答题
21.如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,5为半径作⊙O分别与∠EPF的两边相交于A、B和C、D,连结OA,且OA∥PE.
(1)求证:AP=AO;
(2)若弦AB=8,求OP的长.
22.如图,AB为⊙O的直径,射线AD交⊙O于点F,点C为劣弧的中点,CE为⊙O的切线交AD于点E,连接AC.
(1)求证:CE⊥AD;
(2)若∠BAC=30°,AB=4,求阴影部分的面积.
23.如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
24.如图AB=3cm,用图形表示:到点A的距离小于2cm,且到点B的距离不小于2cm的所有点的集合(用阴影表示,注意边界上的点是否在集合中,如果在,用实线表示,如果不在,则用虚线表示).
25.如图:,CD⊥OA于D,CE⊥OB于E,求证:CD=CE.
26.如图,AB是⊙O的直径,点C在⊙O上,半径OD⊥AC,DE⊥AB于点E,交弦AC于点F,连接BD,AD,
(1)若∠ABD=25°,求∠DAC的度数(提示:半径OD⊥AC,可根据垂径定理解题);
(2)求证:DF=AF.
27.如图,△ABC内接于⊙O,AD⊥BC于点D,AD=BD,AE为⊙O直径,⊙O的半径为2,连接BE.
(1)求AC的长;
(2)求证:BE=DC.
参考答案与试题解析
一.选择题
1.解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
2.解:∵∠D=120°,
∴∠B=60°,
∵CO=BO,
∴△COB是等边三角形,
∴∠COB=60°,
故选:A.
3.解:①垂直平分弦的直线经过圆心,故①不符合题意;
②经过直径外端切垂直于这条直径的直线是圆的切线,故②不符合题意;
③对角互补的四边形四个顶点共圆;故③符合题意;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分,故④符合题意;
故选:B.
4.解:设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,如图所示:
则OA=OD=250,AC=BC=AB=150,
∴OC===200,
∴CD=OD﹣OC=250﹣200=50(m),
即这些钢索中最长的一根为50m,
故选:A.
5.解:∵根据圆周角定理得:∠AOC=2∠ABC,
∵∠ABC+∠AOC=75°,
∴∠AOC=×75°=50°,
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,
故选:C.
6.解:连接OB,如图所示:
设⊙O的半径为rcm,则OE=(r﹣2)cm,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,
∴BE=DE=4(cm),
在Rt△OBE中,∵OE2+BE2=OB2
,
∴(r﹣2)2+42=r2
解得:r=5,
∴AC=10(cm),EC=AC﹣AE=8(cm),
∴BC===4(cm),
∵OF⊥BC,
∴CF=BF=BC=2(cm),
∴OF===(cm),
∴△OFC的面积=CF×OF=×2×=5(cm2),
故选:D.
7.解:由勾股定理,得
AC===,
∵AC>r,
点C与⊙A外边,
故选:C.
8.解:∵直线PA、PB、MN分别与⊙O相切于点A、B、C,
∴MA=MC,NC=NB,
∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=PA+PB=7.5+7.5=15(cm).
故选:D.
9.解:圆外切多边形的周长大于圆周长,圆内接多边形的周长小于圆周长.
圆的内接多边形周长为5,外切多边形周长为3,所以圆周长在9与12之间.
只有只有C选项满足条件.
故选:C.
10.解:由题意,扇形的半径AD==,∠EAF=45°,
∴扇形AEF的面积==.
故选:A.
二.填空题
11.解:作PE⊥AD于E,PF⊥AB于F,
在Rt△ABC中,AC==5,
由题意可知,⊙P只能与矩形ABCD的边AD、AB相切,
当⊙P与AD相切时,PE=PC,
∵PE⊥AD,CD⊥AD,
∴PE∥CD,
∴△APE∽△ACD,
∴=,即=,
解得,CP=,
当⊙P与AB相切时,PF=PC,
∵PF⊥AB,CB⊥AB,
∴PF∥BC,
∴△APE∽△ACD,
∴=,即=,
解得,CP=,
综上所述,当⊙P与矩形ABCD的边相切时,CP的长或,
故答案为:或.
12.解:∵PA,PB是⊙O的两条切线,
∴PA=PB,OA⊥PA,OP平分∠APB,
∵∠APB=60°,
∴∠APO=∠APB=30°,△PAB为等边三角形,
在Rt△OAP中,∵∠APO=30°,
∴PA=OA=,
∴△PAB的周长=3PA=3.
故答案为3.
13.解:∵扇形的弧长为,半径为2,
∴=,
解得:n=45°.
故答案为45°.
14.解:∵Rt△ABC的内切圆分别与AC、AB、BC相切于点D、E、F,
∴AD=AE=4,BF=BE=6,CD=CF,
∵∠C=90°,
∴AC2+BC2=AB2,
∴(4+CD)2+(CD+6)2=(4+6)2,
解得:CD=﹣12(舍)或2,
故答案为:2.
15.解:∵BC是⊙O的直径,
∴∠BAC=∠D=90°,
∵AC=2,AB=4,
∴cos∠ACB==,
∴∠ACB=60°,
又∵点D在⊙O上且平分,
∴,
∴BD=CD,
∴△BCD是等腰直角三角形,
∴∠DCB=∠DBC=45°,
∴∠ACD=∠ACB+∠DCB=105°,
故答案为:105°.
16.解:作正八边形的外接圆O,
则∠HGD=×360°=90°,∠FGD=×360°=45°,
在正八边形ABCDEFGH中,CD∥HG,
∴S△HGP=S△CDH,
过F作FM⊥DG于M,过E作EN⊥DG于N,
在Rt△GMF中,∠FGD=45°,GF=,
∴GM=GF=1,
同理,DN=1,
∵MN=EF=,
∴GD=1++1=2+,
∴S△HGP=S△HGD=HG?GD=.
故答案为:
+1.
17.解:如图所示:连接圆心与各切点,
在Rt△DEO和Rt△DFO中,
∴Rt△DEO≌Rt△DFO(HL),
∴∠1=∠2,
同理可得:Rt△AFO≌Rt△AMO,Rt△BMO≌Rt△BNO,Rt△CEO≌Rt△CNO,
∴∠3=∠4,∠5=∠7,∠6=∠8,
∴∠5+∠6=∠7+∠8=108°,
∴2∠2+2∠3=360°﹣2×108°,
∴∠2+∠3=∠DOC=72°.
故答案为:72°.
18.解:如图,连接OA,OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB,
∴△AOB是等腰直角三角形,
∴OA=OB=AB=3,
即⊙O的半径是3,
故答案为:3.
19.解:过G作GM⊥AC于M,连接AG,如图所示:
∵GO⊥AB,
∴OA=OB,
∵G(0,2),
∴OG=2,
在Rt△AGO中,∵AG=4,OG=2,
∴AG=2OG,OA==2,
∴∠GAO=30°,AB=2AO=4,
∴∠AGO=60°,
∵GC=GA=4,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=4,MG=CG=2,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣MG=2﹣2,
故答案为:2﹣2.
20.解:∵∠BOD=32°,
∴∠AOC=∠BOD=32°,
∵=,
∴∠AOE=∠AOC=32°,
∴∠COE=∠AOC+∠AOE=32°+32°=64°,
故答案为:64.
三.解答题
21.(1)证明:∵PG平分∠EPF,
∴∠DPO=∠APO,
∵OA∥PE,
∴∠DPO=∠AOP,
∴∠APO=∠AOP,
∴AP=AO;
(2)解:过O点作OH⊥AB于H,如图,则AH=BH=AB=4,
在Rt△AOH中,∵OA=5,AH=4,
∴OH==3,
∵AP=AO=5,
∴PH=PA+AH=9,
在Rt△POH中,OP==3.
22.解:(1)如图1,连接BF,OC,
∵AB是⊙O的直径,
∴∠AFB=90°,即BF⊥AD,
∵CE是⊙O的切线,OC是⊙O的半径,
∴OC⊥CE,
∵点C为劣弧的中点,
∴OC⊥BF,
∴BF∥CE,
∴CE⊥AD;
(2)如图2,连接OF,CF,
∵OA=OC,∠BAC=30°,
∴∠BOC=60°,
∵点C为劣弧的中点,
∴=,
∴∠FOC=∠BOC=60°,
∵OF=OC,
∴∠OCF=∠COB,
∴CF∥AB,
∴S△ACF=S△COF,
∴阴影部分的面积=S扇形COF,
∵AB=4,
∴FO=OC=OB=2,
∴S扇形FOC==π,
即阴影部分的面积为:π.
23.解:(1)∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB,且∠P=60°,
∴△PAB是等边三角形;
(2)∵△PAB是等边三角形;
∴PB=AB=2cm,∠PBA=60°,
∵BC是直径,PB是⊙O切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC==,
∴AC=2×=cm.
24.解:到点A的距离小于2cm,且到点B的距离不小于2cm的所有点的集合如图所示:
25.证明:∵=,
∴∠AOC=∠BOC,
∵CD⊥OA,CE⊥OB,
∴CD=CE.
26.(1)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABD=25°,
∴∠DAB=65°,∠DOA=50°,
∵OD⊥AC,
∴∠EAF=40°,
∴∠DAC=65°﹣40°=25°;
(2)证明:∵DE⊥AB于点E,
∴∠DEO=90°,
∵∠DOA=50°,
∴∠EDO=40°,
∵AO=DO,
∴∠OAD=∠ADO=65°,
∴∠ADE=65°﹣40°=25°,
∵∠DAC=25°,
∴AF=DF.
27.解:(1)如图,连接EC,
∵AD⊥BC于点D,AD=BD,
∴∠ABD=∠BAD=45°,
∴∠AEC=∠ABD=45°,
∵AE是⊙O的直径,
∴∠ACE=90°,
∵AE=4,
∴AC=AE?sin45°=4×=2;
(2)证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ABE=∠ADC,
∵∠AEB=∠ACB,
∴△ABE∽△ADC,
∴BE:DC=AE:AC=4:2=,
∴BE=DC.
圆》单元测试卷
一.选择题
1.已知⊙O中最长的弦长8cm,则⊙O的半径是( )
A.2cm
B.4cm
C.8cm
D.16cm
2.如图,AB是⊙O的直径,O为圆心,C是⊙O上的点,D是上的点,若∠D=120°,则∠BOC的大小为( )
A.60°
B.55°
C.58°
D.40°
3.关于下列四种说法中,你认为正确的有( )
①垂直于弦的直线一定经过圆心;
②经过直径外端的直线是圆的切线;
③对角互补的四边形四个顶点共圆;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分.
A.1个
B.2个
C.3个
D.4个
4.如图,武汉晴川桥可以近似地看作半径为250m的圆弧,桥拱和路面之间用数根钢索垂直相连,其正下方的路面AB长度为300m,那么这些钢索中最长的一根为( )
A.50m
B.45m
C.40m
D.60m
5.如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A.25°
B.50°
C.65°
D.75°
6.如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则△OFC的面积是( )
A.40cm2
B.20cm2
C.10cm2
D.5cm2
7.在矩形ABCD中,AB=3,AD=5,以点A为圆心,4为半径作圆,点C与⊙A的位置关系( )
A.点C在⊙A内
B.点C在⊙A上
C.点C在⊙A外
D.无法确定
8.如图,PA,PB分别切⊙O与点A,B,MN切⊙O于点C,分别交PA,PB于点M,N,若PA=7.5cm,则△PMN的周长是( )
A.7.5cm
B.10cm
C.12.5cm
D.15cm
9.⊙O的内接多边形周长为5,⊙O的外切多边形周长为3,则下列各数中与此圆的周长最接近的是( )
A.π
B.2π
C.3π
D.4π
10.如图,点A、B、C、D都在边长为1的网格格点上,以A为圆心,AE为半径画弧,弧EF经过格点D,则扇形AEF的面积是( )
A.
B.
C.π
D.
二.填空题
11.如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,以点P为圆心,PC长为半径作⊙P.当⊙P与矩形ABCD的边相切时,CP的长为
.
12.如图,PA,PB是⊙O的两条切线,切点分别为A,B,连接OA,OB,OP,AB.若OA=1,∠APB=60°,则△PAB的周长为
.
13.弧长为,半径为2的扇形的圆心角为
.
14.如图,在Rt△ABC中,∠C=90°,其内切圆分别与AC、AB、BC相切于点D、E、F,若AE=4,BE=6,则CD的长为
.
15.如图,A是⊙O上一点,BC是直径,AC=2,BC=4,点D在⊙O上且平分,则∠ACD的度数为
.
16.如图,在边长为的正八边形ABCDEFGH中,点P在CD上,则△PGH的面积为
.
17.如图,⊙O是四边形ABCD的内切圆,连接OA、OB、OC、OD.若∠AOB=108°,则∠COD的度数是
.
18.如图,△ABC是⊙O的内接三角形,∠C=45°,AB=6,则⊙O的半径为
.
19.如图,以G(0,2)为圆心,半径为4的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E在⊙O的运动过程中,线段FG的长度的最小值为
.
20.如图,已知AB、CD是⊙O的直径,=,∠BOD=32°,则∠COE的度数为
度.
三.解答题
21.如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,5为半径作⊙O分别与∠EPF的两边相交于A、B和C、D,连结OA,且OA∥PE.
(1)求证:AP=AO;
(2)若弦AB=8,求OP的长.
22.如图,AB为⊙O的直径,射线AD交⊙O于点F,点C为劣弧的中点,CE为⊙O的切线交AD于点E,连接AC.
(1)求证:CE⊥AD;
(2)若∠BAC=30°,AB=4,求阴影部分的面积.
23.如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
24.如图AB=3cm,用图形表示:到点A的距离小于2cm,且到点B的距离不小于2cm的所有点的集合(用阴影表示,注意边界上的点是否在集合中,如果在,用实线表示,如果不在,则用虚线表示).
25.如图:,CD⊥OA于D,CE⊥OB于E,求证:CD=CE.
26.如图,AB是⊙O的直径,点C在⊙O上,半径OD⊥AC,DE⊥AB于点E,交弦AC于点F,连接BD,AD,
(1)若∠ABD=25°,求∠DAC的度数(提示:半径OD⊥AC,可根据垂径定理解题);
(2)求证:DF=AF.
27.如图,△ABC内接于⊙O,AD⊥BC于点D,AD=BD,AE为⊙O直径,⊙O的半径为2,连接BE.
(1)求AC的长;
(2)求证:BE=DC.
参考答案与试题解析
一.选择题
1.解:∵⊙O中最长的弦为8cm,即直径为8cm,
∴⊙O的半径为4cm.
故选:B.
2.解:∵∠D=120°,
∴∠B=60°,
∵CO=BO,
∴△COB是等边三角形,
∴∠COB=60°,
故选:A.
3.解:①垂直平分弦的直线经过圆心,故①不符合题意;
②经过直径外端切垂直于这条直径的直线是圆的切线,故②不符合题意;
③对角互补的四边形四个顶点共圆;故③符合题意;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分,故④符合题意;
故选:B.
4.解:设圆弧的圆心为O,过O作OC⊥AB于C,交于D,连接OA,如图所示:
则OA=OD=250,AC=BC=AB=150,
∴OC===200,
∴CD=OD﹣OC=250﹣200=50(m),
即这些钢索中最长的一根为50m,
故选:A.
5.解:∵根据圆周角定理得:∠AOC=2∠ABC,
∵∠ABC+∠AOC=75°,
∴∠AOC=×75°=50°,
∵OA=OC,
∴∠OAC=∠OCA=(180°﹣∠AOC)=65°,
故选:C.
6.解:连接OB,如图所示:
设⊙O的半径为rcm,则OE=(r﹣2)cm,
∵AC是⊙O的直径,弦BD⊥AO于E,BD=8cm,
∴BE=DE=4(cm),
在Rt△OBE中,∵OE2+BE2=OB2
,
∴(r﹣2)2+42=r2
解得:r=5,
∴AC=10(cm),EC=AC﹣AE=8(cm),
∴BC===4(cm),
∵OF⊥BC,
∴CF=BF=BC=2(cm),
∴OF===(cm),
∴△OFC的面积=CF×OF=×2×=5(cm2),
故选:D.
7.解:由勾股定理,得
AC===,
∵AC>r,
点C与⊙A外边,
故选:C.
8.解:∵直线PA、PB、MN分别与⊙O相切于点A、B、C,
∴MA=MC,NC=NB,
∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=PA+PB=7.5+7.5=15(cm).
故选:D.
9.解:圆外切多边形的周长大于圆周长,圆内接多边形的周长小于圆周长.
圆的内接多边形周长为5,外切多边形周长为3,所以圆周长在9与12之间.
只有只有C选项满足条件.
故选:C.
10.解:由题意,扇形的半径AD==,∠EAF=45°,
∴扇形AEF的面积==.
故选:A.
二.填空题
11.解:作PE⊥AD于E,PF⊥AB于F,
在Rt△ABC中,AC==5,
由题意可知,⊙P只能与矩形ABCD的边AD、AB相切,
当⊙P与AD相切时,PE=PC,
∵PE⊥AD,CD⊥AD,
∴PE∥CD,
∴△APE∽△ACD,
∴=,即=,
解得,CP=,
当⊙P与AB相切时,PF=PC,
∵PF⊥AB,CB⊥AB,
∴PF∥BC,
∴△APE∽△ACD,
∴=,即=,
解得,CP=,
综上所述,当⊙P与矩形ABCD的边相切时,CP的长或,
故答案为:或.
12.解:∵PA,PB是⊙O的两条切线,
∴PA=PB,OA⊥PA,OP平分∠APB,
∵∠APB=60°,
∴∠APO=∠APB=30°,△PAB为等边三角形,
在Rt△OAP中,∵∠APO=30°,
∴PA=OA=,
∴△PAB的周长=3PA=3.
故答案为3.
13.解:∵扇形的弧长为,半径为2,
∴=,
解得:n=45°.
故答案为45°.
14.解:∵Rt△ABC的内切圆分别与AC、AB、BC相切于点D、E、F,
∴AD=AE=4,BF=BE=6,CD=CF,
∵∠C=90°,
∴AC2+BC2=AB2,
∴(4+CD)2+(CD+6)2=(4+6)2,
解得:CD=﹣12(舍)或2,
故答案为:2.
15.解:∵BC是⊙O的直径,
∴∠BAC=∠D=90°,
∵AC=2,AB=4,
∴cos∠ACB==,
∴∠ACB=60°,
又∵点D在⊙O上且平分,
∴,
∴BD=CD,
∴△BCD是等腰直角三角形,
∴∠DCB=∠DBC=45°,
∴∠ACD=∠ACB+∠DCB=105°,
故答案为:105°.
16.解:作正八边形的外接圆O,
则∠HGD=×360°=90°,∠FGD=×360°=45°,
在正八边形ABCDEFGH中,CD∥HG,
∴S△HGP=S△CDH,
过F作FM⊥DG于M,过E作EN⊥DG于N,
在Rt△GMF中,∠FGD=45°,GF=,
∴GM=GF=1,
同理,DN=1,
∵MN=EF=,
∴GD=1++1=2+,
∴S△HGP=S△HGD=HG?GD=.
故答案为:
+1.
17.解:如图所示:连接圆心与各切点,
在Rt△DEO和Rt△DFO中,
∴Rt△DEO≌Rt△DFO(HL),
∴∠1=∠2,
同理可得:Rt△AFO≌Rt△AMO,Rt△BMO≌Rt△BNO,Rt△CEO≌Rt△CNO,
∴∠3=∠4,∠5=∠7,∠6=∠8,
∴∠5+∠6=∠7+∠8=108°,
∴2∠2+2∠3=360°﹣2×108°,
∴∠2+∠3=∠DOC=72°.
故答案为:72°.
18.解:如图,连接OA,OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB,
∴△AOB是等腰直角三角形,
∴OA=OB=AB=3,
即⊙O的半径是3,
故答案为:3.
19.解:过G作GM⊥AC于M,连接AG,如图所示:
∵GO⊥AB,
∴OA=OB,
∵G(0,2),
∴OG=2,
在Rt△AGO中,∵AG=4,OG=2,
∴AG=2OG,OA==2,
∴∠GAO=30°,AB=2AO=4,
∴∠AGO=60°,
∵GC=GA=4,
∴∠GCA=∠GAC,
∵∠AGO=∠GCA+∠GAC,
∴∠GCA=∠GAC=30°,
∴AC=2OA=4,MG=CG=2,
∵∠AFC=90°,
∴点F在以AC为直径的⊙M上,
当点F在MG的延长线上时,FG的长最小,最小值=FM﹣MG=2﹣2,
故答案为:2﹣2.
20.解:∵∠BOD=32°,
∴∠AOC=∠BOD=32°,
∵=,
∴∠AOE=∠AOC=32°,
∴∠COE=∠AOC+∠AOE=32°+32°=64°,
故答案为:64.
三.解答题
21.(1)证明:∵PG平分∠EPF,
∴∠DPO=∠APO,
∵OA∥PE,
∴∠DPO=∠AOP,
∴∠APO=∠AOP,
∴AP=AO;
(2)解:过O点作OH⊥AB于H,如图,则AH=BH=AB=4,
在Rt△AOH中,∵OA=5,AH=4,
∴OH==3,
∵AP=AO=5,
∴PH=PA+AH=9,
在Rt△POH中,OP==3.
22.解:(1)如图1,连接BF,OC,
∵AB是⊙O的直径,
∴∠AFB=90°,即BF⊥AD,
∵CE是⊙O的切线,OC是⊙O的半径,
∴OC⊥CE,
∵点C为劣弧的中点,
∴OC⊥BF,
∴BF∥CE,
∴CE⊥AD;
(2)如图2,连接OF,CF,
∵OA=OC,∠BAC=30°,
∴∠BOC=60°,
∵点C为劣弧的中点,
∴=,
∴∠FOC=∠BOC=60°,
∵OF=OC,
∴∠OCF=∠COB,
∴CF∥AB,
∴S△ACF=S△COF,
∴阴影部分的面积=S扇形COF,
∵AB=4,
∴FO=OC=OB=2,
∴S扇形FOC==π,
即阴影部分的面积为:π.
23.解:(1)∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB,且∠P=60°,
∴△PAB是等边三角形;
(2)∵△PAB是等边三角形;
∴PB=AB=2cm,∠PBA=60°,
∵BC是直径,PB是⊙O切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC==,
∴AC=2×=cm.
24.解:到点A的距离小于2cm,且到点B的距离不小于2cm的所有点的集合如图所示:
25.证明:∵=,
∴∠AOC=∠BOC,
∵CD⊥OA,CE⊥OB,
∴CD=CE.
26.(1)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABD=25°,
∴∠DAB=65°,∠DOA=50°,
∵OD⊥AC,
∴∠EAF=40°,
∴∠DAC=65°﹣40°=25°;
(2)证明:∵DE⊥AB于点E,
∴∠DEO=90°,
∵∠DOA=50°,
∴∠EDO=40°,
∵AO=DO,
∴∠OAD=∠ADO=65°,
∴∠ADE=65°﹣40°=25°,
∵∠DAC=25°,
∴AF=DF.
27.解:(1)如图,连接EC,
∵AD⊥BC于点D,AD=BD,
∴∠ABD=∠BAD=45°,
∴∠AEC=∠ABD=45°,
∵AE是⊙O的直径,
∴∠ACE=90°,
∵AE=4,
∴AC=AE?sin45°=4×=2;
(2)证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ABE=∠ADC,
∵∠AEB=∠ACB,
∴△ABE∽△ADC,
∴BE:DC=AE:AC=4:2=,
∴BE=DC.
