沪科版八年级上册数学 12.2 一次函数图像及性质学案(无答案)
文档属性
| 名称 | 沪科版八年级上册数学 12.2 一次函数图像及性质学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 145.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 00:00:00 | ||
图片预览


文档简介
沪科版八年级上册数学一次函数
一次函数图像及性质
要点提示
知识点一:一次函数的定义
一般地,形如(,是常数,)的函数,叫做一次函数,当时,即,为正比例函数.
⑴一次函数的解析式的形式是,要判断一个函数是否是一次函数,就是判断是否能化成以上形式.
⑵当,时,仍是一次函数.
⑶当,时,它不是一次函数.
⑷正比例函数是一次函数的特例,一次函数包括正比例函数.
知识点二:一次函数的图象及其画法
⑴一次函数(,,为常数)的图象是一条直线.
⑵由于两点确定一条直线,所以在平面直角坐标系内画一次函数的图象时,只要先描出两个点,再连成直线即可.
①如果这个函数是正比例函数,通常取,两点;
②如果这个函数是一般的一次函数(),通常取,,即直线与两坐标轴的交点.
⑶由函数图象的意义知,满足函数关系式的点在其对应的图象上,这个图象就是一条直线,反之,直线上的点的坐标满足,也就是说,直线与是一一对应的,所以通常把一次函数的图象叫做直线:,有时直接称为直线.
知识点三:一次函数的性质
⑴当时,一次函数的图象从左到右上升,随的增大而增大;
⑵当时,一次函数的图象从左到右下降,随的增大而减小.
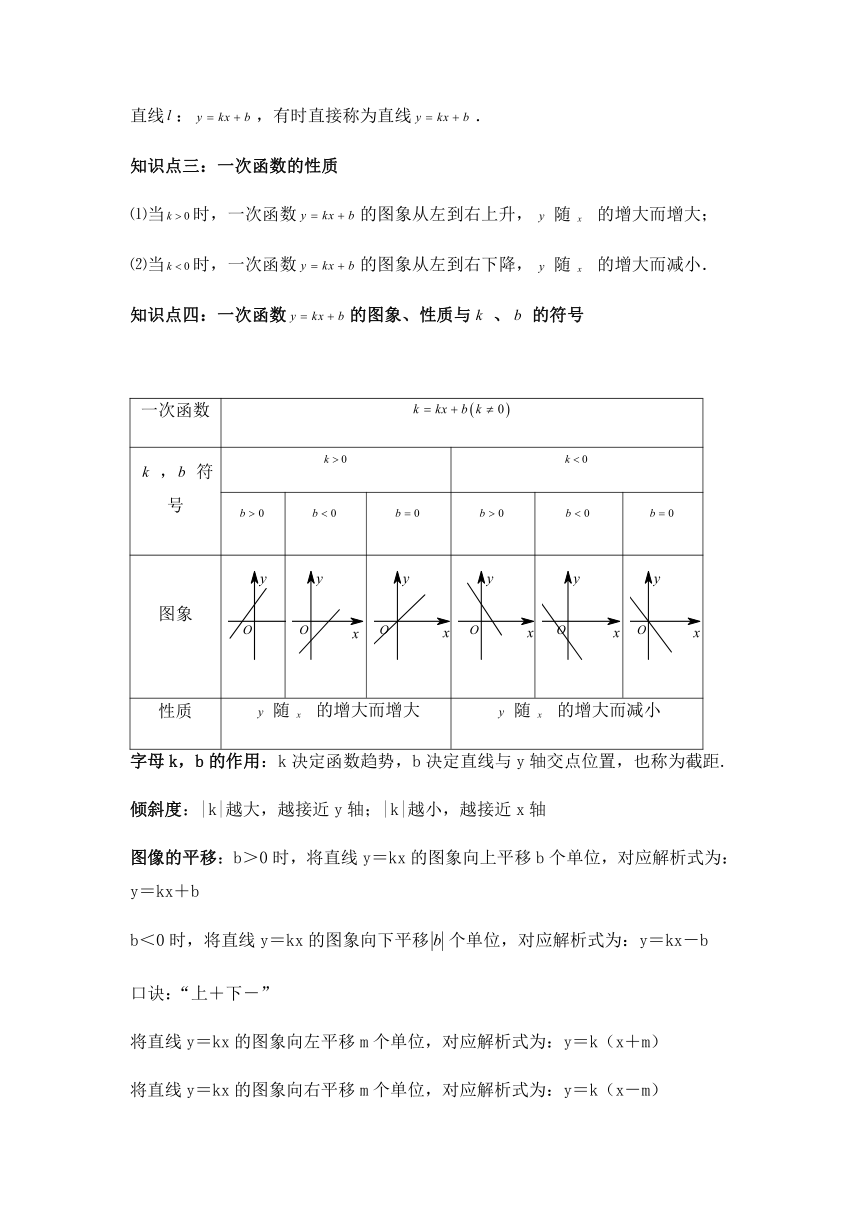
知识点四:一次函数的图象、性质与、的符号
一次函数
,符号
图象
性质
随的增大而增大
随的增大而减小
字母k,b的作用:k决定函数趋势,b决定直线与y轴交点位置,也称为截距.
倾斜度:|k|越大,越接近y轴;|k|越小,越接近x轴
图像的平移:b>0时,将直线y=kx的图象向上平移b个单位,对应解析式为:y=kx+b
b<0时,将直线y=kx的图象向下平移个单位,对应解析式为:y=kx-b
口诀:“上+下-”
将直线y=kx的图象向左平移m个单位,对应解析式为:y=k(x+m)
将直线y=kx的图象向右平移m个单位,对应解析式为:y=k(x-m)
口诀:“左+右-”
知识点五:用待定系数法求一次函数的解析式
⑴定义:先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
⑵用待定系数法求函数解析式的一般步骤:
①根据已知条件写出含有待定系数的解析式;
②将的几对值,或图象上的几个点的坐标代入上述的解析式中,得到以待定系数为未知数的方程或方程组;
③解方程(组),得到待定系数的值;
④将求出的待定系数代回所求的函数解析式中,得到所求的函数解析式.
典例分析
1.下列关于x的函数中,是一次函数的是(
)
2.如果直线y=kx+b经过一、二、四象限,那么有()
A.k>0,b>0
B.k>0,b<0
C.k
<
0,b<0
D.k
<0,b>0
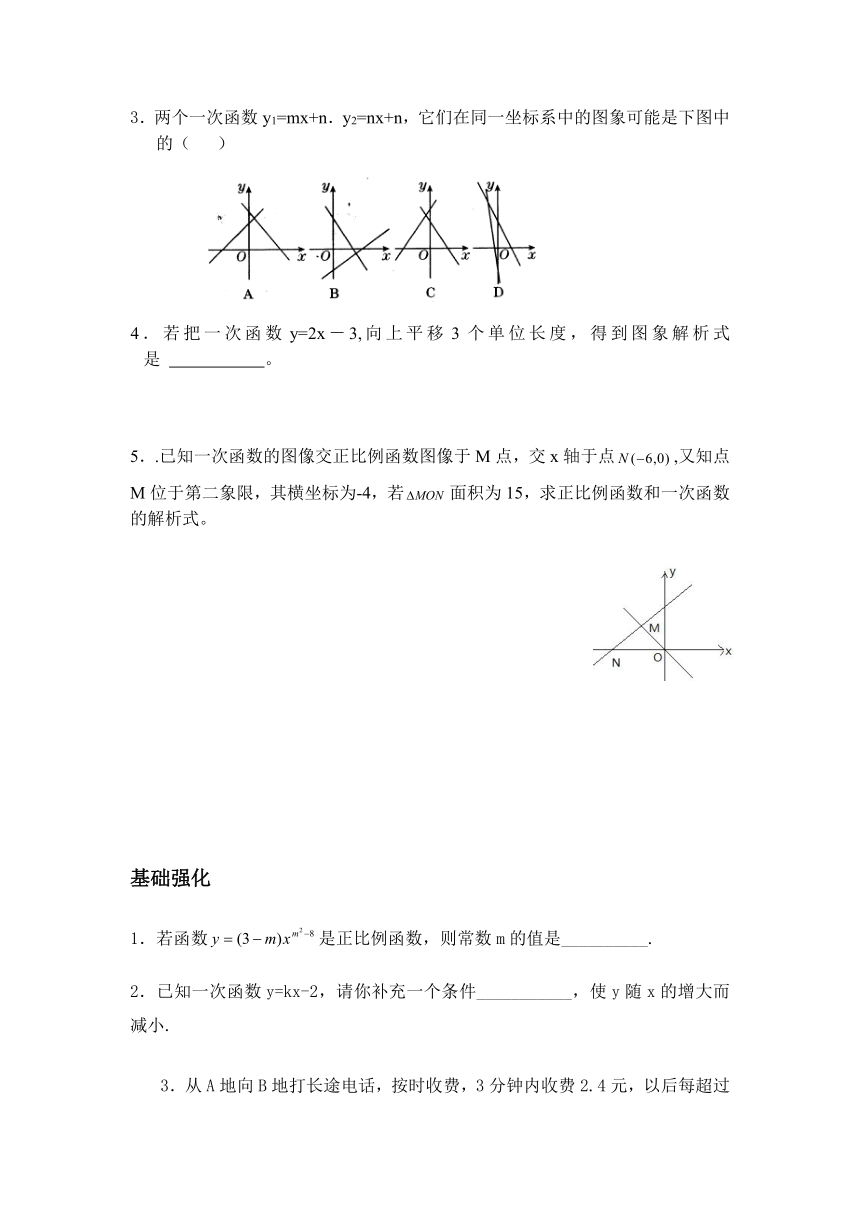
3.两个一次函数y1=mx+n.y2=nx+n,它们在同一坐标系中的图象可能是下图中的(
)
4.若把一次函数y=2x-3,向上平移3个单位长度,得到图象解析式是
。
5..已知一次函数的图像交正比例函数图像于M点,交x轴于点,又知点M位于第二象限,其横坐标为-4,若面积为15,求正比例函数和一次函数的解析式。
基础强化
1.若函数是正比例函数,则常数m的值是__________.
2.已知一次函数y=kx-2,请你补充一个条件___________,使y随x的增大而减小.
3.从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t≥3),则需付电话费y(元)与t(分钟)之间的函数关系式是_______.
4.已知一次函数y=-3x+1的图象经过点(a,1)和点(-2,b),则a=________,b=______.
5.若点A(2,
4)在函数y=k
x-2的图象上,则下列各点在此函数图象上的是(
)
A.(0,-2)
B.(1.5,0)
C.(8,
20)
D.(0.5,0.5)。
6.函数y=k(x-k)
(k<0)
的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.如果直线y=2x+m与两坐标轴围成的三角形面积等于m,则m的值是(
)
A.±3
B.3
C.±4
D.4
8.下列函数中,y是x的正比例函数的是(
)
A.y=2x-1
B.y=
2x
C.y=2x+1
D.y=-2x+1
9.已知一次函数图象经过(3,5)和(-4,-9)两点,
(1)求此一次函数解析式;
(2)若点(a,2)在函数图象上,求a的值.
10.根据下列条件,确定函数关系式:
(1)y与x成正比,且当x=9时,y=16;
(2)y=kx+b的图象经过点(3,2)和点(-2,1).
能力提高
1.已知是整数,且一次函数的图象不过第二象限,则为
。
2.已知函数y=(k-1)x+k2-1,当k_______时,它是一次函数,当k=_______时,它是正比例函数。
3.要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足
,
.
4.如图,两直线和在同一坐标系内图象的位置可能是(
)
5.已知一次函数求:
(1)m为何值时,y随x的增大而减小;
(2)m,n分别为何值时,函数的图象与y轴的交点在x轴的下方?
(3)m,n分别为何值时,函数的图象经过原点?
(4)当时,设此一次函数与x轴交于A,与y轴交于B,试求面积。
真题演练
1.已知直线经过点和,则的值为(
).
A.
B.
C.
D.
2.一次函数y=3x-2的函数值y随自变量x值的增大而_____________(填“增大”或“减小”)
3.已知函数的图象如图象如图,则的图象可能是(
)
4.一次函数的图象过点(-l
,
0
)
,且函数值随着自变量的增大而减小,写出一个符合这个条件的一次函数解析式
。
一次函数图像及性质
要点提示
知识点一:一次函数的定义
一般地,形如(,是常数,)的函数,叫做一次函数,当时,即,为正比例函数.
⑴一次函数的解析式的形式是,要判断一个函数是否是一次函数,就是判断是否能化成以上形式.
⑵当,时,仍是一次函数.
⑶当,时,它不是一次函数.
⑷正比例函数是一次函数的特例,一次函数包括正比例函数.
知识点二:一次函数的图象及其画法
⑴一次函数(,,为常数)的图象是一条直线.
⑵由于两点确定一条直线,所以在平面直角坐标系内画一次函数的图象时,只要先描出两个点,再连成直线即可.
①如果这个函数是正比例函数,通常取,两点;
②如果这个函数是一般的一次函数(),通常取,,即直线与两坐标轴的交点.
⑶由函数图象的意义知,满足函数关系式的点在其对应的图象上,这个图象就是一条直线,反之,直线上的点的坐标满足,也就是说,直线与是一一对应的,所以通常把一次函数的图象叫做直线:,有时直接称为直线.
知识点三:一次函数的性质
⑴当时,一次函数的图象从左到右上升,随的增大而增大;
⑵当时,一次函数的图象从左到右下降,随的增大而减小.
知识点四:一次函数的图象、性质与、的符号
一次函数
,符号
图象
性质
随的增大而增大
随的增大而减小
字母k,b的作用:k决定函数趋势,b决定直线与y轴交点位置,也称为截距.
倾斜度:|k|越大,越接近y轴;|k|越小,越接近x轴
图像的平移:b>0时,将直线y=kx的图象向上平移b个单位,对应解析式为:y=kx+b
b<0时,将直线y=kx的图象向下平移个单位,对应解析式为:y=kx-b
口诀:“上+下-”
将直线y=kx的图象向左平移m个单位,对应解析式为:y=k(x+m)
将直线y=kx的图象向右平移m个单位,对应解析式为:y=k(x-m)
口诀:“左+右-”
知识点五:用待定系数法求一次函数的解析式
⑴定义:先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法,叫做待定系数法.
⑵用待定系数法求函数解析式的一般步骤:
①根据已知条件写出含有待定系数的解析式;
②将的几对值,或图象上的几个点的坐标代入上述的解析式中,得到以待定系数为未知数的方程或方程组;
③解方程(组),得到待定系数的值;
④将求出的待定系数代回所求的函数解析式中,得到所求的函数解析式.
典例分析
1.下列关于x的函数中,是一次函数的是(
)
2.如果直线y=kx+b经过一、二、四象限,那么有()
A.k>0,b>0
B.k>0,b<0
C.k
<
0,b<0
D.k
<0,b>0
3.两个一次函数y1=mx+n.y2=nx+n,它们在同一坐标系中的图象可能是下图中的(
)
4.若把一次函数y=2x-3,向上平移3个单位长度,得到图象解析式是
。
5..已知一次函数的图像交正比例函数图像于M点,交x轴于点,又知点M位于第二象限,其横坐标为-4,若面积为15,求正比例函数和一次函数的解析式。
基础强化
1.若函数是正比例函数,则常数m的值是__________.
2.已知一次函数y=kx-2,请你补充一个条件___________,使y随x的增大而减小.
3.从A地向B地打长途电话,按时收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若通话t分钟(t≥3),则需付电话费y(元)与t(分钟)之间的函数关系式是_______.
4.已知一次函数y=-3x+1的图象经过点(a,1)和点(-2,b),则a=________,b=______.
5.若点A(2,
4)在函数y=k
x-2的图象上,则下列各点在此函数图象上的是(
)
A.(0,-2)
B.(1.5,0)
C.(8,
20)
D.(0.5,0.5)。
6.函数y=k(x-k)
(k<0)
的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.如果直线y=2x+m与两坐标轴围成的三角形面积等于m,则m的值是(
)
A.±3
B.3
C.±4
D.4
8.下列函数中,y是x的正比例函数的是(
)
A.y=2x-1
B.y=
2x
C.y=2x+1
D.y=-2x+1
9.已知一次函数图象经过(3,5)和(-4,-9)两点,
(1)求此一次函数解析式;
(2)若点(a,2)在函数图象上,求a的值.
10.根据下列条件,确定函数关系式:
(1)y与x成正比,且当x=9时,y=16;
(2)y=kx+b的图象经过点(3,2)和点(-2,1).
能力提高
1.已知是整数,且一次函数的图象不过第二象限,则为
。
2.已知函数y=(k-1)x+k2-1,当k_______时,它是一次函数,当k=_______时,它是正比例函数。
3.要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足
,
.
4.如图,两直线和在同一坐标系内图象的位置可能是(
)
5.已知一次函数求:
(1)m为何值时,y随x的增大而减小;
(2)m,n分别为何值时,函数的图象与y轴的交点在x轴的下方?
(3)m,n分别为何值时,函数的图象经过原点?
(4)当时,设此一次函数与x轴交于A,与y轴交于B,试求面积。
真题演练
1.已知直线经过点和,则的值为(
).
A.
B.
C.
D.
2.一次函数y=3x-2的函数值y随自变量x值的增大而_____________(填“增大”或“减小”)
3.已知函数的图象如图象如图,则的图象可能是(
)
4.一次函数的图象过点(-l
,
0
)
,且函数值随着自变量的增大而减小,写出一个符合这个条件的一次函数解析式
。
