2020-2021学年华东师大新版九年级下册数学《第27章 圆》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年华东师大新版九年级下册数学《第27章 圆》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 424.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-03 22:25:01 | ||
图片预览




文档简介
2020-2021学年华东师大新版九年级下册数学《第27章
圆》单元测试卷
一.选择题
1.下列说法:
①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.
正确的说法有( )
A.1个
B.2个
C.3个
D.4个
2.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OB=3:5,连接DO,则DE的长为( )
A.3
B.4
C.6
D.8
3.已知⊙O的半径r,圆心O到直线的距离为d,当d<r时,直线与⊙O的位置关系是( )
A.相交
B.相切
C.相离
D.以上都不对
4.如图,五边形ABCDE是⊙O的内接正五边形,则正五边形中心角∠COD的度数是( )
A.60°
B.36°
C.76°
D.72°
5.如图,点A,B,C在⊙O上,∠ACB=38°,则∠AOB等于( )
A.52°
B.68°
C.76°
D.86°
6.如图,圆内接四边形ABCD的对角线AC,BD把它的4个内分角成8个角,用下列关于角的等量关系不一定成立的是( )
A.∠1=∠4
B.∠1+∠2+∠3+∠5=180°
C.∠4=∠7
D.∠ADC=∠2+∠5
7.已知⊙O的半径是4cm,点P到圆心O的距离为4.5cm,则点P与⊙O的位置关系是( )
A.⊙O内
B.⊙O上
C.⊙O外
D.以上都有可能
8.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯长一尺,问径如何?”这段话的意思是:如图,现有圆形木材,埋在墙壁里,不知木材大小,用锯子将它锯下来,深度CD为1寸,锯长AB为1尺(10寸),问圆材直径几寸?则该问题中圆的直径为( )
A.22寸
B.24寸
C.26寸
D.28寸
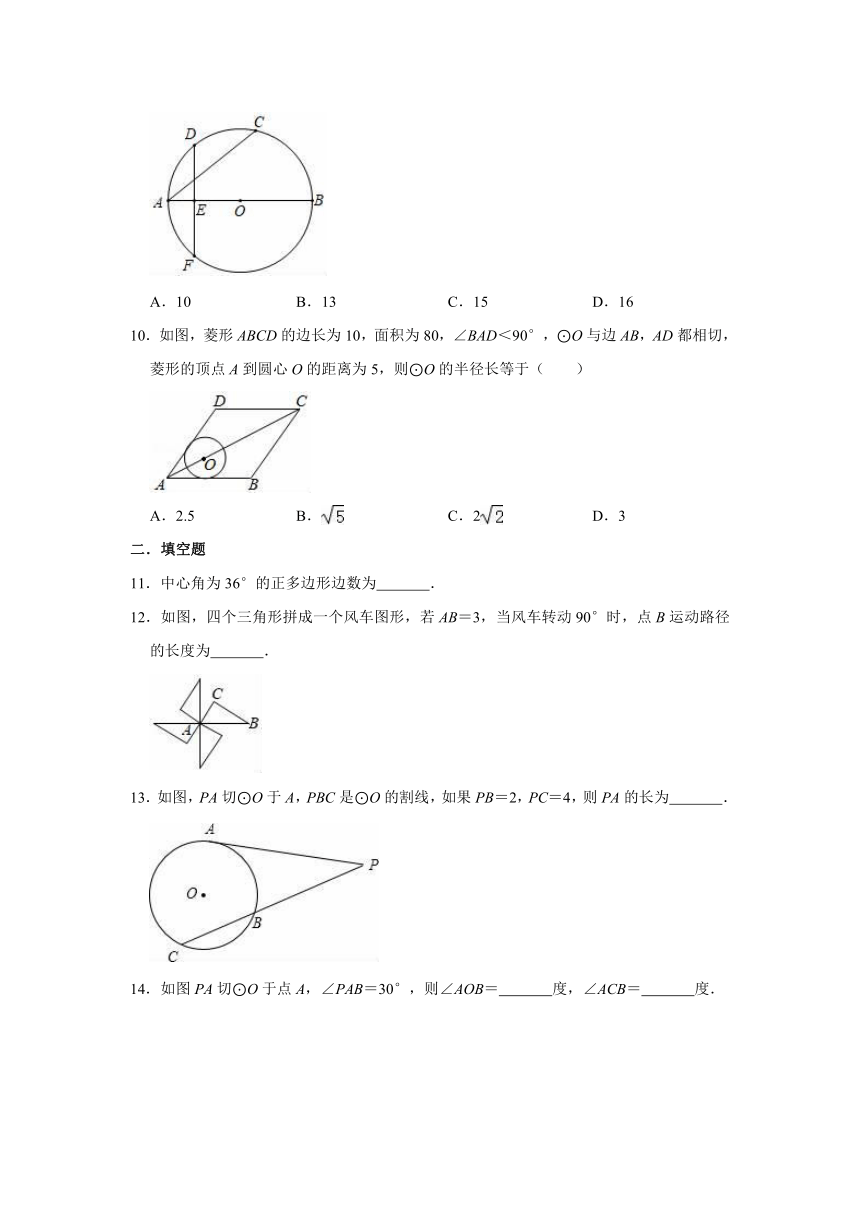
9.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AC=12,AE=3,则⊙O的直径长为( )
A.10
B.13
C.15
D.16
10.如图,菱形ABCD的边长为10,面积为80,∠BAD<90°,⊙O与边AB,AD都相切,菱形的顶点A到圆心O的距离为5,则⊙O的半径长等于( )
A.2.5
B.
C.2
D.3
二.填空题
11.中心角为36°的正多边形边数为
.
12.如图,四个三角形拼成一个风车图形,若AB=3,当风车转动90°时,点B运动路径的长度为
.
13.如图,PA切⊙O于A,PBC是⊙O的割线,如果PB=2,PC=4,则PA的长为
.
14.如图PA切⊙O于点A,∠PAB=30°,则∠AOB=
度,∠ACB=
度.
15.如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=,以O为圆心,OC为半径作,交OB于E点,阴影部分的面积为
.
16.已知△ACB中,∠ACB=90°,以AB为直径作⊙O,则点C在⊙O
(填内、上或外).
17.已知圆锥的侧面展开的扇形面积是24π,扇形的圆心角是60°,则这个圆锥的底面圆的半径是
.
18.已知三角形三边分别为3、4、5,则该三角形内心与外心之间的距离为
.
19.如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=AC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是
.
20.如图所示,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,若以点C为圆心,r为半径的圆与边AB所在直线有公共点,则r的取值范围为
.
三.解答题
21.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=6,求CD的长.
22.如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)求弦AB的长;
(2)当∠D=20°时,求∠BOD的度数.
23.我们知道,到线段两端距离相等的点在线段的垂直平分线上.由此,我们可以引入如下新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
(1)如图1,点P在线段BC上,∠ABP=∠APD=∠PCD=90°,BP=CD.求证:点P是△APD的准外心;
(2)如图2,在Rt△ABC中,∠BAC=90°,BC=5,AB=3,△ABC的准外心P在△ABC的直角边上,试求AP的长.
24.如图,在平面直角坐标系中,⊙O的半径为1,则直线y=﹣2x+与⊙O的位置关系怎样?
25.如图,AB为⊙O的直径,PQ切⊙O于E,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=EC=4,求⊙O的半径.
26.在扇形OAB中,C是弧AB上一点,延长AC到D,且∠BCD=75°.
(1)求∠AOB的度数;
(2)扇形OAB是某圆锥的侧面展开图,若OA=12,求该圆锥的底面半径.
27.如图,已知⊙O是边长为6的等边△ABC的外接圆,点D,E分别是BC,AC上两点,且BD=CE,连接AD,BE相交于点P,延长线段BE交⊙O于点F,连接CF.
(1)求证:AD∥FC;
(2)连接PC,当△PEC为直角三角形时,求tan∠ACF的值.
参考答案与试题解析
一.选择题
1.解:①直径是弦,正确,符合题意;
②弦不一定是直径,错误,不符合题意;
③半径相等的两个半圆是等弧,正确,符合题意;
④能够完全重合的两条弧是等弧,故原命题错误,不符合题意;
⑤半圆是弧,但弧不一定是半圆,正确,符合题意,
正确的有3个,
故选:C.
2.解:∵AB=10,OC:OB=3:5,
∴OC=3,
在Rt△OCD中,CD===4,
∵DE⊥AB,
∴DE=2CD=8,
故选:D.
3.解:已知⊙O的半径r,圆心O到直线的距离为d,当d<r时,直线与⊙O的位置关系是相交,
故选:A.
4.解:∵五边形ABCDE是⊙O的内接正五边形,
∴五边形ABCDE的中心角∠COD的度数为=72°,
故选:D.
5.解:∵∠ACB=38°,
∴∠AOB=2∠ACB=76°.
故选:C.
6.解:∵∠1,∠4所对的弧都是弧CD,
∴∠1=∠4,
∵∠2,∠7所对的弧都是弧BC,
∴∠2=∠7,
∵∠5,∠8所对的弧都是弧AB.
∴∠5=∠8,
∵∠1+∠2+∠3+∠8=180°,∠ADC=∠8+∠7,
∴∠1+∠2+∠3+∠5=180°,∠ADC=∠2+∠5,
故A,B,D都正确,
∵和不一定相等,
∴BC与DC不一定相等,
∴∠4与∠7不一定相等,
故C错误,
故选:C.
7.解:∵OP=4.5>4,
∴点P与⊙O的位置关系是点在圆外.
故选:C.
8.解:设圆材的圆心为O,延长CD,交⊙O于点E,连接OA,如图所示:
由题意知:CE过点O,且OC⊥AB,
则AD=BD=AB=5,
设圆形木材半径为r,
则OD=r﹣1,OA=r,
∵OA2=OD2+AD2,
∴r2=(r﹣1)2+52,
解得:r=13,
即⊙O的半径为13寸,
∴⊙O的直径为26寸,
故选:C.
9.解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,=,
∵点D是弧AC的中点,
∴=,
∴=,
∴AC=DF=12,
∴EF=DF=6,设OA=OF=x,
在Rt△OEF中,则有x2=62+(x﹣3)2,
解得x=,
∴AB=2x=15,
故选:C.
10.解:如图,连接BD交AC于点O′,作BF⊥CD于F,过点O作OE⊥AB,垂足为E,
∵菱形ABCD的边长为10,面积为80,
∴CD?BF=80,
∴BF=8,
∴FC===6,
∴DF=CD﹣FC=10﹣6=4,
∴BD===4,
∴O′D=O′B=BD=2,
∵∠AEO=∠AO′B=90°,∠OAE=∠BAO′,
∴△AOE∽△ABO′,
∴=,
即:=,
∴OE=,
故选:B.
二.填空题
11.解:由题意可得:
∵360°÷36°=10,
∴它的边数是10.
故答案为10.
12.解:∵AB=3,风车转动90°,
∴点B运动路径的长度==π,
故答案为:π.
13.解:∵PA切⊙O于A,PBC是⊙O的割线,PB=2,PC=4,
∴PA2=PB×PC,
∴PA==2.
故答案为:2.
14.解:由弦切角定理知,∠C=∠BAP=30°;
由圆周角定理知,∠AOB=2∠C=60°.
15.解:由题意可得,
OD=2OC,∠OCD=90°,
∵CD=,
∴OC=1,OD=2,
∴∠ODC=30°,
∴∠COD=60°,
∴∠DOB=30°,
∴阴影部分的面积是:
+﹣=,
故答案为:
.
16.解:∵AB为直径作⊙O,
∴OA=OB,
∵O是直角三角形斜边AB的中点,
∴OA=OB=OC,
∴点C在⊙O上,
故答案为:上.
17.解:设扇形的半径为r,圆锥的底面半径为R.
由题意,=24π,
解得r=12或﹣12(舍弃),
∵扇形的弧长=圆锥底面圆的周长,
∴=2?π?R,
∴R=2,
故答案为:2.
18.解:∵三角形三边分别为3、4、5,
∴32+42=52,
∴三角形是直角三角形,
如图,设Rt△ABC,∠C=90°,AC=3,BC=4,AB=5,
设Rt△ABC的内切圆的半径为r,则OD=OE=r,
∵∠C=90°,
∴CE=CD=r,AE=AN=3﹣r,BD=BN=4﹣r,
∴4﹣r+3﹣r=5,
解得r=1,
∴AN=2,
在Rt△OMN中,MN=AM﹣AN=,
∴OM=.
则该三角形内心与外心之间的距离为.
故答案为:.
19.解:连接AD,
∵D为BC中点,点O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥AC,①正确;
∵AB是⊙O的直径,
∴∠ADB=90°=∠ADC,
即AD⊥BC,又BD=CD,
∴△ABC为等腰三角形,
∴∠B=∠C,②正确;
∵DE⊥AC,且DO∥AC,
∴OD⊥DE,
∵OD是半径,
∴DE是⊙O的切线,∴④正确;
∴∠ODA+∠EDA=90°,
∵∠ADB=∠ADO+∠ODB=90°,
∴∠EDA=∠ODB,
∵OD=OB,
∴∠B=∠ODB,
∴∠EDA=∠B,∴⑤正确;
∵D为BC中点,AD⊥BC,
∴AC=AB,
∵OA=OB=AB,
∴OA=AC,
∴③正确,
故答案为:①②③④⑤.
20.解:如图,作CH⊥AB于H.
在Rt△ABC中,∵∠ACB=90°,BC=8,AC=6,
∴AB===10,
∵S△ABC=?AC?BC=?AB?CH,
∴CH=,
∵以点C为圆心,r为半径的圆与边AB所在直线有公共点,
∴r≥,
故答案为r≥.
三.解答题
21.(1)证明:连接AC,如图所示:
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,
即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=6,
∴OC=AB=3,
又∵BE=OE,
∴OE=,
∴CE===,
∴CD=2CE=3.
22.解:(1)过点O作OE⊥AB于E,如图:
则AE=BE=AB,∠OEB=90°,
∵OB=2,∠B=30°,
∴OE=OB=1,BE=OE=,
∴AB=2BE=2;
(2)连接OA,如图:
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D,
又∵∠B=30°,∠D=20°,
∴∠DAB=50°,
∴∠BOD=2∠DAB=100°.
23.(1)证明:∵∠ABP=∠APD=∠PCD=90°,
∴∠APB+∠PAB=90°,∠APB+∠DPC=90°,
∴∠PAB=∠DPC,
在△ABP和△PCD中,
,
∴△ABP≌△PCD(AAS),
∴AP=PD,
∴点P是△APD的准外心;
(2)解:∵∠BAC=90°,BC=5,AB=3,
∴AC==4,
当P点在AB上,PA=PB,则AP=AB=;
当P点在AC上,PA=PC,则AP=AC=2,
当P点在AC上,PB=PC,如图2,
设AP=t,则PC=PB=4﹣x,
在Rt△ABP中,32+t2=(4﹣t)2,解得t=,
即此时AP=,
综上所述,AP的长为或2或.
24.解:如图所示,过O作OC⊥直线AB,垂足为C,
在直线y=﹣2x+中,令x=0,解得:y=;令y=0,解得:x=,
∴A(,0),B(0,),即OA=,OB=,
在Rt△AOB中,根据勾股定理得:AB===,
又S△AOB=AB?OC=OA?OB,
∴OC===1,又圆O的半径为1,
则直线y=﹣2x+与圆O的位置关系是相切.
25.(1)证明:连接OE,
∴OA=OE,
∴∠OEA=∠OAE.
∵PQ切⊙O于E,
∴OE⊥PQ.
∵AC⊥PQ,
∴OE∥AC.
∴∠OEA=∠EAC,
∴∠OAE=∠EAC,
∴AE平分∠BAC.
(2)解:过点O作OM⊥AC于M,
∴AM=MD==2;
又∠OEC=∠ACE=∠OMC=90°,
∴四边形OECM为矩形,
∴OM=EC=4,
在Rt△AOM中,OA===2;
即⊙O的半径为2.
26.解:(1)作出所对的圆周角∠APB,
∵∠APB+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠APB=∠BCD=75°,
∴∠AOB=2∠APB=150°;
(2)设该圆锥的底面半径为r,
根据题意得2πr=,解得r=5,
∴该圆锥的底面半径为5.
27.解:(1)∵△ABC为等边三角形,
∴AB=BC,
∴∠ABD=∠∠BCE=60°,
∵BD=CE,
∴△ABD≌△BCE(SAS),
∴∠BDA=∠CEB,
∵∠CEB=∠F+∠FCE,
∵∠F=∠BAC=∠BCA=60°,
∴∠CEB=∠BCA+∠FCE=∠BCF,
∴∠BDA=∠BCF,
∴AD∥CF;
(2)如图,连接PC,
当△PEC为直角三角形时,
∠PEC=90°,
∵∠PEC=∠F+∠ACF,
∵∠F=60°,
∴∠ACF=30°,
∴tan∠ACF=.
圆》单元测试卷
一.选择题
1.下列说法:
①直径是弦;②弦是直径;③半径相等的两个半圆是等弧;④长度相等的两条弧是等弧;⑤半圆是弧,但弧不一定是半圆.
正确的说法有( )
A.1个
B.2个
C.3个
D.4个
2.如图,在⊙O中,直径AB=10,弦DE⊥AB于点C,若OC:OB=3:5,连接DO,则DE的长为( )
A.3
B.4
C.6
D.8
3.已知⊙O的半径r,圆心O到直线的距离为d,当d<r时,直线与⊙O的位置关系是( )
A.相交
B.相切
C.相离
D.以上都不对
4.如图,五边形ABCDE是⊙O的内接正五边形,则正五边形中心角∠COD的度数是( )
A.60°
B.36°
C.76°
D.72°
5.如图,点A,B,C在⊙O上,∠ACB=38°,则∠AOB等于( )
A.52°
B.68°
C.76°
D.86°
6.如图,圆内接四边形ABCD的对角线AC,BD把它的4个内分角成8个角,用下列关于角的等量关系不一定成立的是( )
A.∠1=∠4
B.∠1+∠2+∠3+∠5=180°
C.∠4=∠7
D.∠ADC=∠2+∠5
7.已知⊙O的半径是4cm,点P到圆心O的距离为4.5cm,则点P与⊙O的位置关系是( )
A.⊙O内
B.⊙O上
C.⊙O外
D.以上都有可能
8.“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯长一尺,问径如何?”这段话的意思是:如图,现有圆形木材,埋在墙壁里,不知木材大小,用锯子将它锯下来,深度CD为1寸,锯长AB为1尺(10寸),问圆材直径几寸?则该问题中圆的直径为( )
A.22寸
B.24寸
C.26寸
D.28寸
9.如图,AB为⊙O的直径,点D是弧AC的中点,过点D作DE⊥AB于点E,延长DE交⊙O于点F,若AC=12,AE=3,则⊙O的直径长为( )
A.10
B.13
C.15
D.16
10.如图,菱形ABCD的边长为10,面积为80,∠BAD<90°,⊙O与边AB,AD都相切,菱形的顶点A到圆心O的距离为5,则⊙O的半径长等于( )
A.2.5
B.
C.2
D.3
二.填空题
11.中心角为36°的正多边形边数为
.
12.如图,四个三角形拼成一个风车图形,若AB=3,当风车转动90°时,点B运动路径的长度为
.
13.如图,PA切⊙O于A,PBC是⊙O的割线,如果PB=2,PC=4,则PA的长为
.
14.如图PA切⊙O于点A,∠PAB=30°,则∠AOB=
度,∠ACB=
度.
15.如图,在⊙O中,半径OA⊥OB,过OA的中点C作FD∥OB交⊙O于D、F两点,且CD=,以O为圆心,OC为半径作,交OB于E点,阴影部分的面积为
.
16.已知△ACB中,∠ACB=90°,以AB为直径作⊙O,则点C在⊙O
(填内、上或外).
17.已知圆锥的侧面展开的扇形面积是24π,扇形的圆心角是60°,则这个圆锥的底面圆的半径是
.
18.已知三角形三边分别为3、4、5,则该三角形内心与外心之间的距离为
.
19.如图,以△ABC的边AB为直径的⊙O恰好过BC的中点D,过点D作DE⊥AC于E,连结OD,则下列结论中:①OD∥AC;②∠B=∠C;③2OA=AC;④DE是⊙O的切线;⑤∠EDA=∠B,正确的序号是
.
20.如图所示,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,若以点C为圆心,r为半径的圆与边AB所在直线有公共点,则r的取值范围为
.
三.解答题
21.如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
(1)请证明:E是OB的中点;
(2)若AB=6,求CD的长.
22.如图,已知AB是⊙O的弦,OB=2,∠B=30°,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长CO交⊙O于点D,连接AD.
(1)求弦AB的长;
(2)当∠D=20°时,求∠BOD的度数.
23.我们知道,到线段两端距离相等的点在线段的垂直平分线上.由此,我们可以引入如下新定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
(1)如图1,点P在线段BC上,∠ABP=∠APD=∠PCD=90°,BP=CD.求证:点P是△APD的准外心;
(2)如图2,在Rt△ABC中,∠BAC=90°,BC=5,AB=3,△ABC的准外心P在△ABC的直角边上,试求AP的长.
24.如图,在平面直角坐标系中,⊙O的半径为1,则直线y=﹣2x+与⊙O的位置关系怎样?
25.如图,AB为⊙O的直径,PQ切⊙O于E,AC⊥PQ于C,交⊙O于D.
(1)求证:AE平分∠BAC;
(2)若AD=EC=4,求⊙O的半径.
26.在扇形OAB中,C是弧AB上一点,延长AC到D,且∠BCD=75°.
(1)求∠AOB的度数;
(2)扇形OAB是某圆锥的侧面展开图,若OA=12,求该圆锥的底面半径.
27.如图,已知⊙O是边长为6的等边△ABC的外接圆,点D,E分别是BC,AC上两点,且BD=CE,连接AD,BE相交于点P,延长线段BE交⊙O于点F,连接CF.
(1)求证:AD∥FC;
(2)连接PC,当△PEC为直角三角形时,求tan∠ACF的值.
参考答案与试题解析
一.选择题
1.解:①直径是弦,正确,符合题意;
②弦不一定是直径,错误,不符合题意;
③半径相等的两个半圆是等弧,正确,符合题意;
④能够完全重合的两条弧是等弧,故原命题错误,不符合题意;
⑤半圆是弧,但弧不一定是半圆,正确,符合题意,
正确的有3个,
故选:C.
2.解:∵AB=10,OC:OB=3:5,
∴OC=3,
在Rt△OCD中,CD===4,
∵DE⊥AB,
∴DE=2CD=8,
故选:D.
3.解:已知⊙O的半径r,圆心O到直线的距离为d,当d<r时,直线与⊙O的位置关系是相交,
故选:A.
4.解:∵五边形ABCDE是⊙O的内接正五边形,
∴五边形ABCDE的中心角∠COD的度数为=72°,
故选:D.
5.解:∵∠ACB=38°,
∴∠AOB=2∠ACB=76°.
故选:C.
6.解:∵∠1,∠4所对的弧都是弧CD,
∴∠1=∠4,
∵∠2,∠7所对的弧都是弧BC,
∴∠2=∠7,
∵∠5,∠8所对的弧都是弧AB.
∴∠5=∠8,
∵∠1+∠2+∠3+∠8=180°,∠ADC=∠8+∠7,
∴∠1+∠2+∠3+∠5=180°,∠ADC=∠2+∠5,
故A,B,D都正确,
∵和不一定相等,
∴BC与DC不一定相等,
∴∠4与∠7不一定相等,
故C错误,
故选:C.
7.解:∵OP=4.5>4,
∴点P与⊙O的位置关系是点在圆外.
故选:C.
8.解:设圆材的圆心为O,延长CD,交⊙O于点E,连接OA,如图所示:
由题意知:CE过点O,且OC⊥AB,
则AD=BD=AB=5,
设圆形木材半径为r,
则OD=r﹣1,OA=r,
∵OA2=OD2+AD2,
∴r2=(r﹣1)2+52,
解得:r=13,
即⊙O的半径为13寸,
∴⊙O的直径为26寸,
故选:C.
9.解:如图,连接OF.
∵DE⊥AB,
∴DE=EF,=,
∵点D是弧AC的中点,
∴=,
∴=,
∴AC=DF=12,
∴EF=DF=6,设OA=OF=x,
在Rt△OEF中,则有x2=62+(x﹣3)2,
解得x=,
∴AB=2x=15,
故选:C.
10.解:如图,连接BD交AC于点O′,作BF⊥CD于F,过点O作OE⊥AB,垂足为E,
∵菱形ABCD的边长为10,面积为80,
∴CD?BF=80,
∴BF=8,
∴FC===6,
∴DF=CD﹣FC=10﹣6=4,
∴BD===4,
∴O′D=O′B=BD=2,
∵∠AEO=∠AO′B=90°,∠OAE=∠BAO′,
∴△AOE∽△ABO′,
∴=,
即:=,
∴OE=,
故选:B.
二.填空题
11.解:由题意可得:
∵360°÷36°=10,
∴它的边数是10.
故答案为10.
12.解:∵AB=3,风车转动90°,
∴点B运动路径的长度==π,
故答案为:π.
13.解:∵PA切⊙O于A,PBC是⊙O的割线,PB=2,PC=4,
∴PA2=PB×PC,
∴PA==2.
故答案为:2.
14.解:由弦切角定理知,∠C=∠BAP=30°;
由圆周角定理知,∠AOB=2∠C=60°.
15.解:由题意可得,
OD=2OC,∠OCD=90°,
∵CD=,
∴OC=1,OD=2,
∴∠ODC=30°,
∴∠COD=60°,
∴∠DOB=30°,
∴阴影部分的面积是:
+﹣=,
故答案为:
.
16.解:∵AB为直径作⊙O,
∴OA=OB,
∵O是直角三角形斜边AB的中点,
∴OA=OB=OC,
∴点C在⊙O上,
故答案为:上.
17.解:设扇形的半径为r,圆锥的底面半径为R.
由题意,=24π,
解得r=12或﹣12(舍弃),
∵扇形的弧长=圆锥底面圆的周长,
∴=2?π?R,
∴R=2,
故答案为:2.
18.解:∵三角形三边分别为3、4、5,
∴32+42=52,
∴三角形是直角三角形,
如图,设Rt△ABC,∠C=90°,AC=3,BC=4,AB=5,
设Rt△ABC的内切圆的半径为r,则OD=OE=r,
∵∠C=90°,
∴CE=CD=r,AE=AN=3﹣r,BD=BN=4﹣r,
∴4﹣r+3﹣r=5,
解得r=1,
∴AN=2,
在Rt△OMN中,MN=AM﹣AN=,
∴OM=.
则该三角形内心与外心之间的距离为.
故答案为:.
19.解:连接AD,
∵D为BC中点,点O为AB的中点,
∴OD为△ABC的中位线,
∴OD∥AC,①正确;
∵AB是⊙O的直径,
∴∠ADB=90°=∠ADC,
即AD⊥BC,又BD=CD,
∴△ABC为等腰三角形,
∴∠B=∠C,②正确;
∵DE⊥AC,且DO∥AC,
∴OD⊥DE,
∵OD是半径,
∴DE是⊙O的切线,∴④正确;
∴∠ODA+∠EDA=90°,
∵∠ADB=∠ADO+∠ODB=90°,
∴∠EDA=∠ODB,
∵OD=OB,
∴∠B=∠ODB,
∴∠EDA=∠B,∴⑤正确;
∵D为BC中点,AD⊥BC,
∴AC=AB,
∵OA=OB=AB,
∴OA=AC,
∴③正确,
故答案为:①②③④⑤.
20.解:如图,作CH⊥AB于H.
在Rt△ABC中,∵∠ACB=90°,BC=8,AC=6,
∴AB===10,
∵S△ABC=?AC?BC=?AB?CH,
∴CH=,
∵以点C为圆心,r为半径的圆与边AB所在直线有公共点,
∴r≥,
故答案为r≥.
三.解答题
21.(1)证明:连接AC,如图所示:
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD,
∵过圆心O的线CF⊥AD,
∴AF=DF,
即CF是AD的中垂线,
∴AC=CD,
∴AC=AD=CD.
即△ACD是等边三角形,
∴∠FCD=30°,
在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点;
(2)解:在Rt△OCE中,AB=6,
∴OC=AB=3,
又∵BE=OE,
∴OE=,
∴CE===,
∴CD=2CE=3.
22.解:(1)过点O作OE⊥AB于E,如图:
则AE=BE=AB,∠OEB=90°,
∵OB=2,∠B=30°,
∴OE=OB=1,BE=OE=,
∴AB=2BE=2;
(2)连接OA,如图:
∵OA=OB,OA=OD,
∴∠BAO=∠B,∠DAO=∠D,
∴∠DAB=∠BAO+∠DAO=∠B+∠D,
又∵∠B=30°,∠D=20°,
∴∠DAB=50°,
∴∠BOD=2∠DAB=100°.
23.(1)证明:∵∠ABP=∠APD=∠PCD=90°,
∴∠APB+∠PAB=90°,∠APB+∠DPC=90°,
∴∠PAB=∠DPC,
在△ABP和△PCD中,
,
∴△ABP≌△PCD(AAS),
∴AP=PD,
∴点P是△APD的准外心;
(2)解:∵∠BAC=90°,BC=5,AB=3,
∴AC==4,
当P点在AB上,PA=PB,则AP=AB=;
当P点在AC上,PA=PC,则AP=AC=2,
当P点在AC上,PB=PC,如图2,
设AP=t,则PC=PB=4﹣x,
在Rt△ABP中,32+t2=(4﹣t)2,解得t=,
即此时AP=,
综上所述,AP的长为或2或.
24.解:如图所示,过O作OC⊥直线AB,垂足为C,
在直线y=﹣2x+中,令x=0,解得:y=;令y=0,解得:x=,
∴A(,0),B(0,),即OA=,OB=,
在Rt△AOB中,根据勾股定理得:AB===,
又S△AOB=AB?OC=OA?OB,
∴OC===1,又圆O的半径为1,
则直线y=﹣2x+与圆O的位置关系是相切.
25.(1)证明:连接OE,
∴OA=OE,
∴∠OEA=∠OAE.
∵PQ切⊙O于E,
∴OE⊥PQ.
∵AC⊥PQ,
∴OE∥AC.
∴∠OEA=∠EAC,
∴∠OAE=∠EAC,
∴AE平分∠BAC.
(2)解:过点O作OM⊥AC于M,
∴AM=MD==2;
又∠OEC=∠ACE=∠OMC=90°,
∴四边形OECM为矩形,
∴OM=EC=4,
在Rt△AOM中,OA===2;
即⊙O的半径为2.
26.解:(1)作出所对的圆周角∠APB,
∵∠APB+∠ACB=180°,∠BCD+∠ACB=180°,
∴∠APB=∠BCD=75°,
∴∠AOB=2∠APB=150°;
(2)设该圆锥的底面半径为r,
根据题意得2πr=,解得r=5,
∴该圆锥的底面半径为5.
27.解:(1)∵△ABC为等边三角形,
∴AB=BC,
∴∠ABD=∠∠BCE=60°,
∵BD=CE,
∴△ABD≌△BCE(SAS),
∴∠BDA=∠CEB,
∵∠CEB=∠F+∠FCE,
∵∠F=∠BAC=∠BCA=60°,
∴∠CEB=∠BCA+∠FCE=∠BCF,
∴∠BDA=∠BCF,
∴AD∥CF;
(2)如图,连接PC,
当△PEC为直角三角形时,
∠PEC=90°,
∵∠PEC=∠F+∠ACF,
∵∠F=60°,
∴∠ACF=30°,
∴tan∠ACF=.
