苏科版八年级上册第三章勾股定理应用:饮马模型、最值问题(需要画出展开图)(无答案)
文档属性
| 名称 | 苏科版八年级上册第三章勾股定理应用:饮马模型、最值问题(需要画出展开图)(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 138.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-04 15:21:20 | ||
图片预览

文档简介
勾:直角三角形较短的直角边;股:直角三角形较长的直角边;弦:斜边。
1、勾股定理:
直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=c2。
2、勾股定理的逆定理:
如果三角形的三边长a,b,c有关系a2+b2=c2,那么这个三角形是直角三角形。
3、勾股数:
满足a2+b2=c2的三个正整数,称为勾股数。
若是勾股数组,则na、nb、nc也是勾股数组。
4、简单运用:
⑴勾股定理——常用于求边长、周长、面积;
理解:①已知直角三角形的两边求第三边,并能求出周长、面积。
②用于证明线段平方关系的问题。
③利用勾股定理,作出长为的线段
⑵勾股定理的逆定理——常用于判断三角形的形状;
理解:①确定最大边(不妨设为c);?
②若c2=a2+b2,则△ABC是以∠C为直角的三角形;?
若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);
?
若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)
考点:最短距离及相关问题
例1.
(2017立达期中)如图,一个高16m,底面周长8m的圆柱形水塔,现制造一个螺旋形登梯,为了减小坡度,要求登梯绕塔环绕一周半到达顶端,问登梯至少多长?
例2.(2017吴中区期中)如图,一圆柱高8
cm,底面半径为2
cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是(▲)
A.20
cm
B.10
cm
C.14
cm
D.无法确定
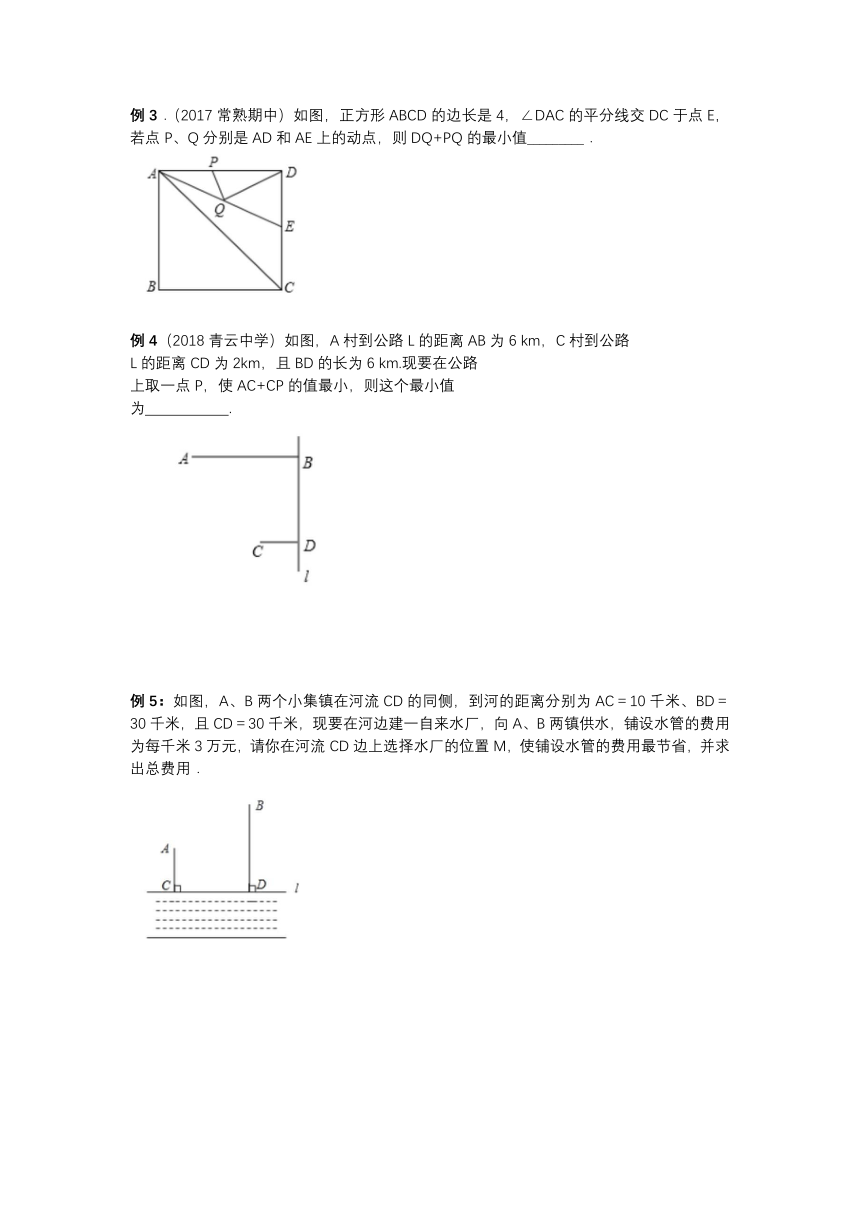
例3.(2017常熟期中)如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值_________.
例4(2018青云中学)如图,A村到公路L的距离AB为6
km,C村到公路
L的距离CD为2km,且BD的长为6
km.现要在公路
上取一点P,使AC+CP的值最小,则这个最小值
为
.
例5:如图,A、B两个小集镇在河流CD的同侧,到河的距离分别为AC=10千米、BD=30千米,且CD=30千米,现要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万元,请你在河流CD边上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用.
例6:“数学建模”
(1)模型——小马喝水问题:直线MN表示一条河流的岸,在河流同侧有A、B两地,小马从A地出发到B地,中间要在河边饮水一次,请在图①中用直尺和圆规作出使小马行走最短路程的饮水点P的位置.(作在答题纸上,保留作图痕迹,并用黑水笔将痕迹描深)
(2)运用——和最小问题:如图②,E是边长为8的正方形ABCD边BC上一点,CE=2,P是对角线BD上的一个动点,求PC+PE的最小值.
例7如图,长方体的长为15,宽为10,高为20,点B到点C的距离为5,如果一只蚂蚁要沿着长方体的表面从点A爬到点B,那么它需要爬行的最短距离是
(
)
A.5
B.25
C.15
D.35
例8如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两相对的端点,A点有一只昆虫想到B点去吃可口的食物,则昆虫沿着台阶爬到B点的最短路程是
分米。
例9.如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.
例10
如图,一个圆柱形容器的高为1.2m,底面周长为Im.在容器内壁离容器底部0.3m的点B处有一只蚊子,此时一只壁虎正好在容器外壁离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为_______m(容器厚度忽略不计).
例11.将一根长24
cm的筷子,置于底面直径为5
cm、高为12
cm的圆柱形水杯中,如图①~③所示,设筷子露在杯子外面的部分的长为h,则h的取值范围是什么?
1、勾股定理:
直角三角形两直角边a,b的平方和等于斜边c的平方,即a2+b2=c2。
2、勾股定理的逆定理:
如果三角形的三边长a,b,c有关系a2+b2=c2,那么这个三角形是直角三角形。
3、勾股数:
满足a2+b2=c2的三个正整数,称为勾股数。
若是勾股数组,则na、nb、nc也是勾股数组。
4、简单运用:
⑴勾股定理——常用于求边长、周长、面积;
理解:①已知直角三角形的两边求第三边,并能求出周长、面积。
②用于证明线段平方关系的问题。
③利用勾股定理,作出长为的线段
⑵勾股定理的逆定理——常用于判断三角形的形状;
理解:①确定最大边(不妨设为c);?
②若c2=a2+b2,则△ABC是以∠C为直角的三角形;?
若a2+b2<c2,则此三角形为钝角三角形(其中c为最大边);
?
若a2+b2>c2,则此三角形为锐角三角形(其中c为最大边)
考点:最短距离及相关问题
例1.
(2017立达期中)如图,一个高16m,底面周长8m的圆柱形水塔,现制造一个螺旋形登梯,为了减小坡度,要求登梯绕塔环绕一周半到达顶端,问登梯至少多长?
例2.(2017吴中区期中)如图,一圆柱高8
cm,底面半径为2
cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是(▲)
A.20
cm
B.10
cm
C.14
cm
D.无法确定
例3.(2017常熟期中)如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值_________.
例4(2018青云中学)如图,A村到公路L的距离AB为6
km,C村到公路
L的距离CD为2km,且BD的长为6
km.现要在公路
上取一点P,使AC+CP的值最小,则这个最小值
为
.
例5:如图,A、B两个小集镇在河流CD的同侧,到河的距离分别为AC=10千米、BD=30千米,且CD=30千米,现要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万元,请你在河流CD边上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用.
例6:“数学建模”
(1)模型——小马喝水问题:直线MN表示一条河流的岸,在河流同侧有A、B两地,小马从A地出发到B地,中间要在河边饮水一次,请在图①中用直尺和圆规作出使小马行走最短路程的饮水点P的位置.(作在答题纸上,保留作图痕迹,并用黑水笔将痕迹描深)
(2)运用——和最小问题:如图②,E是边长为8的正方形ABCD边BC上一点,CE=2,P是对角线BD上的一个动点,求PC+PE的最小值.
例7如图,长方体的长为15,宽为10,高为20,点B到点C的距离为5,如果一只蚂蚁要沿着长方体的表面从点A爬到点B,那么它需要爬行的最短距离是
(
)
A.5
B.25
C.15
D.35
例8如图,是一个三级台阶,它的每一级的长、宽、高分别为20dm、3dm、2dm,A和B是这个台阶两相对的端点,A点有一只昆虫想到B点去吃可口的食物,则昆虫沿着台阶爬到B点的最短路程是
分米。
例9.如图,一圆柱体的底面周长为20cm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,试求出爬行的最短路程.
例10
如图,一个圆柱形容器的高为1.2m,底面周长为Im.在容器内壁离容器底部0.3m的点B处有一只蚊子,此时一只壁虎正好在容器外壁离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为_______m(容器厚度忽略不计).
例11.将一根长24
cm的筷子,置于底面直径为5
cm、高为12
cm的圆柱形水杯中,如图①~③所示,设筷子露在杯子外面的部分的长为h,则h的取值范围是什么?
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
